三捷联惯组冗余系统故障检测阈值设计方法①

王易南，陈 康，闫 杰

(1．北京宇航系统工程研究所，北京 100076;2．西北工业大学 航天学院，西安 710072)

0 引言

捷联式惯导系统(Strap-down Inertial Navigation System)是把惯性仪表直接固联在载体上，用计算机来完成导航电子平台功能的惯性导航系统。在SINS中，惯性组件(陀螺仪和加速度计)是导航与控制系统的关键部件，通常是控制系统中容易发生故障的部分并易受不良环境的影响。因此，惯导系统的故障检测与诊断设计是提高可靠性的一种重要手段。

故障检测与诊断所采用的方法主要有基于硬件冗余的诊断法［1－2］、基于解析冗余的诊断法［3－4］、基于知识的诊断法［5］和基于信号处理的诊断法［6］。其中，基于硬件冗余的诊断法是最早也是目前最有效的一种诊断方法。在该方法中，对于故障阈值的计算是一项关键技术，最常用的方法是广义似然比方法(GLT)［7］。此外，还有基于构造测量值统计量的均值检验法［8］和基于样本加权的均值检验法［9］。

本文从工程角度出发，基于实际的惯组平台进行动态阈值的设计方法研究，并对其故障诊断效果进行了分析。

1 研究对象

本文研究的3套捷联惯组采用共支架，共基准的安装方式，由6个光纤惯组与3个激光惯组构成，如图1所示。

图1 3套惯组同轴安装示意图Fig．1 Coaxially mounted IMUs

2 惯组误差模型

2．1 陀螺误差模型

陀螺器件的误差模型可表示为

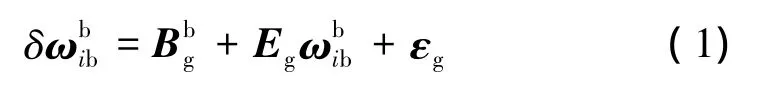
即

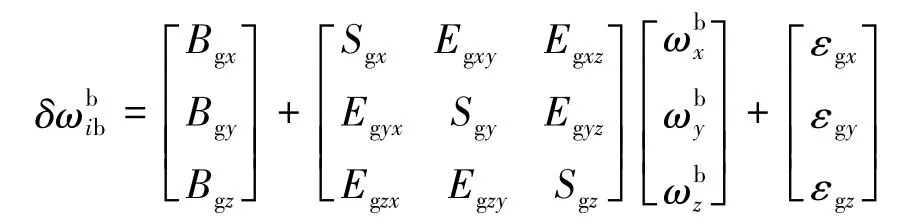
2．2 加速度计误差模型

加速度计器件的误差模型可表示为

即

3 三捷联惯组动态阈值设计

当惯组器件输出形式为脉冲时，2个器件输出之间的差值一定是脉冲的整数倍，就意味着只要2个器件的输出值不一样，它们之间的差值就会超出阈值，这显然不符合实际。因此，当器件以脉冲形式输出时，只能采用均值法进行阈值设计。

3．1 数据窗均值法

具体实施步骤:

(1)采用蒙特卡洛打靶生成脉冲输出值(如生成1 000条弹道的陀螺和加速度计的脉冲输出)。

(2)将同一物理量的3个传感器各时刻输出值P1j(t)、P2j(t)、P3j(t)两两相减，得到 3个差值序列，生成 x1=P1j(t)－P2j(t)，x2=P2j(t)－P3j(t)，x3=P1j(t)－P3j(t)的差值数据，采用kolmogorov-smirnov检验法对其进行检验，发现此时数据不服从正态分布，且无法详细地获取其分布状态。以x1为例，{x1(t)，x1(t+t0)，…，x1(t+(N－1)t0)}同分布，由中心极限定理可知，当N足够大时服从正态分布。

(3)选择数据窗长度N(如N=1 000)，以连续N个数据xi(tk－N+1)，…，xi(tk)的平均值为系统故障检测数据。

连续N(1 000)个数据的选取方法如图2所示。

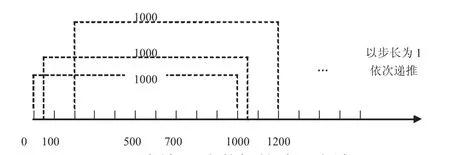
图2 连续N个数据的选取方法Fig．2 Method to select continuous data

3．2 分位数法阈值置信区间估计

通过kolmogorov-smirnov正态分布检验法进行数据检验，对于不服从正态分布的样本，需要确定其大致的分布状态。

对样本数据进行升序排序，将相同的数值合并，计算每一个数据在原样本数据中出现的次数占整体数据的比例，得到每个样本数据的出现概率。

在第一个窗长度以内的某一个时刻，找出平均数量比较小的一组样本，由于其累积次数不足，信息量不够大，但能反映出数据的大致分布规律，其概率分布图如图3所示。结合图3分析数据，发现样本数据依然较为规则地分布于0的两侧，小样本(绝对值)出现的概率大，大样本(绝对值)出现的概率小。结构相似于正态分布，但由于样本量较小，无法精确判断其结果。

在取出第一个窗长度后的对不服从正态分布的样本，计算其样本分布概率如图4所示。结合图4分析数据，此样本依然规则地分布于0值附近，大样本(绝对值)出现的概率大，小样本(绝对值)出现的概率小，类似于正态分布，但未通过严格的正态分布测试。

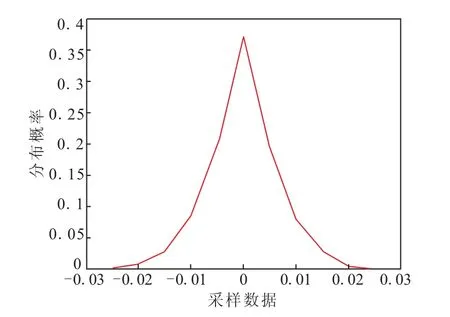
图3 第一个窗口长度内数据概率分布图Fig．3 Probability distributions of the data in the first window

图4 从第二个窗口开始数据概率分布图Fig．4 Probability distributions of the data in the second window

针对于这种特殊的情况，采用P分位数的方法来计算阈值，假设当前的置信度为1－α。求解置信区间时，需要求出的区域能最大限度地占据数据出现可能性最大的区域。针对于当前样本数据概率对称分布的状态，对称分配 2 个 P 分位数 Pα/2和 P1－α/2，通过此两点确定出置信上下界。

3．3 正态分布法阈值置信区间估计

对数据窗均值法处理后的数据，若其服从正态分布，均采用正态分布法进行置信区间的估计。

总体 X 服从正态分布 N(μ，σ2)，其中［X1，…，Xn］T为来自总体的一个样本μ、σ未知，使用最大似然估计的方法估计出μ和σ的值得到总体X正态分布的分布密度为

置信上界up满足:^

故x的置信度为1－α的置信区间为

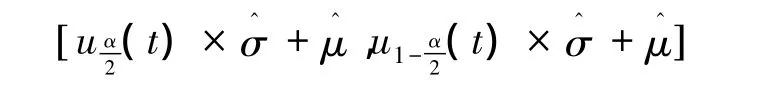
3．4 阈值分段设计

(1)将通过概率统计法得到的阈值，按时间变化逐序进行差分，即可判断出其各个时刻点数据阈值的变化情况;

(2)选择其变化率最大的时刻点为分段点，然后分析各时间段的阈值数据，取其最大最小值分别作为此时间段的阈值上下限。

以惯组1和惯组2在X轴方向上的绕质心旋转角速度脉冲值差值为例，其阈值变化曲线如图5所示。惯组1和惯组2在X轴方向上的绕质心旋转角速度脉冲值差值变化曲线有11个很明显的拐点，此处其变化率最大，对此数据求解一阶导数，如图6所示，取其变化率最大的点为阈值分段点，然后分析各个分段区间内的数据变化，取此段区间的最大最小值分别为此段区间的阈值上下限，则分段后的阈值上限变化曲线如图7所示。

4 三捷联惯组故障检测方法

故障诊断方法采用门限表决方法，其主要流程如下:

(1)在运载火箭飞行过程中，实时测量同一物理量的3个传感器测量值 P1j(t)、P2j(t)、P3j(t)，计算P1j(t)－P2j(t)，P2j(t)－P3j(t)，P1j(t)－P3j(t)值，并判断其是否落入置信区间内。

当P1j(t)－P2j(t)落入置信区间，记 ε1=1，否则记ε1=0;

当P2j(t)－P3j(t)落入置信区间，记 ε2=1，否则记ε2=0;

当P1j(t)－P3j(t)落入置信区间，记 ε3=1，否则记ε3=0。

(2)当ε1+ε2+ε3=2时，判断传感器未出现故障。取惯组1输出量为惯导输出量，进行惯导解算。

(3)当 ε1+ε2+ε3=1，则可依据服从多数原则，判定一个传感器发生了故障，即判断出现1°故障。

当ε1=1时，判断惯组3传感器故障，取惯组1输出量为惯导输出量进行，惯导解算;

当ε2=1时，判断惯组1传感器故障，取惯组2输出，为惯导输出量进行，惯导解算;

当ε3=1时，判断惯组2传感器故障，取惯组1输出量为惯导输出量进行，惯导解算。

(4)当 ε1+ε2+ε3=0 时，判断出现 2°故障。这种情况需要进一步研究，可依据传感器信号输出的频域特性、基准弹道指令等辅助手段来进行故障判断。

图5 阈值变化曲线Fig．5 The threshold curve

图6 阈值变化率曲线Fig．6 The rate of threshold changing

图7 分段后的阈值上限变化曲线Fig．7 The upper limit curve

5 检测结果及分析

故障模型主要包括输出故障和参数故障:参数故障是指(零次项、标度因数等)变化引起的突变和线性、正弦、方波漂移的缓变故障;输出故障是包括常零值、满量程及倍频率输出。

本文以对IMU3在Z轴上的陀螺注入零次项参数方波故障为例，其开始注入故障时刻为20 s时，故障幅值分别为 5、10、20、50、100°/h，频率分别为1、5、20 Hz，仿真100次，检测结果如图8所示。

图8 统计置信水平α为0．05和0．002时的仿真结果Fig．8 Simulation results when the confidence level is 0．05 and 0．002

由图8可见，将统计置信水平 α=0．05和 α=0．002条件下的仿真结果相比较:前者最早检测到故障时间和平均检测到故障时间比后者相对早一些，随着注入故障幅值的增大，其最早检测到故障时间和平均检测到故障时间都逐渐缩短，但随着注入故障频率的增大，其最早检测到故障时间和平均检测到故障时间会逐渐增长;前者误警率明显升高，其误警率约在3%～5%之间，而后者的误警率为0%。然而，两者的误警率都严格控制在5%的范围内，漏警率均为0%，完全满足本次仿真的指标要求。

6 结论

(1)针对共支架、共基准方式安装的三捷联惯组冗余系统，建立了陀螺和加速度计的误差模型，进行了蒙特卡洛仿真并量化处理，得到了3套陀螺和加速度计的脉冲输出。

(2)惯组器件的脉冲当量对惯组冗余系统的阈值区间的分布有较大影响，脉冲当量越小，阈值区间的分布越趋近于标准正态分布。在脉冲当量较大的情况下，部分阈值区间不服从正态分布，但可通过分位数法进行解算。

(3)使用数据窗均值法得到的阈值区间能够反映出载体机动对惯组系统阈值的影响，根据阈值的变化率，可动态地计算分段阈值。

(4)根据此方法计算的阈值能够有效地检测到三捷联惯组中发生故障的陀螺或加速度计，且检测到故障时间、漏警率和虚警率均满足指标要求。

［1］ 王仲生．职能故障诊断与容错控制［M］．西安:西北工业大学出版社，2005．

［2］ 吴今培．职能故障诊断技术的发展与展望［J］．振动、测试与诊断，1999(2):79-86．

［3］ 吴今培，肖建华．智能故障诊断与专家系统［M］．北京:科学出版社，1997:1-77．

［4］ Umar Iqbal Bhatti，Washington Yotto Ochieng．Failure modes and models for integrated GPS/INS systems［J］．The Journal of Navigation，2007，60:327-348．

［5］ Umar I Bhatti，Washington Y Ochieng，Shaojun Feng．Integrity of an integrated GPS/INS system in the presence of slowly growing errors［J］．GPS Solut ，2007，11:173-181．

［6］ 张玲霞．导航系统故障检测与诊断及其相关理论问题的研究［D］．西安:西北工业大学，2004．

［7］ 潘鸿飞，任尚云，袁立群．捷联惯导系统故障检测与处理技术研究［J］．上海航天，2002(6):37-39．

［8］ 钱华明．故障诊断与容错技术及其在组合导航系统中应用研究［D］．哈尔滨:哈尔滨工程大学，2004:80-86．