不同膨胀状态下拉瓦尔喷管内耦合传热数值研究①

刘 锐，陈 雄，周长省，李映坤

(南京理工大学机械工程学院，南京 210094)

0 引言

喷管是火箭发动机能量转换的重要部件，它把高温高压燃气的热能和压强势能转变为高速排出的气体动能，产生反作用力。当喷管的扩张比给定时，根据喷管入口与出口反压之比NPR(nozzle pressure ratio)的不同，喷管的工作状态可分为过膨胀状态、最佳膨胀状态和欠膨胀状态［1］。

火箭发动机喷管在工作过程中，可能会经历上述多种膨胀状态。例如，火箭在不同高度的空域飞行或发动机工作的开始及结束阶段，外界反压或燃烧室内压力会发生很大变化，此时喷管会处于过膨胀状态，并可能产生流动分离［2－4］，流动分离会加剧分离点处的传热及烧蚀［5－6］。通常情况下，喷管尺寸依据最佳膨胀状态而设计，但由于多级推力在实际应用中的需求(如单室多推力、多级火箭等)，燃烧室内的工作压强是变化的，在火箭工作的部分时间内，喷管会处于欠膨胀状态，在最佳膨胀状态或欠膨胀状态下，喷管壁面不会出现流动分离。对喷管壁面无流动分离情况下的传热研究，国内外学者也做了很多工作。其中，耦合传热被证明是一种能准确预示喷管固壁材料内部及边界上温度和热流密度分布的方法［7－11］，可为喷管热防护设计提供可靠依据。

目前，关于喷管在不同膨胀状态下连续转变过程中，其壁面传热特性及内部流场结构的研究报道较少，而实际工作中的喷管可能经历由过膨胀状态到欠膨胀状态的转变。本文将N-S求解程序中速度相关项设为零，应用于固体区域热传导求解，流固界面处保证热流密度连续实现耦合传热，流体和固体区域的求解只使用1套程序，这样可省去2套不同程序，甚至第3个数据传输程序的编写，提高效率［12］。验证该程序后，以文献［13］中的喷管为例，研究在外界反压已定的情况下，通过改变入口压力，使喷管处于不同膨胀状态时，其壁面传热特性及流场结构，为相关设计提供参考。

1 控制方程及数值求解方法

1．1 控制方程

1．1．1 流场控制方程

二维轴对称积分形式的可压缩非定常Navier-Stokes方程的形式如下所示:

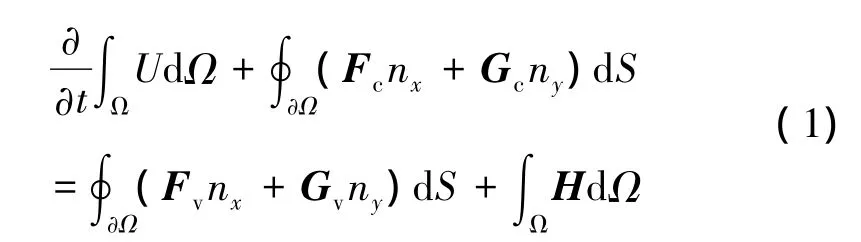
式中 U为守恒变量;(Fc，Gc)和(Fv，Gv)分别为对流通量和粘性通量;H为轴对称几何源项。

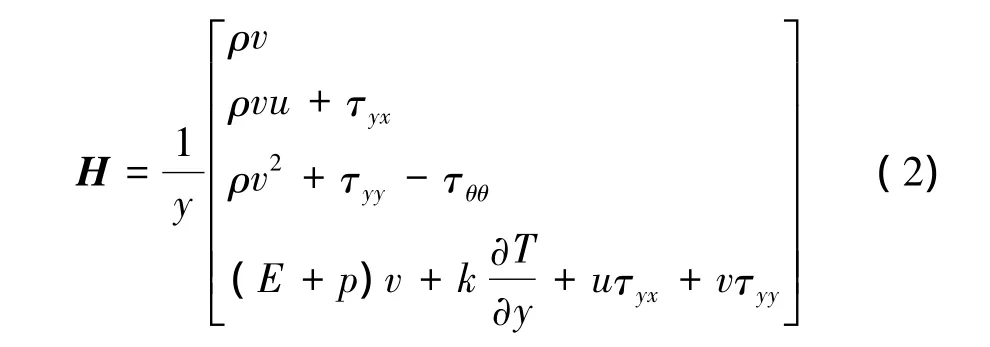
其中

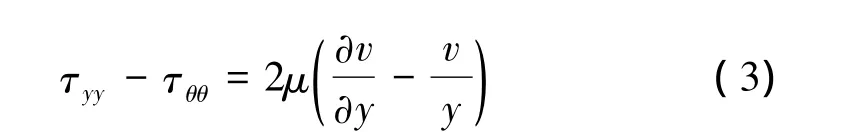
湍流模型采用 Menter提出的 k-ω SST(shearstress-transport)模型［14］。

1．1．2 固体热传导控制方程

固体区域中不存在对流，热量通过扩散的形式传递，该过程本质上与流体中的能量扩散一致。所以，将N-S方程中与速度及其偏导数相关的对流通量设为零，便可用于求解固体区域的热传导过程，将控制方程写为类似于方程(1)的形式:

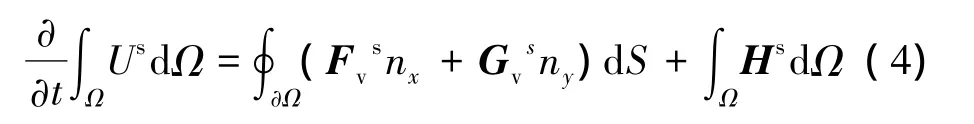
其中

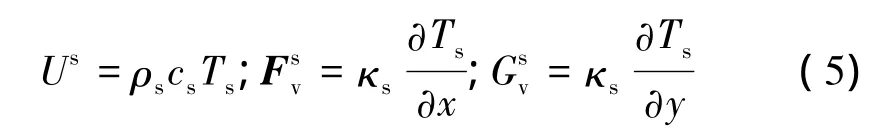
轴对称源项:

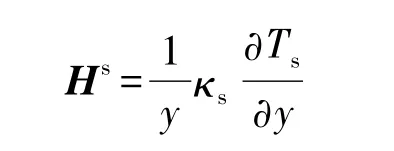
1．2 数值计算方法

在求解N-S方程中，本程序所使用的数值计算方法概括如下:

对流项的离散采用具有保单调性的三阶MUSCL格式［15］，网格单元界面处采用原始变量(密度、速度、压力)进行重构，重构方法选取 AUSM-PW 格式［15］。粘性项的离散采用具有二阶精度的中心差分格式，粘性应力张量和粘性通量中的偏导数项采用Jacobian变换来计算［15］。时间推进采取LU-SGS隐式算法，并使用局部时间步长加速收敛技术。

固体区域热传导方程求解的关键是网格界面上热流密度的计算。热传导方程中，扩散项(热流密度)的离散方法与N-S方程中粘性项的离散方法一致，均采用空间上具有二阶精度的中心差分格式，扩散项中温度的偏导数采用Jacobian变换来计算。

1．3 耦合传热

通过保证固体区域和流体区域界面上热流密度连续，实现耦合传热。耦合界面处流场区域的热流密度的计算方法如下所示:

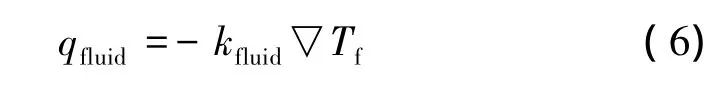
耦合界面处固体区域的热流密度qsolid计算方法如下所示:

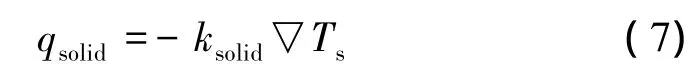
通过式(8)保证耦合界面处热流密度连续:

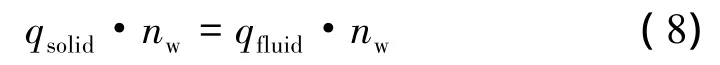
耦合传热的具体步骤如下:

(1)初始化流场和固体场，通过式(6)～式(8)求出耦合边界上的温度分布Tw，该温度满足在耦合界面上热流密度连续的约束条件。

(2)将耦合界面上的温度分布Tw作为边界条件，对流场区域和固体区域进行推进求解，更新耦合界面处流场和固体场格心处的变量。对于瞬态问题而言，流场区域和固体区域推进时间步长应一致，可采用双时间步推进;对于稳态问题而言，为加快定常解的收敛速度，流场区域和固体区域，可选用不同的推进时间步长。

(3)利用更新后的格心处的参数，通过上式求出耦合边界上新的温度分布Tw，重复步骤(2)，直至收敛。

2 程序验证

以文献［13］中的喷管为例，对本程序进行验证。Back L H等对一轴对称收敛-扩张型喷管内对流换热规律进行了实验研究。高压空气通过酒精燃烧加热，经过一截面积恒定的圆管后进入喷管。喷管喉部直径为 0．045 8 m，收敛比为 7．75 ∶1，扩张比为 2．68 ∶1，收敛半角和扩张半角分别为30°和15°。喷管的网格及边界条件如图1所示，为了准确捕捉近壁面的流动传热特性，喷管入口处和出口处的第一层网格到壁面的距离分别为 2×10－6m 和 1×10－6m，使得 y+沿整个喷管都小于 0．5。

实验中喷管外壁面由流动水冷却，计算中设为等温壁，其温度分布数据取自文献［12］。喷管壁面材料的密度为7 750 kg/m3、比热容为460 J/(kg·K)、热导率为36．67 W/(m·K)。喷管入口的总温T0为840 K、总压 p0为 1．752 MPa、燃气的比热比为 1．35。

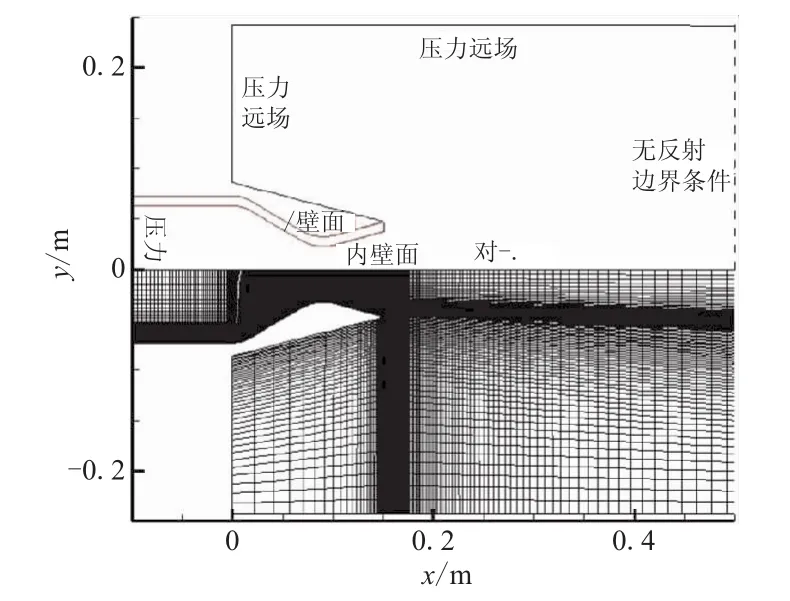
图1 网格及边界条件Fig．1 Mesh and boundary conditions

对喷管及壁面进行耦合求解，耦合壁面处的对流换热系数h可通过下式求得:

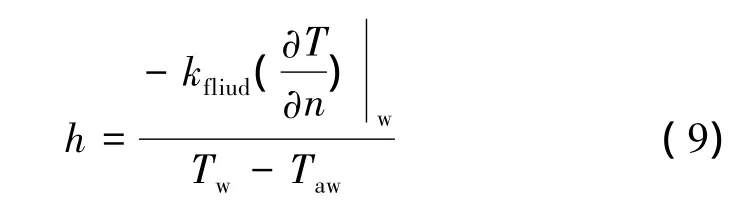
其中，Tw为壁面处的温度;Taw为恢复温度，可通过下式求得

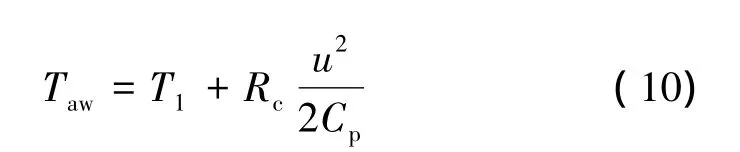
式中 Rc为恢复因子，Rc=0．89［16］;T1和 u 分别为喷管轴线处的静温和速度。

计算所得的对流换热系数与实验所测数据如图2所示。从图2可看出，本文所编制的耦合传热程序计算出的结果与实验所测数据相符，说明了本文所编制耦合传热程序的有效性。

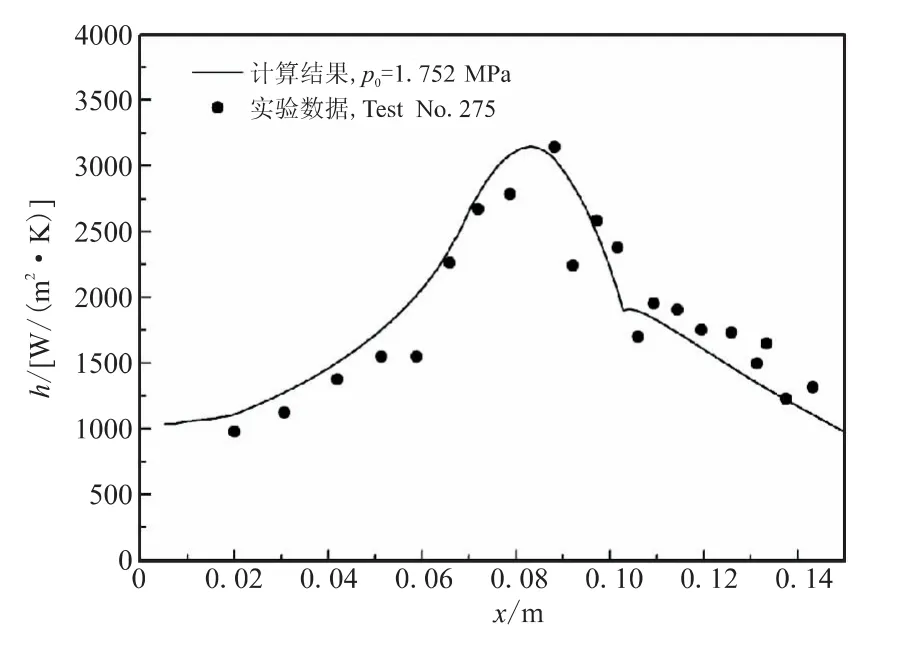
图2 对流换热系数计算结果与测量结果比较Fig．2 Comparison of calculated and measured heat transfer coefficients

3 计算结果及讨论

本章计算采用的模型仍为算例验证中所用的喷管，只改变其入口总压，其他边界条件保持不变，用来模拟研究该喷管在过膨胀-最佳膨胀-欠膨胀变化历程中，喷管内流场以及壁面的传热特性。研究内容分为稳态过程和动态过程。

稳态过程研究中，入口总压 p0分别取 0．38、0．45、1．65、1．752、5、7 MPa，这种情况下，关心的只是稳定状态下的定常解。所以，为加速收敛过程，流场区域和固体区域选取不同的推进时间步长。

动态过程研究中，入口总压设定为随时间线性增大，其变化规律为 p0=(0．924t+0．38)MPa。这种情况下，流场区域和固体区域选取相同的推进时间步长10－5s。

3．1 稳态过程结果分析

3．1．1 流场结果分析

图3为不同入口总压条件下的马赫数云图。当入口总压为0．38 MPa和0．45 MPa时，喷管处于过膨胀状态。由图3可看出，在喷管的扩张段壁面出现了流动分离，分离点处产生了一道斜激波。在喷管轴线处会产生一道正激波，流动在此由超音速(激波前)变为亚音速(激波后)。当入口总压为1．65 MPa和1．752 MPa时，喷管壁面处未出现流动分离，喷管出口产生马赫盘。入口总压为5 MPa和7 MPa时，不会产生流动分离，流场结构与总压取1．65 MPa和1．752 MPa时类似。

图4为不同入口总压条件下，喷管壁面处的压力分布。从图4可看出，在壁面有分离的情况下，分离点的位置与喷管入口处的压力有关。当入口总压为0．38 MPa时，分离点的位置在 x=0．125 m 处;当入口压力增加到0．45 MPa时，分离点的位置向喷管外侧移动至x=0．133 m处，分离点后，壁面压强逐渐升高至出口处的环境压力。对于壁面未出现分离的情况(入口总压为 1．65、1．752、5、7 MPa)而言，喷管壁面处的压力沿流动方向呈现单调递减的趋势。

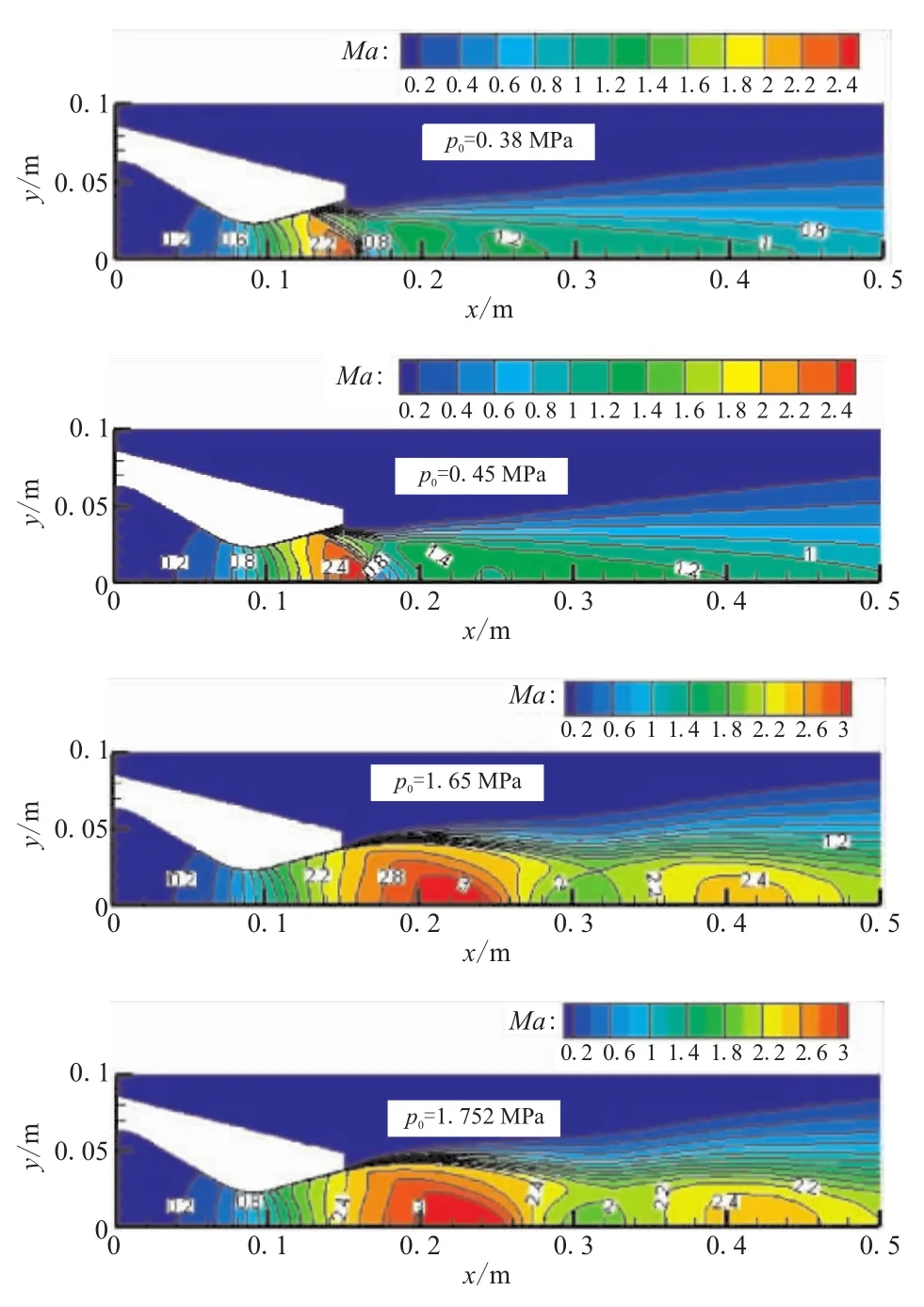
图3 不同总压条件下马赫数云图Fig．3 Mach contour for different total pressures

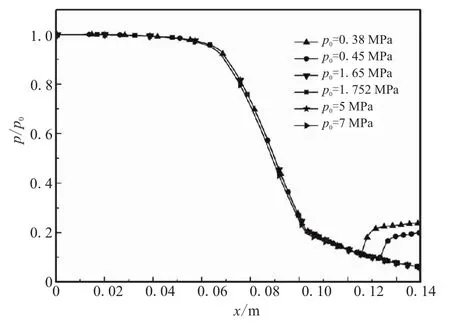
图4 喷管壁面的压力分布Fig．4 Pressure distribution along the nozzle surface

3．1．2 耦合传热结果分析

图5为不同入口总压条件下，喷管内的流场及固体壁面在达到稳态时的温度分布。如图5(a)和图5(b)所示，当入口总压力为 0．38 MPa和 0．45 MPa时，其主流区的温度沿流动方向逐渐降低，在扩张段内的斜激波处，温度会升高，这是由于此处斜激波的存在，使燃气速度降低(如图3所示)，致使温度升高。这两种工况下，壁面处均会产生流动分离，外界空气在反压的作用下会流入喷管内部，致使分离点过后，喷管壁面附近流场的温度较低。从喷管固体壁面内部温度分布可看出，最高温度出现在喉部附近，分离点后，喷管接触的是外界常温空气，致使该区域温度较低。

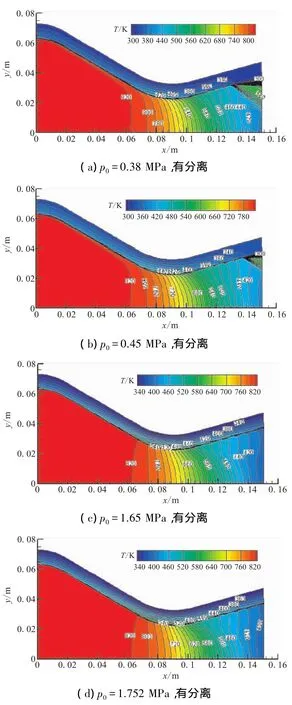
图5 不同总压条件下流体及固体区域的温度分布Fig．5 Temperature distribution of the fluid and solid domains for different total pressures

图 5(c)和(d)分别为喷管入口总压取 1．65、1．752 MPa时所对应的温度分布云图。这两种工况下，喷管未出现流动分离的情况，整个喷管中流动均为膨胀加速的(如图3所示)，喷管主流区的温度沿流动方向逐渐减小。对固体壁面而言，最高温度仍然出现在喉部附近与燃气接触的表面，从喷管壳体内表面(wall-in)到外表面(wall-out)，温度均呈递减趋势。入口总压为5、7 MPa时，不会产生流动分离，流场和固体区域的温度变化规律与总压取 1．65、1．752 MPa 时类似。

3．1．3 壁面对流换热分析

当喷管壁面处没有流动分离时，可用式(10)计算出恢复温度，并得到相应的对流换热系数。然而，对于存在分离流动的喷管而言，流场中温度会出现阶跃性的变化(如图5(a)和(b)所示)，式(10)将不再适用。所以，下文关于对流换热的讨论中，以热流密度为准，其计算公式为，并规定当热量从流体传向固体时，热流密度为正。

图6为喷管内流场与固体壁面耦合传热达到稳定状态时，耦合壁面处的热流密度的分布。从图6中可看出，对于入口总压为 0．38、0．45、1．65、1．752、5、7 MPa这几种情况而言，热流密度都是沿流动方向呈现先增加后减小的趋势，最大值分别为 0．434、0．48、0．796、0．825、1．244、1．331 MW/m2，均出现在喉部上游位置，随着入口总压从0．38 MPa增加到7 MPa，热流密度呈增大的趋势。这是因为当燃烧室压力升高时，质量流率就会增大，流动的雷诺数也会随之增大，进而引起喷管内对流换热的增强。

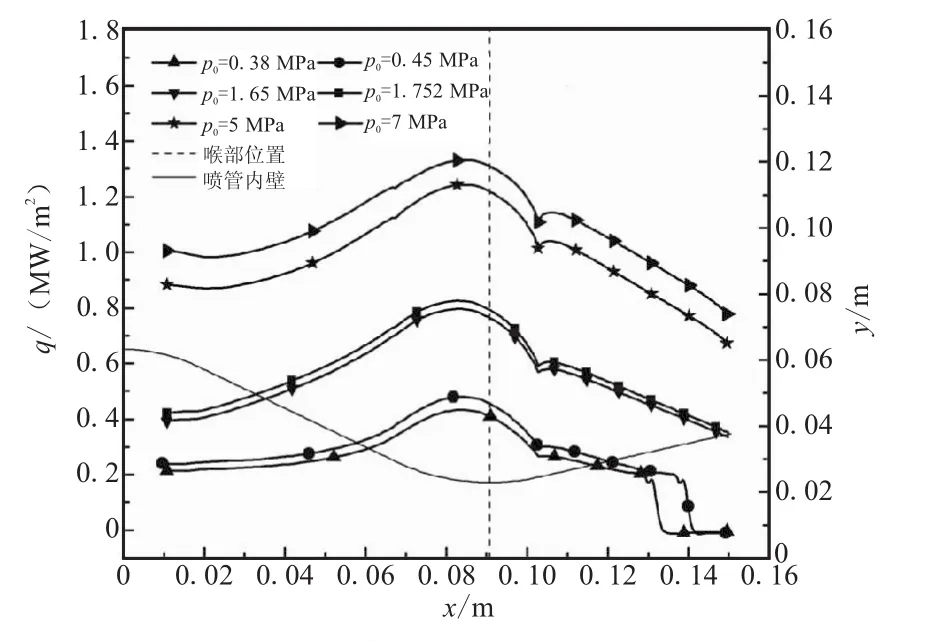
图6 耦合壁面热流密度分布Fig．6 Heat flux distribution along the coupled wall

当喷管内存在流动分离时(入口总压为0．38 MPa和0．45 MPa)，分离点处的热流密度先突然升高，然后急剧下降，该现象是因为在分离点的处，气体的流动参数发生了很大变化，同时分离点处斜激波两侧气体为高温燃气和常温空气，它们的热物性也有一定差别，导致了分离点处的对流换热会突然抬升。分离点过后，热流密度变为负值均在－0．001 MW/m2左右，说明此处气体冷却与之接触的壁面，这是因为在热传导的作用下，热量会从分离点上游区域的高温壳体，传递到分离点下游温度较低的区域(如图5(a)和(b)所示)，而与分离点下游壁面接触的是外界反压作用下流入喷管内的常温空气，而且此处空气流速较低(如图3所示)，这就导致了此处热流密度为负值且绝对值较低。

图7给出的是耦合壁面在稳态时的温度分布。从图7可看出，耦合壁面处的温度分布与热流密度的分布规律相似，沿流动方向先增大后减小，在喉部上游达到最大值，喷管入口总压为 0．38、0．45、1．65、1．752、5、7 MPa时，所对应的壁面温度最大值分别为448．2、462．1、560．7、570．1、698．1、726．7 K。当入口压力为 0．38 MPa和0．45 MPa时，温度并没有像其对应的热流密度那样，在分离点附近出现突然抬升的现象。这是因为喷管壁面的热传导作用，使得热量从温度较高的上游壳体传递到温度较低的下游壳体，而且本文所计算的工况下，分离点处热流密度的抬升幅度较小(与喷管的几何构型和流动参数有关)，这也导致壁面温度没有出现突然升高的现象。

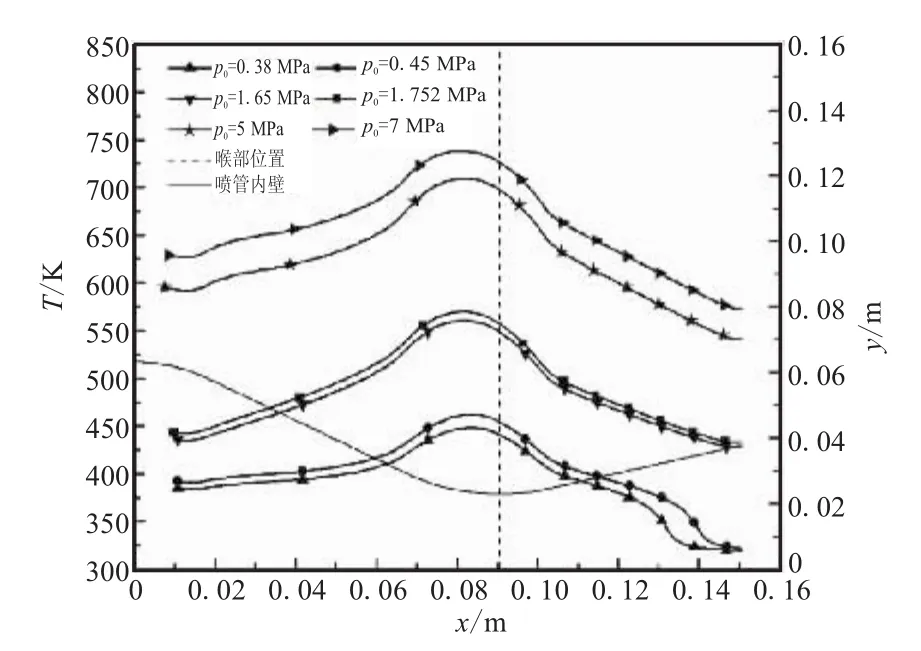
图7 耦合壁面温度分布Fig．7 Temperature distribution along the coupled wall

3．2 动态过程分析

为研究入口总压随时间变化时，喷管流动分离的动态过程和热流密度的动态变化过程。入口总压设定为随时间线性增大，其变化规律为p=(0．924t+0．38)MPa。

图8为t=0～0．5 s内，壁面压力的动态变化规律，图中给出曲线的时间间隔为0．05 s。当t=0 s时，喷管会产生流动分离，随着入口总压的不断增大，分离点不断后移;当 t=3．5 s时，入口压力升高至 0．703 MPa，此时喷管内不再产生流动分离，压力沿壁面呈单调递减趋势。

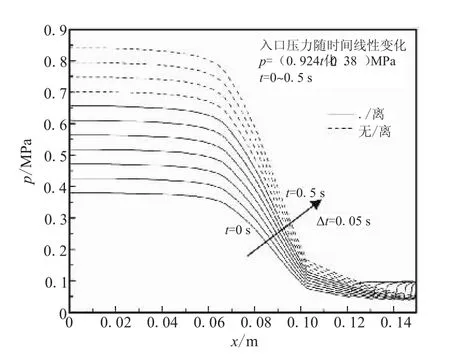
图8 不同时刻壁面压力的分布Fig．8 Pressure distribution at different time

图9为耦合壁面上热流密度的动态变化过程。当入口压力随时间增大时，对流换热强度会随时间增强，热流密度沿壁面的分布规律与稳态解基本一致，但在动态分离过程中，分离点处的热流密度没有呈现先突然升高、后急剧下降的规律(如图6所示)。这可能是因为入口压力随时间不断变化，使得分离点的动态移动过程中，分离点壁面附近流场不能达到一稳定状态，进而影响到与壁面的对流换热。

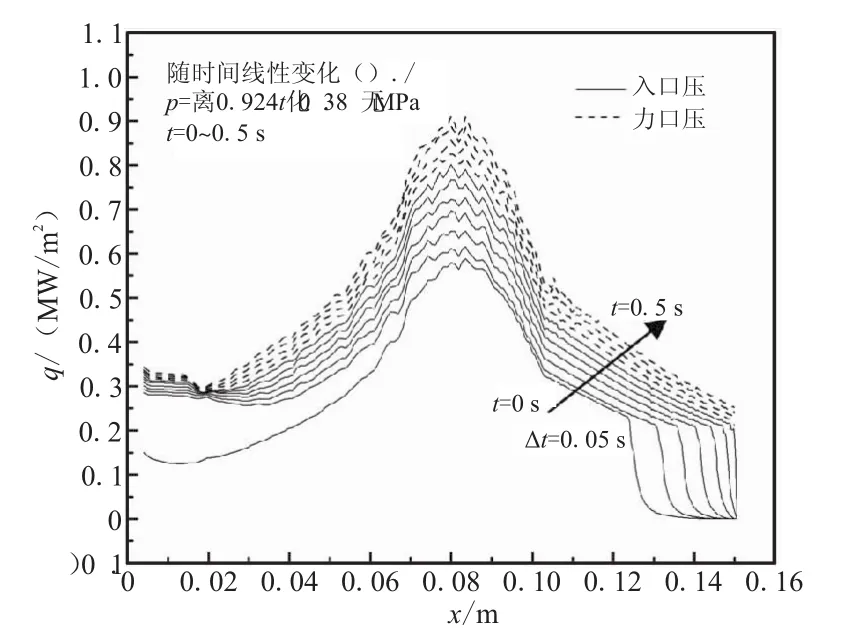
图9 不同时刻热流密度的分布Fig．9 Heat flux distribution at different time

4 结论

(1)喷管在各种膨胀状态下，其壁面处热流密度都是沿流动方向先增大后减小，在喉部上游达到最大值，对流换热强度会随着喷管入口总压的增大而加强。

(2)对于喷管壁面存在流动分离的情况而言，热流密度在分离点处会突然升高。这是由于此处斜激波的存在，导致流场参数发生剧烈变化，引起分离点当地的对流换热会增强，这种变化规律在动态分离过程中没有出现。分离点过后的大部分区域内气体是对喷管壁面进行冷却，但对流换热强度较低。

［1］ 武晓松，陈军，王栋．固体火箭发动机原理［M］．北京:兵器工业出版社，2006．

［2］ 孙得川，李江，蔡体敏，等．影响喷管流动分离的因素［J］．推进技术，2000，21(2):19-21．

［3］ Xiao Q，Tsai H M，Papamoschou D．Numerical investigation of supersonic nozzle flow separation［J］．AIAA Journal，2007，45(3):532-541．

［4］ 王艺杰，鲍福廷，杜佳佳．固体火箭发动机喷管分离流动数值模拟及试验研究［J］．固体火箭技术，2010，33(4):406-408．

［5］ 胡海峰，鲍福廷，王艺杰，等．喷管分离流流动-热结构顺序耦合数值模拟及试验研究［J］．宇航学报，2011，32(7):1534-1541．

［6］ 吴朋朋，杨月诚，高双武，等．固体火箭发动机喷管分离流动流固耦合数值仿真［J］．固体火箭技术，2012，35(3):344-347．

［7］ 张晓光，王长辉，刘宇，等．固体火箭发动机喉衬流场及热结构耦合分析［J］．固体火箭技术，2011，34(5):579-583．

［8］ 张兵，韩景龙．多场耦合计算平台与高超声速热防护结构传热问题研究［J］．航空学报，2011，32(3):400-409．

［9］ Eric R Perrell，Greg D Power，Chris Robinson．A modular conjugate heat transfer capability for the wind-US CFD code［R］．AIAA 2010-31．

［10］ Liu Q，Luke E A，Cinnella P．Coupling heat transfer and fluid flow solvers for multidisciplinary simulations［J］．Journal of Thermophysics and Heat Transfer，2005，19(4):417-427．

［11］ William Engblom，Bruno Fletcher，Nicholas Georgiadis．Conjugate conduction-convection heat transfer for water-cooled high-speed flows［C］//44th AIAA/ASME/SAE/ASEE Joint Propulsion Conference ＆ Exhibit，Hartford，CT，July 21-23，2008．

［12］ Schluter J U，Wu X，van der Weide E，et al．Multi-code simulations:a generalized coupling approach［R］．AIAA paper，2005:4997．

［13］ Back L H，Massier P F，Gier H L．Convective heat transfer in a convergent-divergent nozzle［J］．International Journal of Heat and Mass Transfer，1964，7:549-568．

［14］ Menter F R．Two-equation eddy-viscosity turbulence models for engineering applications［J］．AIAA Journal，1994，32(8):1598-1605．

［15］ Blazek J．Computational fluid dynamics:principles and applications［M］．Elsevier，2001．

［16］ Piyush Thakre．Chemical erosion of graphite and refractory metal nozzles and its mitigation in solid-propellant rocket motors［D］．Pennsylvania:The Pennsylvania State University，2008．