换轮减速箱齿轮副的优化和校核

杨 瑶，刘 阳，文 瑶，李 源，刘 浩

（湖北工业大学农业机械研究设计院，湖北 武汉430068）

为了满足南方丘陵水网地区土地狭小分散、水田旱地杂陈而设计的水陆两用机耕船，其重要的部件之一是用于转换水用叶轮和陆用胶轮的换轮减速箱。在工作中，换轮减速箱带动叶胶轮上下摆动，减速箱的体积过大，需要大量的预留工作空间，而且导致能量的浪费，以及水陆两用机耕船自身体积过大，而废材耗资，还会致使机耕船工作的灵活度下降。熊禾根、孔建益等避开常规的齿轮设计方法，提出一种基于遗传算法的交互式优化方法，大大节约了设计的时间和成本［1］；王得胜等人利用一种仿生学算法——蚁群算法对圆柱齿轮进行优化［2］；王占奎、薛春善等人将遗传算法与粒子群算法相结合，对圆柱齿轮进行优化设计和编程实现［3］；毛志伟通过对齿轮加工数据以及Reilhofer系统的振动数据的分析，进一步降低了传动误差，改善了变速器的噪音［4］。但是，所采用的遗传算法和仿生物算法过程都非常的复杂，计算过程并不方便，并且在工况相对简单的情况下工作量仍过大，而且不能满足特定的实际需求。

本文考虑的换轮减速箱工况并不复杂，在工作过程中时速相对较慢，对于力学性能的要求也不高，解决的问题是改善减速箱体积过大所造成的不便。根据工程结构优化设计［5］的理论基础，建立变速箱输出齿轮副体积为目标函数优化设计的数学模型，然后利用MATLAB的Optimization Toolbox优化工具箱，对其进行优化运算，最后通过圆整优化运算的结果得到齿轮副优化设计的各项参数。

1 优化设计数学模型的建立

要使得减速箱的体积在满足强度以及硬度等约束条件下达到最小，首先，在输出齿轮的设计过程中还应避免发生根切现象，在传动过程中不会发生干涉等几何条件的约束；其次，齿轮的其他相关优化设计变量也应该在约束条件的范围内考虑。由此可将优化设计的数学模型总结为一个多元的优化目标函数［6］，多个优化条件约束问题的表达式

其中，Vmin为齿轮副体积向量极小化

1.1 优化设计变量的确定

一个设计方案可以用一组基本参数来表示，这些基本参数可以是构建尺寸等几何量，也可以是质量等物理量，还可以是应力、变形等表示工作性能的导出量。在设计过程中选择并最终确定的各项独立基本参数，称作设计变量，又叫优化参数［7］。本文优化问题定义为有约束的多元单目标函数优化问题，需要选定一组参数来对优化的目标函数进行描述，对于齿轮副来说，可以改变的是它们的模数、齿数和齿宽，当这些被优化的参数当做变量确定下来以后，其他参数就可以被当做常量了。

齿轮副优化设计的基本参数为：齿轮的模数m、小齿轮的齿数z、小齿轮的齿宽系数φ1，以及大齿轮的齿宽系数φ2分别对应为x1、x2、x3和x4。所以，齿轮副的优化设计变量就可以被确定为

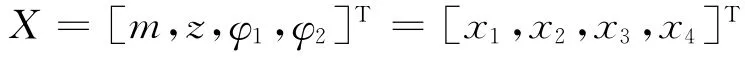
齿轮副的各项其他基本参数见表1，材料为20CrMnTi，功率P＝75kw，传动比i＝2.6，大齿轮转速1 000r／min。

表1 大小齿轮基本参数

1.2 建立优化设计的目标函数

优化设计的目标是在不改变输出齿轮副传动比，闭式齿轮必须满足避免齿轮点蚀、轮齿折断等基本条件下，尽量减小变速箱输出齿轮副的体积之和，从而使得换轮变速箱工作运转更为灵活且节约制造成本的目的，同时也可以使得齿轮副的传动更为平稳，减少噪音。由上述已定参数描述的换轮变速箱体积最小为优化目标的目标函数

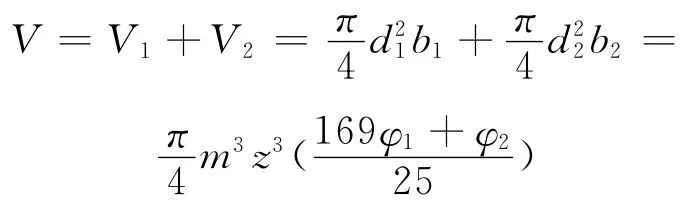
式中：V为体积之和；V1，V2为两啮合齿轮各自的体积；d1，d2为两啮合齿轮的直径；b1，b2为两啮合齿轮齿宽。

1.3 优化设计的约束条件

1.3.1 最小模数的约束条件 工业中常用齿轮的模数一般情况下不小于2，所以模数的约束方程为

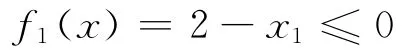
1.3.2 避免发生根切 用标准齿条刀加工齿轮时，若刀具的齿顶线与啮合线的交点和啮合极限点重合时，刚好不发生根切。经几何计算可以得出加工标准齿轮不发生根切的最小齿数，α＝20°时，zmin＝18［8］，所以不发生根切的约束方程是

1.3.3 齿宽系数的约束条件 对于工业用直齿圆柱齿轮，齿宽系数φ一般要求在0.2～0.5之间，齿宽系数的约束方程为

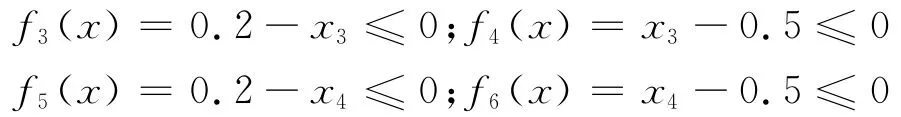
1.3.4 接触强度的约束条件 齿轮工作时，齿面间接触处将产生脉动循环的接触应力。在接触应力反复作用下，有可能会出现点蚀，从而影响正常工作使传动失效。

啮合齿轮齿面接触应力的平均应力

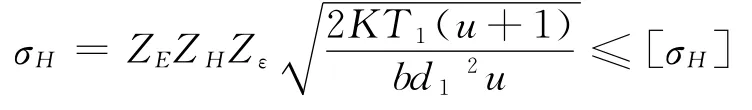
式中：ZE为材料的弹性系数；ZH为节点区域系数；Zε为重合度系数；u为传动比；K为载荷系数，K＝KAKVKβKα。查机械设计手册，将数据（表2）。代入参数，计算得

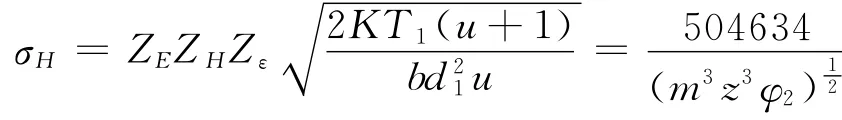
表2 相关参数数据

许用接触应力

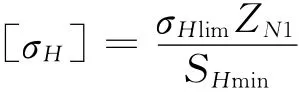
式中：SHmin为接触最小安全系数；ZN1为接触寿命系数；σHmin为接触疲劳极限；

查机械设计手册，将相关数据代入计算得

可得约束方程

1.3.5 弯曲强度约束条件 在齿轮传动工作时，齿轮相当于一个悬臂梁。承受载荷时，在其齿根部弯曲应力最大，且在齿根过渡圆角处有应力集中［8］。在此处的弯曲应力超过材料的弯曲疲劳极限，并在交变应力的多次作用下，会导致轮齿发生疲劳折断。为使其在工作寿命内不会发生疲劳折断的约束方程为

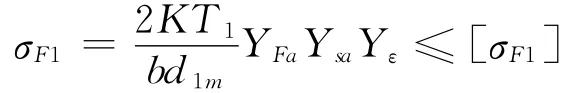
式中：YFa为齿形系数；Fsa为齿根应力集中系数；Fε为重合度系数；查询机械设计手册可以得到上述参数的值，代入后计算得

许用弯曲强度

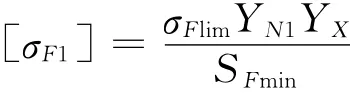
式中：σFlim为弯曲疲劳极限；YN1为弯曲寿命系数；SFmin为弯曲最小安全系数，所以

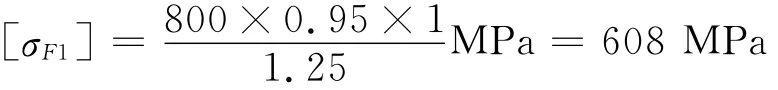
由上可得弯曲强度约束方程为

1.4 MATLAB优化工具箱优化

MATLAB工具箱中有许多基本函数可以调用求解最优化问题。选用了fmincon函数对体积函数做优化。函数优化的流程图如图1所示。

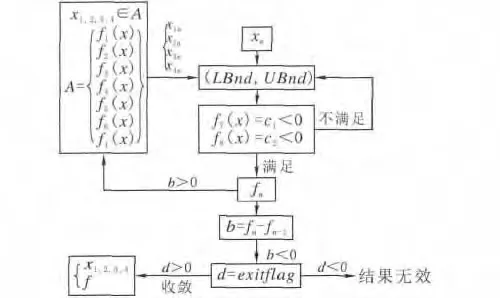
图1 程序流程图

函数fmincon调用格式如下：

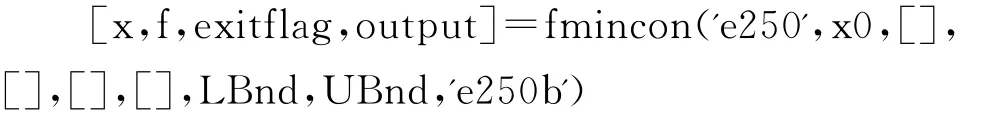
最后得到的计算结果整理到表3中。

表3 优化结果汇总表

经过圆整，得m ＝4，z＝18，φ1＝0.5，φ2＝0.2，其中exitflag＝1表示优化结果收敛于解。

优化后的齿轮传动的体积

优化前的齿轮传动的体积

所以，优化后体积减小了21.89%。

2 有限元软件检验齿轮副力学性能

ANSYS软件对啮合齿轮进行有限元分析得出的结果是符合实际工况且合理可靠［9］。优化后得到的小齿轮参数为m ＝4，z1＝18，φ1＝0.5，z2＝47。代入

得：t＝0.333mm；F＝1674.15N／mm2。其中：F为面载荷；Fn为齿轮法向压力；ρ1，ρ2为两齿轮曲率半径；t为接触宽度。

利用PROE建立齿轮的参数化模型，无缝导入ANSYS软件，计算得到啮合齿轮的接触区域，然后通过定义材料属性，对模型进行网格划分，接触模型如图2所示。

图2 接触模型图

对于齿轮接触强度的计算是在静态分析的基础上，不考虑齿轮的制造误差和安装误差，施加约束是定义齿轮轴孔内径上的点x，y，z方向以及u，v，w位移约束均为零，假设齿轮传动为面接触，施加面载荷并求解得到齿轮的等效应力云图（图3）。

图3 齿轮接触应力云图

从图3可以看出，经有限元软件优化参数后计算得到的最大接触用力为991.5MPa，查表得到许用接触用力［σH］为1 666MPa，说明优化后的齿轮完全符合实际使用需求。

3 结束语

以水陆两用机耕船换轮减速箱的体积为最小目标函数，并且确定了m，z，φ为参数的设计变量，并根据受力情况为约束条件定义S＝bt边界条件，对齿轮副进行了优化，最后体积减少了21.29%，经有限元软件ANSYS检验后接触应力在许用范围内。

［1］ 张小芹，王海芳，孙 磊，等.基于神经网络及遗传算法的齿轮优化设计软件［J］.机械设计及制造，2010（10）：32－34

［2］ 王帅宝，莫云辉.基于改进蚁群算法的斜齿轮传动动态优化研究.［J］机械制造.2009（07）：27－28

［3］ 王占奎，薛春善.基于遗传粒子群算法的圆柱齿轮优化设计与实现［J］.河南科技学院学报自然科学版，2008（01）：85－87.

［4］ 毛志伟.变速箱齿轮噪音分析与优化［D］.南昌：南昌大学，2012.

［5］ 蔡 新，李洪煊，武颖利，等.工程结构优化设计研究进展［J］.河海大学学报自然科学版，2011（03）：36－43.

［6］ 董立立，赵益萍，梁林泉，等.机械优化设计理论方法研究综述［J］.机床与液压，2010（15）：120－125.

［7］ 李万祥.工程优化设计与 MATLAB实现［M］.北京：清华大学出版社.2009：211－219.

［8］ 韩服善，欧阳小安.避免圆柱齿轮干涉及根切的最小齿数研究［J］.机械设计与制造，2009（07）：147－149.

［9］ 刘斌彬.ANSYS有限元齿轮接触及弯曲应力研究［J］.机电技术，2009（03）：74－75.