模糊理论在数控铣床加工中的应用研究

周宝同，林 岗

（河海大学 机电工程学院，江苏 常州 213022）

数控铣床是加工制造过程的重要制造装备。近年来，虽然数控铣床的发展取得了长足的进步，但随着生产力的发展，传统的数控铣床显露出了弊端。它是基于对零件工艺分析，编制数控程序，属于非实时控制加工，出于对加工母机，刀具保护等考量，加工参数选取的比较保守，不能充分发挥数控机床的性能，造成了很大程度上的资源浪费。因此，研究新的铣削过程控制方法，提高加工效率，具有较大的工程价值。

1 模糊控制系统设计

1.1 模糊控制的概述

模糊控制的概念是由美国加利福利亚大学教授L.A.Zadeh提出来的。模糊理论的引入，可将人的判断，长期累积的经验，思维过程用一套数学形式表达出来，从而使对复杂系统或无法建立精确数控模型的系统做出合乎实际的，符合人类思维方式的处理成为可能。较传统控制而言，数控铣床应用模糊控制具有较多优点。

1.2 模糊控制的系统框架

数控铣床的自适应模糊控制系统结构[1-2]，如图1所示。模糊控制器是实现自适应调节参数的核心部分，它输出一个速度给运动控制卡，运动控制卡根据速度调节脉冲输出给伺服电机，伺服电机通过放大作用，驱动伺服马达带动进给机构。同时测量伺服电机电流，转换成功率参数，与给定恒功率相比较，完成一个周期的循环控制作用。

图1 数控铣床自适应控制结构图Fig.1 Structure diagram of milline machine in self-adaptation control

1.3 模糊控制器的设计

一个完整的模糊控制器主要包括3个方面的内容：模糊量的精确化，将一个精确的输入转换成一个模糊集合；模糊控制算法的设计，编制模糊控制规则，实现恒功率控制；输出信息的模糊判决，将一个模糊的量精确化输入到控制器上。

1.3.1 输入量的模糊化

在控制系统中，模糊控制器的输入语言变量E和EC的量测值都是确定数，但模糊控制器的输入要求为模糊集合，因此需要将精确值模糊化[3]。在本论文中，选定伺服电机额定功率为400 W，误差e的基本论域为[-30，30]，误差变化率e论域为[-24，24]，控制量变化 u 的基本论域为[-36，36]，n 均取 6。

根据误差的实时测量值 e1，以及量化因子ke，由ni=ke×e1求取e1在基本论域[-30，30]上的量化等级，然后查找语言变量E的赋值表，找出在元素ni上与最大隶属度对应的语言值所决定的模糊集合。该模糊集合便代表确定数e1的模糊化。

1.3.2 模糊控制算法的设计

由模糊控制控制器误差基本论域为 [-30，30]，E的论域X={-6，-5， …，0， …+5，+6}， 得误差 e的量化因子 ke=6/30=0.2，为语言变量选取 7 个语言值：PB，PM，PS，0，NS，NM，NB。根据实际操作者的实践经验[5]，可建立语言变量E的赋值表，如表1所示。

表1 语言变量E的赋值表Tab.1 Language variable e assignment table

用同样的方法可建立语言变量EC和U的赋值表。基于操作者手动控制策略的总结，得出一组有49条模糊条件语句构成的模糊控制规则，将这些模糊条件语句加以归纳，可建立数控铣床恒功率系统控制规则的模糊控制状态表，如表2所示，表中有X号称为死区。

表2 模糊状态控制表Tab.2 Fuzzy control state table

模糊空控制状态表2包含的每一条模糊条件语句都决定一个模糊关系[6]，它们共有49个，事例计算如下：

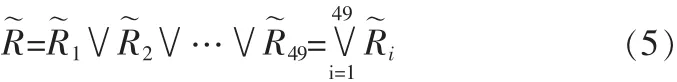
1.3.3 输出量的模糊判决

模糊控制器的输出是一个集合，但要是对伺服电机进行控制，就必须给出一个精确的量，那么有必要对该模糊集合进行解模糊计算。离线建立该解模糊查询表，把它存放到计算机的存储器上，编写一个查找查询表的子程序。在实际控制过程中，在一个采集周期内，将采集到的误差e（k）和计算得到的误差变化e（k）-e（k-1）分别乘以量化因子得到相应论域中的元素，到查询表中查询，即可得到所需的控制量uij，乘以比例因子ku，即为所需加到被控过程的实际控制量变化值。

2 仿真实验

为了验证该控制方法对数控系统的实用性，以数控系统上使用的某种伺服电为例，对当数控铣削加工情况发生变化时，伺服电机自我调节能力进行了仿真[6-7]。其数学模如图2所示。

模拟当铣削力变化为80N时，控制系统的相应曲线如图3所示。

从图中可以看出，控制响应曲线最大超调量约为2.5，响应时间约为0.5 s，稳态误差较小，基本可以满足控制要求。

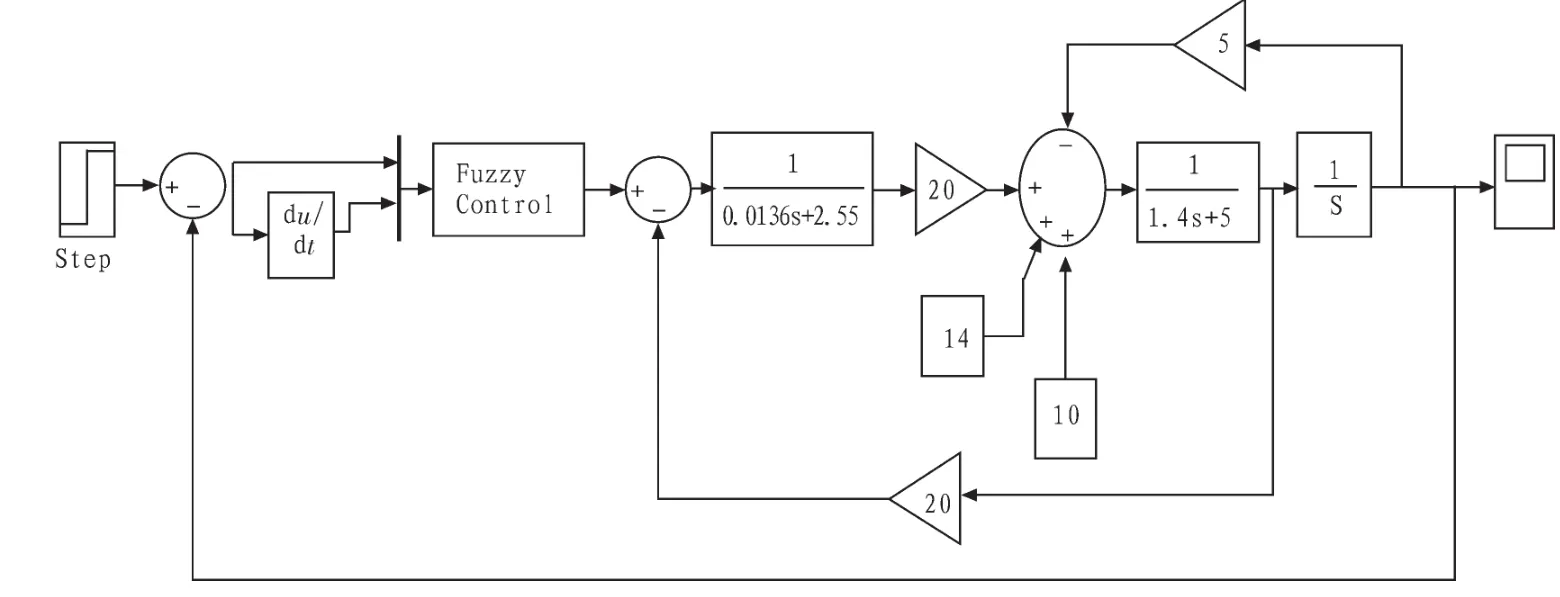
图2 伺服电机数学模型Fig.2 The mathematical model of servo motor

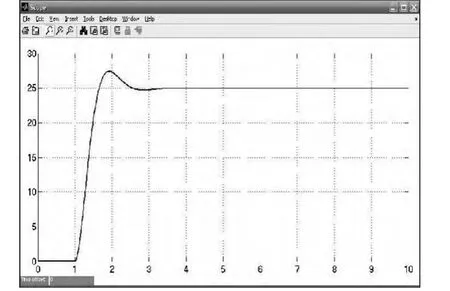
图3 伺服电机自适应控制响应曲线Fig.3 Response curve of servo motor

3 结束语

文中提出的将模糊控制[8]应用于数控铣床加工过程自适应控制，以恒功率为约束目标，能够有效提高加工效率和快速调整铣床加工趋向稳定状态，研究表明可以提高加工效率20%以上[1]，部分地区已开始推广使用，有广泛的应用前景。

[1]任永忠.数控加工智能控制系统的研制[D].西安：西安科技学院，2003.

[2]王德斌.运动控制系统及其在机床数控化改造中的应用关于研究[D].上海：上海交通大学，2007.

[3]许家民.基于传感器的加工过程只能控制技术研究[D].常州：河海大学，2007.

[4]章卫国.杨向忠 模糊控制理论与应用[M].西安：西北工业大学出版社，2000.

[5]黄卫华.方康玲 模糊控制系统及应用[M].北京：电子工业出版社，2012.

[6]王宏华.王时胜 现代控制理论[M].北京：电子工业出版社，2013.

[7]张国良，曾静，柯熙政，等.模糊控制及其MATLAB应用[M].西安：西安交通大学出版社，2012.

[8]林涛，刘仰魁，陈克斌.基于模糊控制的入口匝道智能控制方法[J].电子科技，2012（8）:100-103.LIN Tao，LIU Yang-kui，CHEN Ke-bin.Entrance ramp intelligent control method based on fuzzy control[J].Electronic Science and Technology，2012（8）:100-103.