基于频繁链表-存取树的Web用户浏览模式挖掘算法

邱奕飞，马 力

（西安邮电大学 计算机学院，陕西 西安 710061）

了解用户的访问行为，挖掘用户偏爱的浏览模式，对于改善网站的系统设计，进行合理的市场决策都具有十分重要的意义[1]。浏览模式，即某一个用户于浏览器频繁地对一系列地址的连续依次浏览所留下的轨迹。这种轨迹在很大程度上能够反映该用户本人对特定的“事物”、“活动”以及“人为对象”所产生的带有倾向性、选择性的态度、情绪和想法，即兴趣。进一步地，对用户浏览轨迹的长期观察，可以获得用户兴趣的变化。一方面，从而过滤出该用户固有的、长期的兴趣点。另一方面，从而跟踪用户兴趣的迁移轨迹，以研究、预判用户的兴趣迁移方向。

关联规则领域的最经典算法就是Apriori算法，是一种最有影响的挖掘布尔关联规则频繁项集的算法。其核心是基于两阶段频集思想的递推算法，但是该算法在实际应用时，存在着很多缺陷，比如需要多次扫描事务数据库，需要很大的I/O负载，而且可能产生庞大的候选集[2]。GSP（Generalized Sequential Patterns，广义序列模式）[3]算法是 Srikant和 Agrawal于1996年开发的一种序列模式挖掘算法。它是Apriori算法的原创性频繁项集挖掘算法的扩展。GSP采用多次扫描的候选产生-测试的方法生成序列模式。PNT（Preferred Navigation Tree，浏览偏爱树）[4]是一种用来存储用户浏览信息的树结构。相比用户会话期数据库，该结构占用较小的空间。但是这种结构的挖掘往往会遗留那些不是由根节点出发的 “散落”的偏爱路径，而无法全面地得到所有的偏爱浏览模式。

1 频繁链表—存取树的基本逻辑结构

频繁链表—存取树结构（Frequent Link and Access Tree，FLaAT）[5]，是wu等人提出的一种频繁链表结合存取树的结构。为了完备地找到所有偏爱路径，FLaAT采用类似PNT的树结构，外加一个频繁链表。而频繁链表配合next链（见下文）很好地捕捉了PNT所遗漏的偏爱模式。整个FLaAT总体上由一棵存取树和一张频繁链表组成。本文将用于存储用户访问路径的FLaAT结构进行了变形，变形后的用户兴趣FLaAT结构如图1所示。

图1 用户兴趣FLaAT结构图Fig.1 User interest FLaAT structure

1.1 存取树的基本结构

存取树事实上一种基于链表的结构，换言之，整棵树相当于一个根节点本身。节点用于表示用户浏览轨迹中所包含（途经）的兴趣点。每个节点包含6个属性（此处仅介绍逻辑结构）：interest、support、preference、child、younger以及 next。 其中：Interest即“兴趣”，是指该节点所表示的兴趣本身，即预定义的主题分类中的一个。support即“支持度”，是指截至当前所统计到的，经过该节点的浏览轨迹的总数。child即“孩子”，指向该节点的孩子节点。younger即“兄弟”，指向该节点的下一个兄弟节点。

事实上，在存取树中，一个节点的“孩子们”是以：“孩子”、“孩子的兄弟”、“孩子的兄弟的兄弟”、“孩子的兄弟的兄弟的兄弟”......（下文称“兄弟链”）的形式存在的。

preference意为“偏爱度”，定义如下：

定义2.0：平均访问度f：设x为某节点。若x没有孩子，则x.f不存在。若x有孩子y，则统计y的所有兄弟节点个数n（即沿y的兄弟链检索直到某节点无兄弟节点为止）。那么，x的平均访问度

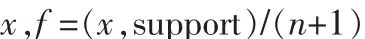
定义2.1：偏爱度[6]p：设x为某非根节点。z为x的“父亲”（即x是z的孩子，或者x在z的孩子的兄弟链上），那么，x的偏爱度

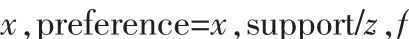
next指向下一个 “同类”节点 （即与该节点拥有相同interest之节点），具体意义将在1.2节中指出。

1.2 频繁链表的基本结构

频繁链表事实上是一张向量表，其中每一个元素被称为一个“组”（team）。组负责监管整棵树中某一个兴趣分类。每一个组包含3个属性 （此处仅介绍逻辑结构）：interest、count以及first。其中：interest即“兴趣”，是指该组所监管的兴趣分类。count即“计数”，是指该兴趣在全局被访问的总次数。first即“第一个”，是指从频繁链表出发的，树中第一个（未必是时间上）包含该兴趣的节点。由于用户浏览轨迹的多变性，同一个兴趣点，可能分布在多条路径上，即存在多个代表相同兴趣的节点。first指向第一个该兴趣节点，而被指向节点的next值为全局中下一个同兴趣节点，以此类推。换言之，全局隶属于同一个兴趣分类的不同节点（至少一个），由频繁链表中监管该兴趣的组中的first项发起，这些节点中的next值参与，共同搭建了一条形如“first-next-next...”的链表（下文称“next链”）。这样，通过频繁链表的每一个组，都可以便利地检索到全局所有该兴趣的节点，大大降低了挖掘难度。next链的整体结构如图2所示。

2 FLaAT的构建与更新算法

FLaAT即一张表和一棵树。FLaAT的主体数据结构是链表，而链表的特性使得整体结构面临增、改操作时所付出的代价极小。因此，在已经处理完一批数据（即频繁链表与树结构已经完全建立）的情况下，FLaAT对后续新数据极其欢迎，这也十分符合FLaAT被用于长期增量式跟踪挖掘工作的任务特性。

图2 兴趣“A”的next链Fig.2 The next chain of interest“A”

对于一个增量式的数据结构，如果更新一次的过程就是“n+1”的过程，那么创建的过程就是 “0+1”的过程。因此FLaAT的更新算法与创建算法本质上是统一的。

表1 FLaAT的更新算法Tab.1 Update algorithm of FLaAT

所有已经获得的用户浏览轨迹被依次添加进FLaAT中，同时，新获取的轨迹也及时地更新之，使得整个FLaAT完整的记录用户的浏览行为。然而要得到用户的偏爱浏览模式集，还需要对FLaAT进行挖掘。

3 FLaAT的挖掘算法

对FLaAT的挖掘，主要目的就是从整棵存取树中找出用户相对比较频繁地“走过”的路径。事实上，我们需要一对阈值，来定义何为频繁、何为偏爱。这对阈值正是support和preference，在FLaAT中，存取树主要负责保存所有的浏览路径的信息，而频繁链表则主要用于挖掘。整体的挖掘工作就是从频繁链表出发的。频繁链表从全局的角度，按兴趣不同进行分类，横向地、完整地跟踪着所有节点。设想我们已经获取了7条浏览轨迹如下表：

表2 已经得到的某网络用户的7条浏览轨迹Tab.2 A web user’s seven browsing tracks

表中的字母分别代表一个兴趣分类。我们利用上述信息建立一个FLaAT如下图：

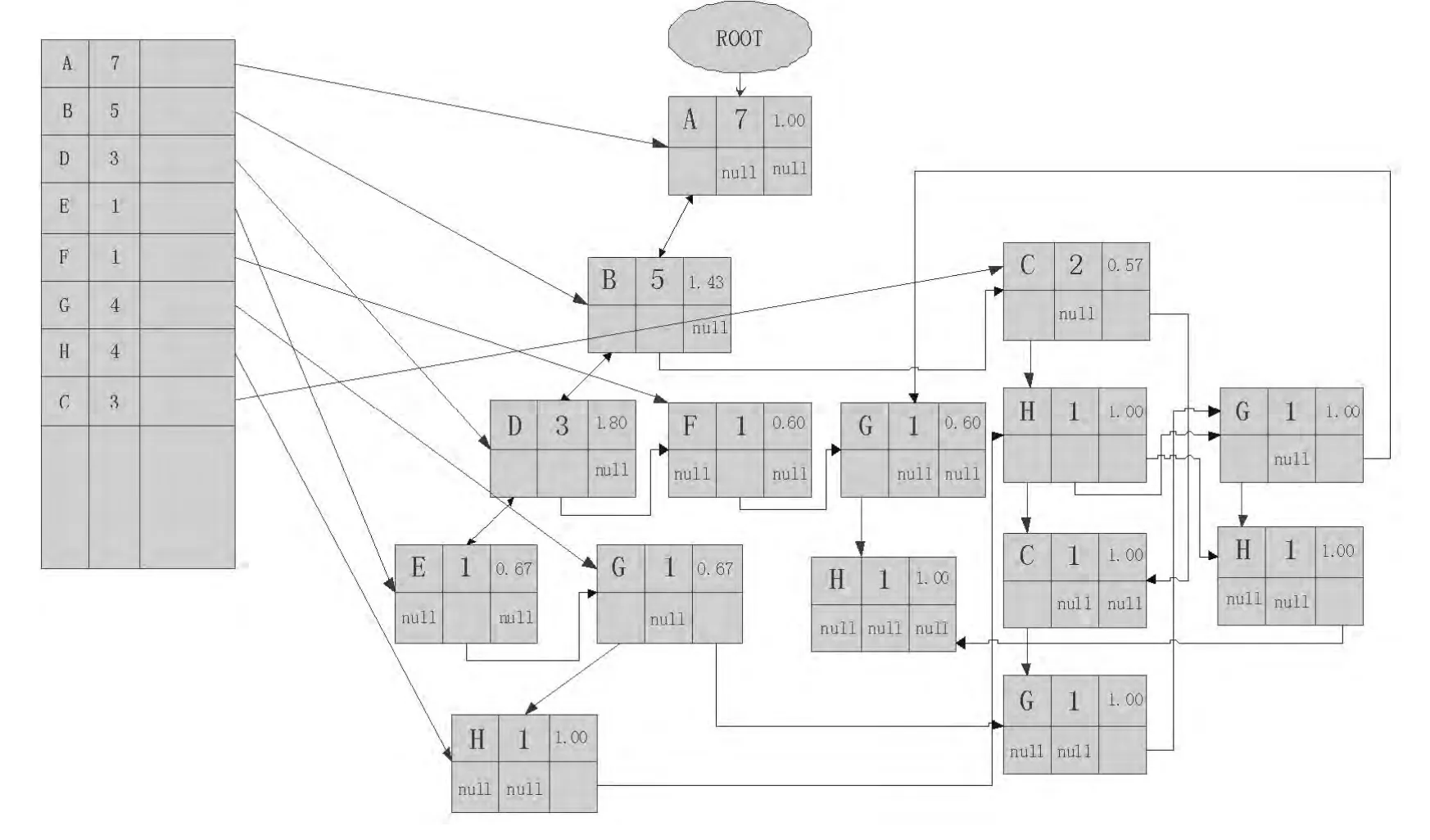
图3 建立完整的FLaAT结构Fig.3 A complete FLaAT Structure established

我们不妨令 support阈值为 2，preference阈值为 0.5，开始挖掘我们从频繁链表出发依次遍历每一条next链，即每一个兴趣分类（频繁链表中count值达不到support阈值的分类在树中不可能存在有价值的待挖掘浏览模式，故直接跳过，即在例子中，排除分类E、F）。只要简单地检测每一条分支便可得到符合要求的路径：ABD、AC。但事实上，这样做不完备。如果单纯的比较每一个节点的阈值，往往会遗漏掉如GH这样出现次数多但不集中的路径。因此我们对于每一条next链都先要做一件事：把整个next链上的所有节点聚合到first所指向的第一个节点上。具体地，我们先将next链上所有的节点为根，逆向翻译成原始兴趣序列，然后调用FLaAT更新算法，将这些序列逐条添加到first所指向的第一个节点上，形成一棵以该节点为根的小型存取树（如图4）。

完成了以上工作之后，再检测每一条分支便可得到符合要求的路径。将以上工作依次执行于所有兴趣分类上，所得解为完备解。该挖掘算法具体如下：

图4 同类合并算法Fig.4 Similar merging algorithm

该算法的时间复杂度与序列中的元素个数成线性比例关系，在这一点上，与GSP算法持平。

表3 FLaAT频繁模式挖掘算法Tab.3 Frequent pattern mining algorithms of FLaAT

4 实验分析

本文的实验数据集是使用Winpcap在局域网中捕获用户一个月以来所发送的数据包，然后提取出其中有效的URL，接着依据这些URL使用网页爬虫程序取得的用户浏览网页。通过对捕捉到的浏览页面进行URL分析汇总后得到712个浏览页面，分析后取了其中的302个有用页面进行挖掘，分别编号为1，2，…，302。实验条件如下：

处 理 器 ：Intel Core i7-3612QM； 内 存 ：8.00GB；OS：windows7；平台：Java version1.7。

将基于FLaAT结构的序列挖掘与传统的序列挖掘模式算法GSP算法进行比较，在相同规模的数据集中分别采用两种方法进行序列挖掘，然后不断扩大数据集规模，多次进行实验，分别比较两种挖掘算法的准确性和耗时。比较结果如图5，图6所示。

图5为两种算法挖掘结果准确性比较图。在比较时，将两种算法的支持度阈值同时设为4，由图可以看出两种算法在挖掘时的准确性没有很大的差距，由于GSP算法最终挖掘的序列中只保留最长模式的序列，所以有一些频繁的子序列就会被GSP算法丢弃，随着数据规模的增大，GSP算法的挖掘结果准确性下降幅度增大。

图5 准确性比较Fig.5 Comparison of the accuracy

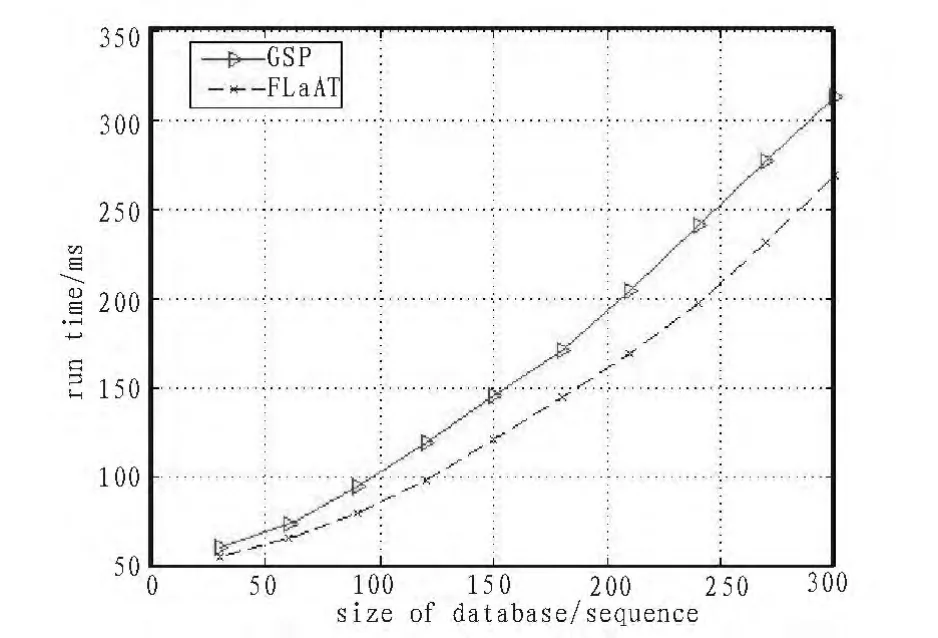
图6 耗时比较Fig.6 Comparison of time-consuming

图6 是两种算法的耗时比较图。由图中可以看出，由于GSP算法在挖掘过程中需要不断的对数据库重复扫描，所以当数据集规模不断增大时，算法执行需要的时间增长的很快，而基于FLaAT结构的挖掘，每当数据集规模扩大时，只需要对FLaAT进行更新即可，随着数据集规模的扩大，执行时间的增长明显较为缓慢。

5 结 论

文中将频繁链表-存取树结构应用于web浏览模式的挖掘领域，实现了更新与挖掘算法，并对该算法的效率和准确度等性能和GSP算法进行了比较研究。

任何时刻，我们通过挖掘所得的偏爱浏览模式集，只能够反映用户截至当前的兴趣分布状况。后续得到的新的浏览轨迹包含着用户兴趣的迁移状况。为此，以捕获用户浏览轨迹的定期性和长期性为前提，我们可以定义一个“有效时段”，即在过去的N天内的浏览轨迹为有效轨迹。这样，FLaAT在不断更新的同时，须删除N天之前的轨迹（参照更新算法），然后进行挖掘，并更新用户偏爱浏览模式集。如此，能够常驻偏爱集的浏览模式即该用户的长期固有兴趣；而不断变化的部分可作为参考以研究用户兴趣变化方向。

[1]LI Yu-xia，LI Hong-yu.Data Mining Algorithm of Browsing Pattern Based on Web Log.Knowledge Acquisition and Modeling， 2011 Fourth International Symposium [C].2011.88:307-311.

[2]刘宏强.Apriori关联规则挖掘算法分析与改进[J].中国石油大学胜利学院学报，2009，23（7）:17-19 LIU Hong-qiang.Analysis and improvement of apriori association rule mining algorithm[J].Journal of Shengli College China University of Petroleum，2009，23（7）:17-19.

[3]陈卓，杨炳儒.序列模式挖掘综述[J].计算机应用研究，2008，25（7）:1961-1976.CHEN Zhuo，YANG Bin-ru.Summary of sequential pattern mining[J].Application Research of Computers，2008，25（7）:1961-1976.

[4]Xing D，Shen J.Efficient Data Mining for Web Navigation Pattern[J].Information and Software Technology，2004（46）:55-63.

[5]吴瑞，张秀玲.基于FLAAT的加权偏爱模式的挖掘算法[J].计算机工程与应用，2005，41（19）:182-184.WU Rui，ZHANG Xiu-ling.Mining algorithm based on a weighted preference patterns FLAAT[J].Computer Engineering and Applications，2005，41（19）:182-184.

[6]Attwood T K，Parry-S D J mith.生物信息学概论[M].罗静初等译.北京:北京大学出版社.2002.