基于划分的聚类算法研究综述

贾瑷玮

（陕西师范大学 计算机科学学院，陕西 西安 710062）

把单个的数据对象的集合划分为相类似的样本组成的多个簇或多个类的过程，这就叫聚类[1]。 在无监督的情况下，具有独立的学习能力，这就是聚类。将数据空间中的所有数据点分别划分到不同的类中，相近距离的划分到相同类，较远距离的划分到不同类，这就是聚类的目的.聚类分析常作为一种数据的预处理过程被用于许多应用当中，它是更深一步分析数据、处理数据的基础。人们通过聚类分析这一最有效的手段来认识事物、探索事物之间的内在联系，而且，关联规则等分析算法的预处理步骤也可以用它。现在，在气象分析中，在图像处理时，在模式识别领域，在食品检验过程中，都有用到它。随着现代科技水平的不断提高、网络的迅猛发展、计算机技术的不断改革和创新，大批量的数据不断涌现。怎样从这些数据中提取有意义的信息成为人们关注的问题。这对聚类分析技术来说无疑是个巨大的挑战。只有具有处理高维的数据的能力的聚类算法才能解决该问题.研究者们开始设计各种聚类算法，于是，基于划分的聚类算法便应运而生，而且，取得了很好的效果。

1 聚类概述

1.1 定义

聚类的定义为:在已知的数据的集合中，寻找数据点集的同类的集合.其中，每一个数据集合为一个类，还确定了一个区域，区域中的对象的密度高于其他区域中的对象的密度.

聚类的实质就是“把数据集合中的所有数据分成许多的类簇，其中必有一个类簇内的实体它们都是相似的，而其它不同类簇的实体它们是不相似的；一个类簇是被测试空间中的点的会聚，而且，同一个类簇的任意两个点之间的距离小于不同的类簇的任意两个点之间的距离；一个包含的密度相对较高的点集的多维空间中的连通区域可以被描述为一个类簇，这时，它们可以借助包含的密度相对较低的点集的区域与其他的区域分离开来。”

1.2 聚类算法的种类

截止目前，经典的聚类方法有基于划分的方法，也有基于层次的方法，更有基于密度的方法，还有基于网格的方法及基于模型的方法。

1.2.1 划分方法（partitioning methods）

给定一个数据集D，其包含有n个数据对象，用一个划分方法来构建数据的k个划分，每一个划分表示一个类，且k≤n。即它将数据对象划分为个簇，并满足以下两点要求:1）每一个组至少包含一个数据对象；2）每一个数据对象必须属于某一个组.假定要构建的划分其数目为k，划分方法就是:首先，先创建一个初始的划分，然后，再采用一种迭代的重定位的技术，通过将数据对象在划分间来回的移动来改进划分.一个好划分的准则为:同一类中的数据对象之间要尽可能的“接近”，而不同的类中的数据对象之间要尽可能的“远离”。

1.2.2 层次方法（hierarchical methods）

对给定的数据对象的集合进行层次的分解就是层次的方法.依据层次分解的形成过程，该方法可分为凝聚的层次聚类和分裂的层次聚类两类.自底向上进行的层次分解为凝聚的（agglomerative）层次聚类；自顶向下进行的层次分解为分裂的（divisive）层次聚类.分裂的层次聚类先把全体对象放在一个类中，再将其渐渐地划分为越来越小的类，依此进行，一直到每一个对象能够自成一类.而凝聚的层次聚类则是先将每一个对象作为一个类，再将这些类逐渐地合并起来形成相对较大的类，依此进行，一直到所有的对象都在同一个类中方结束。

1.2.3 密度的方法（density-based methods）

大多数的聚类算法都是用距离来描述数据间的相似性性质的，这些方法只能发现球状的类，而在其他形状的类上，这些算法都无计可施.鉴于此，就只能用密度（密度实际就是对象或数据点的数目）将其的相似性予以取代，该方法就是基于密度的聚类算法。密度的方法的思想：一旦“领域”的密度超过某一个阈值，就将给定的簇继续的增长.该算法还能有效的去除噪声。

1.2.4 网格的方法（grid-based methods）

先把对象空间量化成有限数目的单元，将其形成一个网格空间，再对该空间进行聚类，这就是网格的方法.其主要优点为处理速度快，因为它的处理速度只与量化空间中的每一维的单元数目相关，而与数据对象的数目无关.

1.2.5 模型的方法（model-based methods）

基于模型的方法就是先给每一个聚类假定一个模型，再去寻找能较好的满足该模型的数据的集合。此模型也许是数据点在空间中的密度分布的函数，也许是其它.其潜在的假定为:一系列概率的分布决定该目标数据的集合.统计方案、神经网络方案通常是其研究的两种方向。

2 基于划分的聚类算法

给定一个数据集D，其包含有n个数据对象，用一个划分方法来构建数据的k个划分，每一个划分表示一个类，且k≤n。根据D的属性，使得同一类中的数据对象之间尽可能的“接近”，而不同的类中的数据对象之间尽可能的“远离”。

2.1 K均值聚类算法

2.1.1 K均值聚类算法基本原理

随机选k个点作为初始的聚类的中心点，根据每个样本到聚类的中心之间的距离，把样本归类到相距它距离最近的聚类中心代表的类中，再计算样本均值.如若相邻的两个聚类中心无变化，调整立即结束，如若不然，该过程不端重复进行。其特点是:在每次迭代的时候，均要检查每一个样本分类，看该分类是否正确，不正确的话，就要在全部的样本中进行调整，调整好后，对聚类的中心进行修改，再进行下一次迭代；如若分类正确，聚类的中心就不再调整了，标准测度函数也就收敛了，算法也就结束了。

2.1.2 K均值聚类算法步骤

输入项为:簇的数目k及包含有n个对象的数据的集合。

输出项为:k个簇。

具体的方法:

1）在数据的对象的集合中，任选k个对象作为初始的簇的中心；

2）依据簇中的对象的平均值，为每一个对象重新予以最相似的簇；

3）更新簇的平均值 （即计算每一个簇中的对象的平均值）；

4）重复 2）3）两个步骤；

5）一直到不再发生变化为止。

2.1.3 K均值聚类算法性能分析

优点:该算法的运算速度非常快，而且其结构也很简洁；其类簇之间的区别也很明显；最重要的是其时间复杂度为O（nkt），所以，在处理大型数据集时，它具有可伸缩性和高效性.其中，n是样本的数目，k是类簇的数目，t是迭代的次数，通常 k≤n 且 t≤n。

缺点:该算法需要事先给定簇类的数目k；它不适合非凸形状的簇，也不适合存在大小差别很大的簇的数据的集合；其对数据集合内的噪声和离群点的敏感较高，因为此类数据也许会对均值造成一定的影响；因为其对初始中心的选择的依赖性较强，所以，产生局部的最优解发生的概率非常大。

2.2 K中心点聚类算法

2.2.1 K中心点聚类算法的基本原理

首先，针对每个类，先为其随机的选择一个实际样本，将其作为初始的中心点，而数据集内剩余的其他样本则依据其与中心点样本的相似度，将其分配到最相似的中心点所在的簇类内，然后，再选择新的中心点对象将原来的中心点对象替换掉，以此达到提高聚类质量（聚类质量是由数据集内的各个样本与所属簇的中心点间的平均相异度来度量的。）的目的，如此反复的选择，一直到聚类质量不再提高为止.用接近聚类中心的一个数据对象来表示K中心点聚类算法的簇，而在K均值聚类算法中，用该簇中数据对象的平均值来表示每个簇。

2.2.2 最早提出的K中心点聚类算法

PAM（Partioning around Medoid）是最早提出的K中心点聚类算法.其原理为:先为每个类任选一个代表对象，而剩下的数据对象则根据其与代表对象的距离远近而相应的加入到最近的类中，再尝试着用非代表数据对象将代表数据对象替换掉，如此反复尝试，直至收敛。

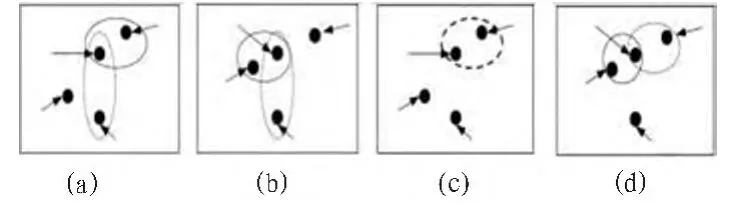
图1 PAM算法过程示意图Fig.1 PAM algorithm process diagram

假定Orandom表示非聚类代表对象，Oj表示聚类代表对象，为确定任一Orandom是否可替换当前Oj，需根据以下4种情况来分别对各非聚类代表对象P进行检查。

1）若P当前属于Oj所代表的聚类，且若用Orandom替换Oj，将Orandom作为新聚类的代表，而P则更接近于其他Oi，其中（i≠j），那么则将P归类到Oi所代表的聚类当中。

2）若P当前属于Oj所代表的聚类，且若用Orandom替换Oj，将Orandom作为新聚类的代表，而 P则更接近 Orandom，那么则将P归类到Orandom所代表的聚类当中.

3）若 P当前属于 Oi所代表的聚类，其中（i≠j）， 且若用Orandom替换Oj，将Orandom作为新聚类的代表，而P仍然最接近Oi，那么P的归类将不发生任何变化.

4）若 P当前属于 Oi所代表的聚类，其中（i≠j）， 且若用Orandom替换Oj，将Orandom作为新聚类的代表，而P最更接近Orandom，那么则将P归类到Orandom所代表的聚类当中.

构成成本函数的方差会随着每次对对象进行重新归类的时候而发生变化，于是，成本函数可以计算出聚类代表替换前和替换后的方差的变化.成本函数的输出可以通过替换掉不合适的代表而使距离方差发生变化的累计而构成。整个输出成本为负值时，用Orandom替换Oj，以达到减少实际方差E的目的。整个输出成本为正值是，可认为当前Oj可接受，本次循环无需再做变动。

2.2.3 新兴进化的K中心点聚类算法

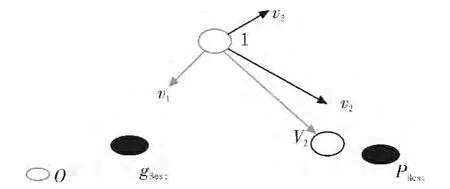
图2 粒子空间变化示意图Fig.2 Particles schematic space change

1995年，James Kennedy等人受到鸟群觅食行为的启发，提出了一种模拟社会行为的进化的计算方法PSO（Particle Swarm Optimization）.该算法先初始化为一群随机的粒子，通过迭代的方法，找到最优的解。每次迭代，粒子都会通过跟踪两个极值以此来更新自己:一个极值为粒子本身找到的最优解，该解被称为个体极值，而另一极值则是整个种群目前所找到的最优的解，该极值被称为全局极值.粒子在空间中的速度变化如图2所示。

粒子将按照以下公式更新自己的速度和位置，以此来寻找到上述两个最优值:

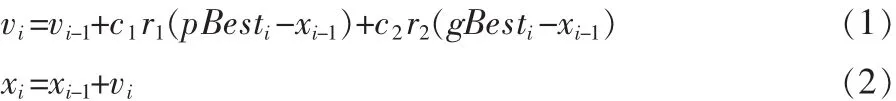
上述（1）、（2）式中，c1和 c2是加速常数，通常情况下，c1和 c2在[0，4]之间选值，一般情况，取 c1=c2=2；r1和 r2则是[0，1]之间的两个随机的数。每一个粒子的位置、速度都会以随机的方式来初始化，以后，粒子的速度将会朝着全局最优及个体最优的方向而逐步靠近。

2.2.4 K中心点聚类算法性能分析

K中心点聚类算法有很强的鲁棒性，因为它用簇内真实样本作为簇中心，这样可以降低噪音及离群点对聚类结果做产生的影响.但缺点是，它不适合于大型的数据集，由其初始的中心是随机选的，仍会存在局部最优解，且时间复杂度为O（k（n-k）2），时间复杂度较大。 由此看来，只要确定恰当的聚类数目k值及初始的聚类中心点，才能加快聚类过程的收敛的速度，以提高聚类的效率。

2.3 基于划分的聚类算法研究现状

近几年来，人们对于基于划分的聚类挖掘技术的研究，研究最多的、发展较快的也就是对K均值聚类算法的改进.Mac Queen在1967年提出了K均值聚类算法的概念，但该算法不能发现非凸面，而且，对噪声数据的敏感过强.于是，学者们又对其进行改进，在1990年的时候，Rousseeuw等人提出了PAM和CLARA（Clustering Large Applications）算法。国内外研究者们大都把目光集中在聚类中心的初始化和聚类数目k值的确定问题上，但是，聚类中心的初始化和聚类数目k值并没有普遍适用的解决的办法[2]。

2.3.1 关于聚类中心初始化的改进

1）Forgy最早提出任选k个数据对象，将其作为初始聚类的中心（也有人把随机的选择初始聚类中心的方法称之为FA（ForgyApproach））；2）根据最大距离和最小距离的聚类方法来寻找聚类的中心，以此来确定初始的聚类中心，如BK Mishra等人于2012年提出的Far Efficient K-Means聚类算法；3）直观的用将预理数据集内的混合样本分成k类的方法，计算出各个类的均值，将其作为初始的聚类中心；4）最具有代表性的基于数据采样的方法就是Bradley等人提出的RA算法；5）通过“密度法”选择数据样本，将该样本作为初始的聚类中心.2008年的时候，Park等人对密度提出了一种全新的定义[3]，计算的数据集中了所有数据对象的密度，且选密度最小的k个数据对象，将它们作为初始的聚类中心；6）用全局的思想来初始化聚类中心。Likas等学者发明了全局K均值聚类的算法，该算法是根据递增的思想提出的，把k个簇的聚类问题转变成一系列的子聚类的问题，先从一个簇的聚类问题开始，每增加一个簇，就用迭代的方法求出k个簇的聚类问题.后来，许多学者对该算法进行研究，并在它的基础上做了一些改进；7）多次对初始值进行选择和聚类，将最优的聚类结果找出。

2.3.2 关于聚类数目k值的确定

G.W.Milligan[4]在1985年时就最先提出了通过测试的方法来得到最佳的聚类数目k值的思想.其思想就是:对一定范围内的所有的聚类数目进行测试，观察它们的收敛速度，得出最优的k值。紧接着，Xu使用一种被称之为次胜者受罚的竞争的学习规则来自动的决定类的适当数目。其思想就是:对每个输入，竞争获胜的单元的权值将被修正以适应输入值，次胜的单元将采用惩罚的方式使其远离输入值。后期，S.Ray等人研究出了一种新的确定最优k值的方法，它是基于Milligan而提出的.其思想为:主要考虑类内和类间的距离，认定类内足够紧凑且类间足够分离时，此时的k值是最优的.他们还引入了v（validity）值，v值表示类内的距离与类间的距离的比值，在迭代时计算出k值最小的时候，其对应的k值，此k值就是最优的k值。根据方差分析的理论，孙才志等人提出了应用混合F统计量来确定最佳的分类数，不仅如此，他还应用模糊划分嫡来验证最佳的分类数正确与否。

2.4 其他对于K-均值聚类算法的改进

针对K-均值聚类算法极易陷入局部最优解的问题，刘伟民等研究人员将K-均值算法和模拟退火算法进行结合，得出一种新的算法，以模拟退火算法的全局寻找最优解的能力来解决此问题。为防止算法陷入到局部极小值，加快收敛的速度，刘韬将一种免疫的计算方法与K-均值聚类算法结合起来，为每一个抗体的亲和度及浓度进行了重新定义，对繁殖率的计算及复制和变异的方法进行了重新的设计。面对K-均值聚类算法对其它形状的类簇不敏感或不识别的问题，于是，易云飞又一次对K-均值聚类算法进行了改进，它用复合形粒子群的算法对聚类的初始中心点进行选取，再通过执行K-均值聚类算法，最终得到聚类的结果。郑超等人对粗糙集进行了改进，将其与K-均值聚类算法结合起来，提出了一种全新的算法.该算法对每个样本点所在的区域的密度值进行了考虑，在求均值点过程中加入了权重的计算，规避了噪音点数据对聚类结果产生的影响。

3 基于划分的聚类分析技术具体应用

多数学者对基于划分的聚类算法的研究大都在对算法的改进方面，而将算法应用于具体领域的很少。现在该算法的应用方向集中在图像的分割与识别、文本的聚类、基于聚类的入侵检测、空间的约束聚类等方面.Cui Xiao-hui[5]将PSO、K-means和混合PSO算法应用于四种不同的文本文件，并对其数据集进行聚类，聚类后，经比较分析，混合PSO算法得到的聚簇结果非常紧致，而且用时非常短。文献[6]中，学者们把PSO与K-means方法结合起来，新发明了一种PSO-KM的聚类算法，并将该算法应用于无监督的异常的入侵检测当中.其优点是与输入样本和初始的权值的选择无直接的联系，全局搜索能力比K-means强.将该算法在KDD Cup 1999数据集上做实验，结果显示:误报率2.8%时，检测率则为86%；此方法对Probe、Dos、U2R攻击类型的检测最为有效，正确度可达到 78%（U2R）到 94%（Dos）。X光图像中的鱼骨检测技术就是用基于质心划分的PSO聚类做的[7]。面对X光图像的灰度值分布的问题，是用高斯分布的工具与形态学的方法相结合，结合后将其应用于图像的预处理，以此来消减图像数据的规模，从而得到一个有效的区域。PSO聚类方法的作用则是将有效的区域分割成为不同的簇。与传统的图像分割技术Mean Shift比较，改良后的方法更为有效。

4 结束语

本文在查阅大量文献、资料、书籍的基础上，对基于划分的聚类算法进行了系统的学习和总结，主要对聚类的定义及聚类算法的种类进行了介绍，并对K均值聚类算法和K中心点聚类算法的基本原理进行了详细阐述，还对它们的性能进行了分析，梳理了基于划分的聚类算法的研究现状，最后，对其应用做了简要介绍.经过归纳与总结，基于划分的聚类算法主要有以下几方面研究方向:1）如何解决基于划分的聚类算法所不能解决的凸型聚类以外的子样集合问题；2）怎样选择值，使基于划分的聚类算法得以优化，性能更佳；3）如何选取初始的中心点，更大程度的增强基于划分的聚类算法的聚类效果；4）怎样对算法做出改进，使其能从各种聚类的结果中，筛选出或确定出最佳的聚类的分布.

[1]HAN Jia-wei，MICHELINE K.Data mining:concepts and techniques[M].San Francisco:Morgan Kaufmann Pubishers，2001.

[2]Duda R O，Hart P E．Pattem Classification and scene Analysis[M].New York:John Wiley and Sons，1973.

[3]Park H S，Jun C H.A simple and fast algorithm for K-medoids clustering[J].Expert Systems with Applications，2009，36（2）:3336-3341.

[4]Milligan G W，Cooper M C.Methodology Review:Clustering Methods[J].Applied Psychological Measurement，1987，11（4）:329-354.

[5]CUI Xiao-hui，POTOK T E.Document clustering analysis based on hybrid PSO+K-means algorithm [J].Journal of Computer Sciences:Special Issue，2006（4）:27-33.

[6]XIAO Li-zhong，SHAO Zhi-qing，LIU Gang.K-means algotithm based on particle swarm optimization algorithm for anomaly intrusion detection [C]//Proc of the 6th World Congress on Intelligent Control and Automation，2006:5854-5858.

[7]HAN Yan-fang，SHI Peng-fei.An efficient approach for fish bone detection based on image preprocessing and particle swarm clustering [C]//Advanced Intelligent Computing Theories and Applications，with Aspects of Contemporary Intelligent Computing Techniques.Berlin:Springer，2007:940-948.

[8]CUI Xiao-hui，POTOK T E.Document clustering analysis based on hybrid PSO+K-means algorithm [J].Journal of Computer Sciences:Special Issue，2006（4）:27-33.

[9]Huang Z.Extensions to the k-means algorithm for clustering large data sets with categorical values[J].Data Mining and Knowledge Discovery，1998：283-304.