AUV同时定位与跟踪算法研究

王 闯，卢 健，黄 杰

（西安工程大学 电子信息学院，陕西 西安710048）

0 引 言

与多合作自治水下航行器（简称AUV）间的协同导航［1－7］和高自定位精度AUV与非合作体间的目标跟踪［8－13］都不同，低自定位精度AUV与非合作体间的同时定位与跟踪（简称SLAT）要求AUV在运动过程中同时完成自身的准确定位和获取较高质量的非合作运动目标体的航迹信息.相比于协同导航与目标跟踪，SLAT的复杂之处在于SLAT的探测端位姿和被探测端位置都有很大的不确定性.携带低精度航位推算系统的AUV具有较高的推算误差，并且误差随时间的累积会使推算航迹严重脱离实际航迹.当其跟踪目标时，声纳系统探测到的与目标的相对距离、方位角也具有很大误差，AUV的航位推算系统、声纳探测信息的不确定性导致AUV自身的状态估计和被跟踪目标的状态估计同时具有不确定性.事实上，AUV的状态估计和目标的状态估计两者间相互依赖且相互影响.AUV要得到好的自身定位，必须有好的目标状态估计；要得到好的跟踪目标航迹，必须有好的自身定位.也就是说自身定位和目标状态估计要同时进行，而且估计结果都要保持一定的精度.

对于本文提出的SLAT问题，AUV与静态周边环境间的同时定位与制图（简称SLAM）［14－19］提供了一种解决此类两端状态都不确定问题的思路.SLAM可表述为：AUV在未知环境中从一个未知位姿出发，在航行过程中根据传感器观测和航位推算估计进行自身的定位，同时创建环境地图.SLAM方法中的基于EKF的随机地图创建法，是将AUV的位姿向量和环境特征向量组织在一个高维状态向量中，并引入能综合反应运动体与环境信息不确定性的系统协方差矩阵；而另外的一种在实际中广为应用的精度更高的FastSLAM算法，是基于Rao-Blackwellised粒子滤波器，利用粒子滤波器估计移动机器人的路径，并用每一个粒子所关联的若干个EKF分别估计环境特征的位置，很好地解决了在高维状态空间中进行采样时，粒子滤波效率低的问题.

仿照SLAM方法，本文提出了两种同时定位与跟踪（SLAT）的方法.SLAT分别利用EKF-SLAM和FastSLAM结构框架，并将其广义状态向量结构中的静态环境特征由运动目标的运动状态替代，为配备低精度航位推算系统的AUV使用自身携带的声纳传感器，结合滤波器稳定地跟踪非合作目标，并同时利用量测和对目标状态的估计值完成对自身航位推算误差修正的准确自定位过程.

1 模型基础

1.1 AUV的航位推算模型

为阐述方便，设只有1个AUV跟踪1个非合作目标M.进行跟踪的AUV在二维平面中的航位推算系统模型可表述为

其中 T（A），，为AUV的采样周期以及k时刻的本体传感器所得的运动速度和偏航角量测.其中：

1.2 目标运动的跟踪模型

虽然目标几乎从来不是一个真正的点，且其方向信息对于跟踪也是有用的，但通常还是把目标看作没有形状的一个点.几乎所有的机动目标跟踪方法都是基于模型的.目标M在二维平面内k时刻的状态向量用）＝［）］T来描述，其中，（，）是位移量，（，）是速度量，，）是加速度量.目标动态模型描述了目标状态X（M）随时间的演化过程，常用的离散状态空间模型的线性化形式为

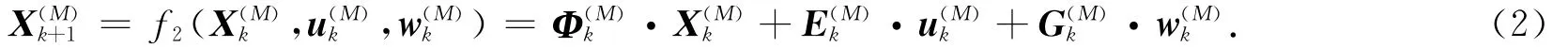
对于式（2），其具体运动模型有多种可能，从水下运动目标的运动特性上分析，最常见的运动模式为直线运动，模型分别为

Ⅰ 匀速模型（CV model）：

其中 T（M）为目标M的采样周期为k时刻过程噪声协方差矩阵的系数.

Ⅱ 匀加速模型（CA model）：

当目标发生大的机动，基本模型不能满足跟踪需要时，可以采用综合基本模型的交互多模型［12］方法跟踪复杂运动目标.

1.3 量测模型

当AUV的声纳系统探测目标M时，探测回波可提供径向距离和方位角两维量测信息，即

设νk＝ ［ΔrkΔθk］T服从高斯分布，则E［νk］＝0，E［νk（νl）T］＝Rkδkl.

量测模型可被简单地描述为

2 基于EKF-SLAM框架的SLAT算法

2.1 状态预测

在k＋1时刻系统的状态协方差的预测为

2.2 量测更新

使用k＋1时刻传感器量测更新系统状态，设在k＋1时刻利用系统状态对量测值的估计为

从而k＋1时刻的新息和新息协方差为

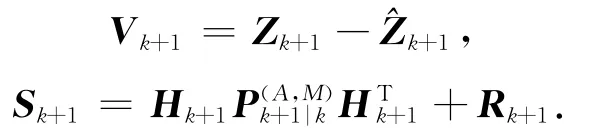
滤波器增益为

对广义状态向量及其协方差矩阵进行更新，有

其中

3 基于FastSLAM框架的SLAT算法

设定滤波器中有N个粒子，并设采样时间T（A）＝T（M），粒子i的构成可由式（3）表示.

粒子i对AUV在k＋1时刻的状态估计值可以表示

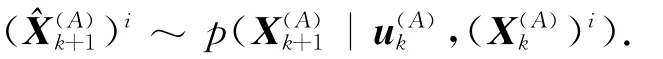
根据式（1），可得

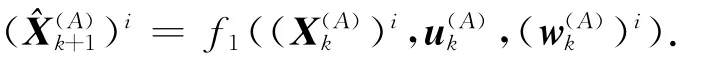
根据式（2），可以推算得到目标M在k＋1时刻的状态估计值为

在k＋1时刻目标M的状态协方差的预测为

使用k＋1时刻传感器量测更新系统状态，设粒子i在k时刻状态量对量测值的估计为

从而k＋1时刻的新息和新息协方差为

滤波器增益为

则对目标状态向量及其协方差矩阵进行更新，有

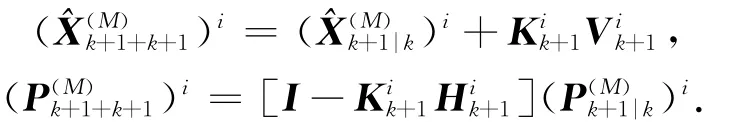
其中，

权值可表示为AUV的运动分布函数与建议分布函数之比，即

则有

归一化所有粒子的权值

则k＋1时刻AUV的位姿和目标状态估计为

为了保证粒子的有效性，估计过程中经常需要进行重抽样.判断是否需进行重抽样的指标为

Neff代表有效粒子数，当Neff小于设定最小粒子数时，需要进行重采样.根据权值大小，复制权值大的粒子，并删除权值小的粒子，最终重新抽取N个粒子，并设所有粒子权重为1／N.

4 仿真分析

为了标注简单，将基于EKF-SLAM框架的SLAT算法和基于FastSLAM框架的SLAT算法简化命名为SLATE和SLATF.设目标M和AUV沿着各自方向运动，并设定AUV可实时探测到目标M以获取相应的距离和方位信息.为了验证算法的有效性，本文仿真中将目标M的真实航迹，AUV的真实航迹和航位推算轨迹显示以比较.进行100次Monte Carlo仿真，仿真结果如图1～4所示.

图3 目标位置估计轨迹比较

图2 AUV位置估计轨迹比较

图1 目标和AUV的真实轨迹

图4 AUV位置估计的误差比较

图1 ～3为粒子N＝100时仿真结果.图1显示了目标和AUV真实的运动轨迹关系.在运动过程中，AUV与非合作目标体之间无通信联系，通过AUV携带的声纳系统实时探测目标体得到目标的距离与方位信息.图2显示了AUV真实运动轨迹、航位推算结果、SLATE和SLATF的估计结果，SLATE的估计效果明显优于航位推算，而SLATF与运动轨迹真值的复合度最高，优于SLATE.图3显示了目标M的真实轨迹，SLATE和SLATF的航迹估计结果.从估计值与真值的复合程度来看，SLATF对非合作目标体位置量有一个更好的估计，表明了算法的有效性.图4～6对AUV的航位推算，SLATE和粒子数N取不同值时的SLATF估计误差作了比较.随着时间的推移，航位推算系统的累积误差越来越大，而SLATE和SLATF能有效地抑制误差在一个合理的水平内，证明估计航迹时本文提出的方法明显优于航位推算，而SLATF优于SLATE.横向比较图4～6中SLATF的估计误差曲线可以看出，随着使用粒子的增多，估计误差有变小的趋势，说明足够的粒子可以提升估计器的性能，但提升水平相对有限.

在理想情况下，衡量算法是否满足一致性是将其估计值与理想滤波器中获取的概率密度函数进行比较.在实际中理想概率密度函数是无法获取的，但当被估计状态真值已知时，可以使用标准化估计误差方差（normalized estimation error squared，NEES）测试滤波一致性.图5中两种SLAT算法NEES的均值基本位于置信区间中，说明了估计过程具备一致性.

图5 AUV位姿NEES均值

5 结束语

本文将AUV运动的推算模型、量测模型与目标运动的跟踪模型融合于EKF-SLAM框架和FastSLAM框架内，提出了两种AUV跟踪目标同时自定位的方法.在基于EKF-SLAM框架的SLAT中，虽然目标和AUV的运动状态会相互依赖和影响，但将二者统一在一个广义状态向量中，状态估计误差间相关性带来的影响可以通过协方差矩阵在滤波器中消除.而对于植入粒子滤波器的基于FastSLAM框架的SLAT，具有更优的估计效果，更好地解决了边跟踪边自定位问题.从仿真结果中可以看出，两种SLAT方法不但AUV自定位的累积误差相比于航位推算减小很多，而且同时也能对非合作目标的航迹有较准确的估计.

［1］ CURCIO J，LEONARD J，VAGANAY J，et al.Experiments in moving baseline navigation using autonomous surface craft［C］／／Proceedings of 2005MTS／IEEE International Conference on OCEANS，Washnigon DC，IEEE，2005：730-735.

［2］ GADRE A S，STILWELL D J.Toward underwater navigation based on range measurements from a single location［C］／／Proceedings of 2004IEEE International Conference on Robotics and Automation，New Orleans，IEEE，2004：4472-4477.

［3］ 许真珍，封锡盛.多 UUV协作系统的研究现状与发展［J］.机器人，2007，29（2）：186-192.

［4］ MACZKA D K，GADRE A S，STILWELL D J.Implementation of a cooperative navigation algorithm on a platoon of autonomous underwater vehicles［C］／／Proceedings of 2007MTS／IEEE International Conference on OCEANS.Vancouver BC，Canada：IEEE，2007：1-6.

［5］ BAHR A，LEONARD J.Cooperative localization for autonomous underwater vehicles［J］.Autonomous Robots：Proceedings of Experimental Robotics，2006，39（5）：387-395.

［6］ VAGANAY J，LEONARD J J，CURCIO J A，et al.Experimental validation of the moving long base-line navigation concept［C］／／Proceedings of 2004IEEE／OES International Conference on Autonomous Underwater Vehicles Nagoa，Japan：IEEE，2004：59-65.

［7］ BAKER B N，ODELL D L，ANDERSON M J，et al.A new procedure for simultaneous navigation of multiple AUVs［C］／／Proceedings of 2005MTS／IEEE International Conference on OCEANS，Washnigon DC：IEEE，2005：1-4.

［8］ XU W M，LIU Y C，YIN X D.Method for underwater target tracking based on an interacting multiple model［J］.Geospatial Information Science，2008，11（3）：186-190.

［9］ El-Shafile A，OSMAN A，NOURELDIN A，et al.Performance enhancement of underwater target tracking by fusing data of array of global positioning system sonobuoys［J］.Journal of Computer Science，2009，5（3）：199-206.

［10］ RAO S K，MURTHY K S L，RAJESWARI K R.Data fusion for underwater target tracking［J］.IET Radar，Sonar and Navigation，2010，4（4）：576-585.

［11］ LI X R，JILKOV V P.Survey of maneuvering target tracking—partⅠ：Dynamic model［J］.IEEE Trans.on Aerospace and Electronic Systems，2003，39（4）：212-235.

［12］ LI X R，JILKOV V P.Survey of maneuvering target tracking—partⅤ：Multiple-model methods［J］.IEEE Trans on Aerospace and Electronic Systems，2005，41（4）：1255-1321.

［13］ BLACKMAN S S.Multiple hypothesis tracking for multiple target tracking［J］.IEEE Trans on Aerospace and Elec-tronic Systems Magazine，2004，19（1）：5-18.

［14］ THRUN S，BURGARD W，FOX D.Probabilistic Robotics［M］.Lodon：MIT Press，2005：52-60.

［15］ BAILEY T，NIETO J，GUIVANT J.Consistency of the EKF-SLAM algorithm［C］／／Proceedings of 2006IEEE／RSJ International Conference on Intelligent Robots and Systems.Beijing：IEEE，2006：3562-3568.

［16］ LAZARO M T，CASTELLANOS J A.Localization of probabilistic robot formations in SLAM［C］／／Proceedings of 2010IEEE International Conference on Robotics and Automation.Anchorage AK：IEEE，2010：3179-3184.

［17］ Durrant-Whyte H，BAILEY T.Simultaneous localization and mapping：partⅠ［J］.IEEE Robotics and Automation Magazine，2006，13（2）：99-110.

［18］ BAILEY T，DURRANT-WHYTE H.Simultaneous localization and mapping：partⅡ［J］.IEEE Robotics and Automation Magazine，2006，13（3）：108-117.

［19］ DISSANAYAKE M W M G，NEWMAN P，CLARK S，et al.A solution to the simultaneous localization and map building （SLAM）problem［J］.IEEE Transactions on Robotics and Automation，2001，17（3）：229-241.