导航定位专业中几个与精度相关的术语辨析

2014-01-10许丽丽刘英乾杨文彬

导航定位学报 2014年3期

许丽丽，刘英乾，杨文彬，夏天

（北京东方计量测试研究所，北京 100086）

1 引言

国内导航领域广泛使用 “精度”（精确度precision的简称）术语表征导航定位特性，但国际导航领域相关标准和技术文献中均使用英文 “accuracy”（在相关国家标准中译为 “准确度”）表达相应特性；而在对 “accuracy”特性的描述中，导航业内存在着概率包含区间、标准偏差（或其特定倍数）、均方根误差等多种表示方式，且在这些表示方式的认识和使用上存在着一定的混乱。与此同时，在计量领域更多采用测量不确定度表达测量仪器的准确度特性，并以其对测量仪器进行合格评定或确定准确度等级。这些来自不同专业领域的关于准确度的不同表示方式，给从事导航设备检测校准工作的技术人员带来了相当的困惑。

本文作为一次沟通不同专业领域技术术语的努力，意在对目前国内导航领域常用的 “精度”一词进行辨析，力图使用规范的术语 “准确度”表达导航特性，并对 “准确度”的不同表示方式及其数据处理方法给予说明。

2 准确度相关术语

在几个等同采用或参考采用国际相关标准的我国国家标准及校准规范中，对 “准确度”及相关术语均给出了定义［1－3］，如表1所示。

由上述定义可以看出，在不同的国家标准和校准规范中，对准确度相关术语的定义并不完全一致。

在国家标准《GB／T 3358.2—2009统计学词汇及符号第2部分：应用统计》（idt ISO 3534—2：2006）和《GB／T 6379.1—2004测量方法与结果的准确度（正确度与精密度）第1部分：总则与定义》（idt ISO 5725—1：1994）中，准确度、正确度和精密度仍然可以进行定量表达：

（1）用术语 “准确度”表示的测量结果，包含了系统误差分量和随机误差分量；准确度是正确度和精密度的结合。

（2）术语 “正确度”表示测量的系统误差，一般用偏倚（bias）——重复测量的误差平均值来估计。

（3）术语 “精密度”表示测量的随机误差，其量值用测试结果的标准差来表示。

在测量实践中，系统误差可以修正，而随机误差则不能修正，随机误差的分布范围影响着测量结果的可信度。

而在国家校准规范《JJF 1001—2011通用计量术语及定义》（依据ISO／IEC GUIDE 99：2007最新修订）中：

（1）准确度、正确度不再作为定量概念。

（2）精密度则只用于定义测量重复性、期间测量精密度或测量复现性，并明确指出用精密度指代准确度是错误的。

表1 相关国家标准／校准规范中对准确度相关术语的定义

（3）不确定度用于表征被测量量值分散性，由若干不确定度分量组成，用标准偏差（或其特定倍数）表示。

事实上，在计量学术领域，更多采用测量不确定度（简称 “不确定度”）给出测量仪器的准确度特性或评定其准确度等级［4－5］，且已被仪器制造行业广泛接受。

显然，术语 “准确度”并不能用术语 “精（密）度”代替，而在报告测量结果的准确度时，依据GB／T 6379.1—2004，一般要同时报告正确度（或称 “偏倚”，一般称为 “偏差”）和精（密）度；或者依据《JJF 1059.1—2012测量不确定度评定与表示》，同时报告被测量的估计值及其测量不确定度以及有关信息。后一种报告方式既是目前计量领域的学术要求，也是国家法制化计量的要求。

3 准确度特性的表征

目前广泛使用的导航准确度特性有三种表征方式：

1）以标准偏差σ表示的准确度指标［6］，如1σ、2σ；

2）以概率包含区间表示的准确度指标，如CEP、SEP、95%概率误差（的包含区间）等；

3）以均方根误差表示的准确度指标。

其中，前两种指标给出的是对随机误差的度量；均方根（root mean square，RMS）误差则包括了系统误差和随机误差。

在导航定位应用中，不同厂商的导航定位产品可能会采用上述不同的表征方式给出产品的准确度特性，因此，需要在不同的表征方式间建立数学关系，才能对产品的技术指标进行对比。在本文中，将以定位准确度指标为例，说明如何在不同的导航准确度表示方式间建立数学关系，对于其他导航准确度特性如速度准确度，可以按照相同的方式处理。

考虑到导航准确度常用于表示导航定位接收设备的关键技术指标，其测量方法、测量结果的报告以及准确度等级评定应遵循相关的国家校准规范，对如何计算定位结果及评定其不确定度亦将在下文予以讨论。

3.1 以标准偏差表示的准确度

标准偏差（standard deviation）又称标准差，是随机变量分散程度的表征，对于随机变量x，其标准差s的定义式为

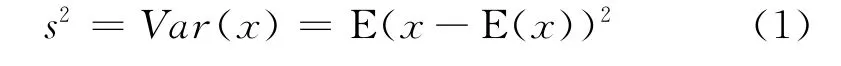
对于较大样本（n≥6 的测量值（随机变量）x，其标准偏差s的估计值——实验标准偏差σ一般用贝塞尔公式计算

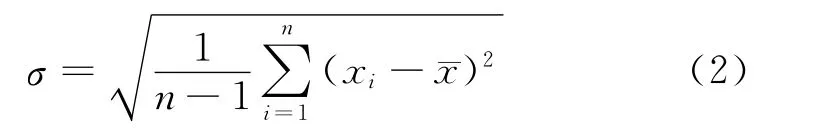
标准偏差（或其特定倍数）用于表示导航定位准确度指标时，可以对定位误差向量在直角坐标系下各方向的分量分别应用式（2），得到标准偏差的各方向分量，再通过向量合成得到多维标准偏差［4］。

例如，在站心坐标系（NEU，北、东、天方向）下，计算n次（已选择适宜的数据剔除准则对定位数据进行剔除后）定位测量数据的水平误差（1σ）和高程误差（1σ）的方法如下：

1）计算在站心坐标系下第i个实时定位数据（Ni，Ei，Ui）在各方向的定位误差（ΔNi，ΔEi，ΔUi），其中（N0i，E0i，U0i）为第i个实时定位的标准点坐标

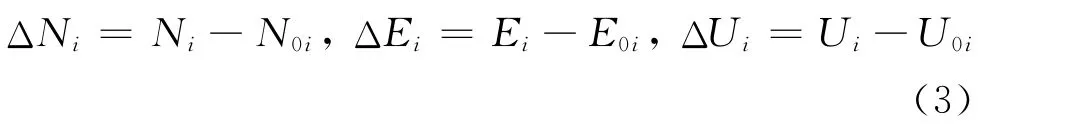
2）计算定位偏倚（bias，一般译为 “偏差”，即系统误差）的各方向分量为

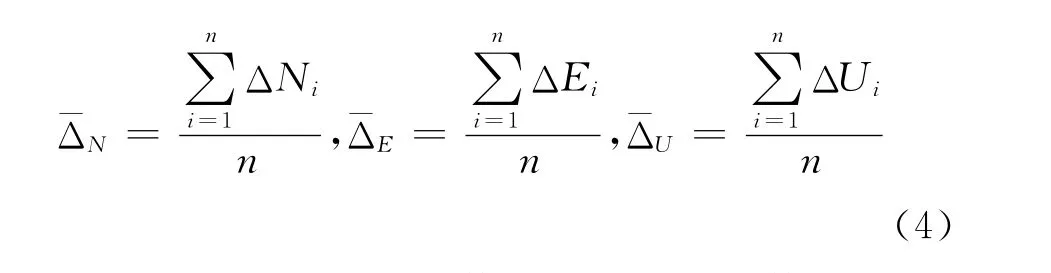
3）计算标各方向误差分量的标准偏差为

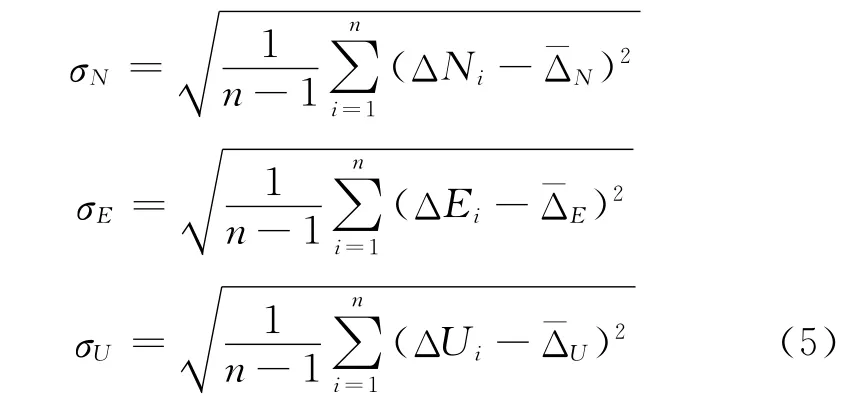
4）计算水平标准偏差σH、三维标准偏差σ3d

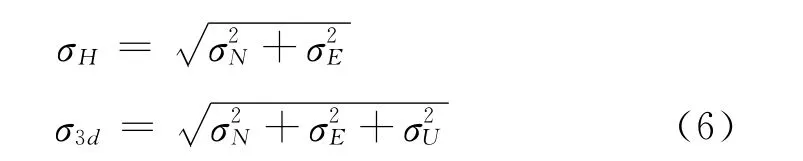
3.2 以概率包含区间表示的准确度

是基于落在一定的区间（一维）、面积（二维）、体积（三维）内的随机误差均有特定的概率而定义的导航准确度指标，例如CEP（圆概率误差）是指二维随机误差以50%的概率落在其内部的误差圆之半径，R95则是95%概率误差圆的半径，而SEP（球概率误差）则是三维随机误差以50%的概率落在其内部的误差球之半径［7］。

在误差数据的处理上，需要基于误差的统计分布等假设，对该指标进行计算。

设在直角坐标系下测得一组定位数据（xi，yi，zi），其标准点坐标为（xo，y0，z0）。假设定位误差各方向分量不相关且均服从正态分布，即：x～N（μx，σ2x）、y～N（μy，σ2y）、z～N（μz，σz2）。其中：μx、μy、μz分别为定位误差各方向分量的数学期望（即平均值）；σx、σy、σz为定位误差各方向分量的标准偏差。

因n个服从标准正态分布的独立随机变量的平方和服从自由度为n的χ2分布［9］，即有

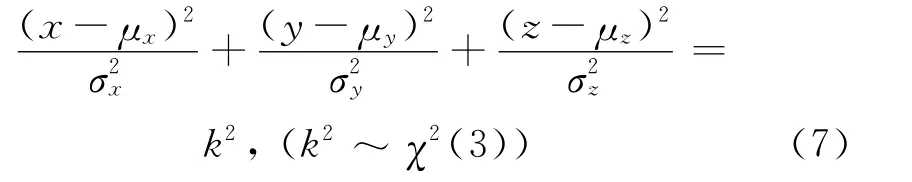
由此可知，对于三维定位误差，概率为p（基于χ2（3）分布可计算其对应的k2值）的点分布在一个中心为（μx，μy，μz），三轴分别为σx、σy、σz的误差椭球内，该椭球的方程为式（7）。

同理，对于二维定位误差，概率为p的点分布在一个误差椭圆内，椭圆方程为

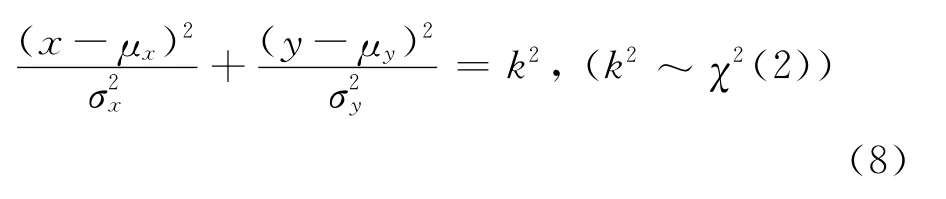
表2给出了不同维度下典型概率p对应的包含因子k，其中一维情况下，χ2分布退化为正态分布。

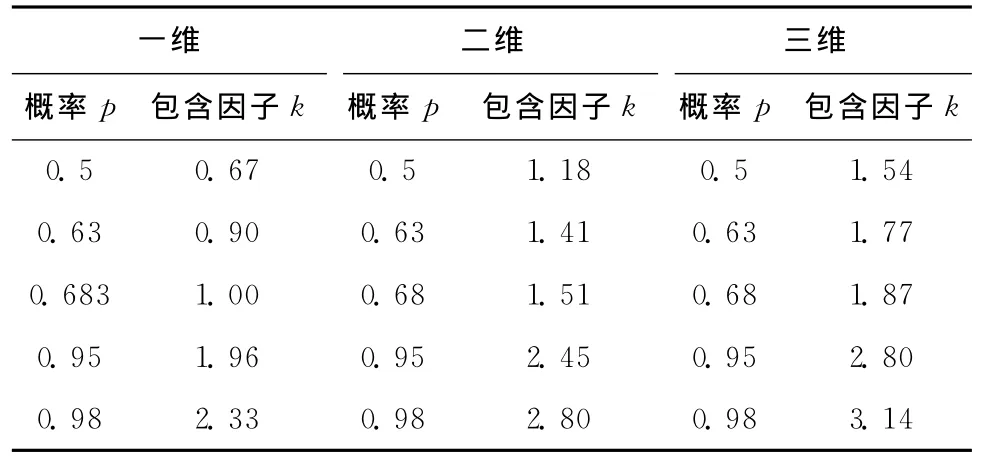
表2 概率与包含因子对照表

对于一维定位准确度指标，如高程的95%概率误差包含区间，由表2有U95＝1.96σU，其中σU为高程误差的标准偏差，由式（5）计算得到。

对于二维或三维定位准确度指标，表2给出了概率p对应的误差椭圆（球）各轴长度与定位误差各方向分量标准偏差间的转换因子k。不过，一般情况下更希望得到的是相同维度下不同准确度指标之间的转换关系，例如水平定位标准偏差σH与概率为p的水平定位误差圆半径Rp之间的关系。如此，为简化计算，假设误差椭圆（球）的轴比近似为1，即σx＝σy（＝σz），则误差椭圆（球）退化为误差圆（球）［9－10］。

例如，在站心坐标系（NEU坐标系）下对水平定位准确度指标应用上述各关系式，有

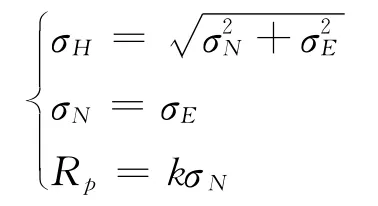
故

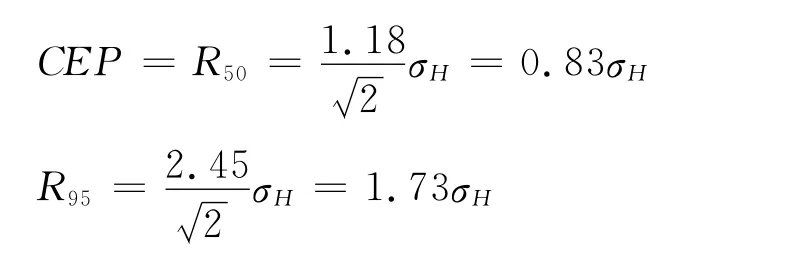
对于水平方向，在随机误差接近正态分布，且误差椭圆轴比约为1的假设下，可取放大系数2.448／≈1.74，或取其安全的近似值2（水平误差落在半径为2σH的圆内的概率在95.4%～98.2%之间，具体值取决于误差椭圆的轴比，2σH值通常作为水平误差大小的95%界限［7］）

3.3 以均方根误差表示的准确度

测量值x的均方根误差定义［11］为

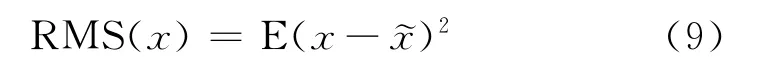
其中，为x的真值，注意其与标准偏差定义式（1）的区别，标准偏差给出的是测量值与其平均值之差的平方和的均值，而RMS给出的是测量值与真值之差的平方和的均值。

事实上，可以证明［10］

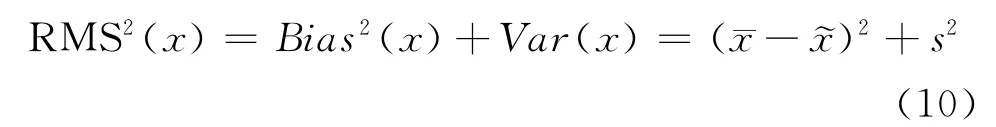
即测量值x的均方根的平方等于其偏倚Bias（x）与标准差s（常用其估计值σ表示）的平方和，其量值中同时包含有系统误差和随机误差。

式（10）常用于间接测量时RMS指标的计算，举例如下

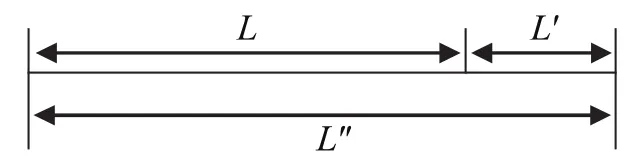
图1 间接测量示例

假设对于待测量L，只能通过测量L″和L′后求差得到，即有

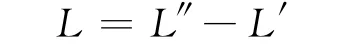
分别对L″和L′进行多次测量，得到测量值L″i和L′ii＝12n由误差传播规律有（假设L″与L′不相关）

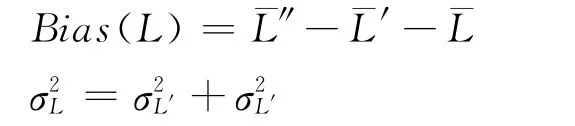
其中，和分别为L″i和L′i的平均值，为L的理论真值，σL″和σL′分别为其标准偏差。

由式（10）有

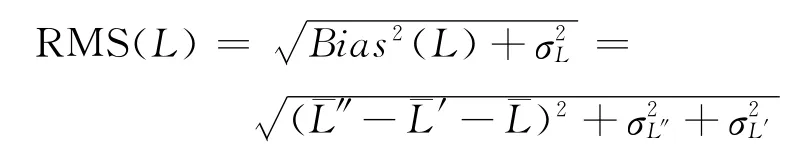
需要指出的是，式（9）给出的均方根误差由其定义而来，系由高斯提出，并被国内导航、测绘领域采用。但在国外科技文献中，类似国内业界的RMS用法并不常见［5］，一般将RMS与标准偏差σ混用，例如在本文的三篇外文参考文献［7，9－10］中，均给出类似于的表达，显然，将DRMS等同为二维标准偏差。为便于讨论，本文未采用上述国外文献对RMS的使用方式，仍沿用了国内学术惯例。

3.4 以不确定度表示的准确度

依据国家校准规范《JJF 1069—2007法定计量检定机构考核规范》的要求，法定计量机构开展各种类型的检定、校准和检测业务，均应按照JJF1059进行不确定度评定并予以报告，但目前在导航领域，不确定度并未得到广泛应用。

不确定度是测量结果分散性的表征，用标准偏差（或其倍数）表示，由未修正的系统误差分量以及各种随机误差分量合成得到［5］。下面仍就3.1给出的示例，说明如何用GUM法对水平定位测试结果的不确定度进行评定。

计算方法见式（4）。

2）分析各坐标轴（N、E）方向定位误差的标准不确定度

首先以N向为例进行计算。

N向定位误差的标准不确定度主要由三个分量构成：由重复性引入的不确定度分量uNA、由测量标准（标准点位）引入的不确定度分量uNB1、由被测导航接收设备的分辨力引入的不确定度分量uNB2，分别计算为

（1）对于由重复性引入的标准不确定度分量uNA，采用A类评定方法（统计方法）。对于n次重复测量得到的定位误差结果（即误差的算数平均值）的标准偏差，有

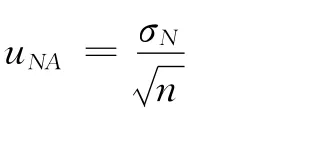
（2）对于由标准点位的坐标误差（各方向均不超过a）引入的标准不确定度分量uNB1，采用B类评定方法，假设标准点位误差为均匀分布，则

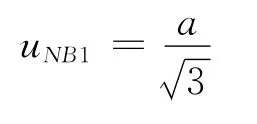
在一般的导航应用中，导航接收设备的定位准确度一般在米级以上，而标准点位坐标的各方向的误差a均可以在分米级以下，对于准确度为米级以上导航设备，该分量小于总标准差的的1／3，根据微小误差的取舍准则［12］，该分量可以不予考虑。

（3）对于由被测导航接收设备的分辨力引入的标准不确定度分量uNB2，导航接收设备的位置分辨力一般在经纬度方向上均优于0.001′，经计算可知，分辨力在N、E方向上均不超过2m，故

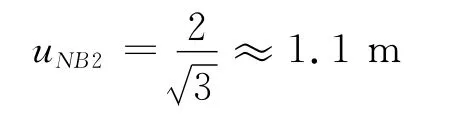
由上，可得到N方向定位误差的标准不确定度uN

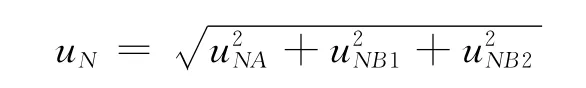
同理，可分析E方向定位误差的标准不确定度uE。

由N、E方向的不确定度分量，得到水平定位误差的标准不确定uH

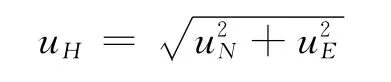
3）计算定位误差的扩展不确定度UH

一般情况下，取包含概率95%，基于3.2的分析，在服从二维正态分布的假设下，不确定度椭圆对应的包含因子k＝2.45，在不确定度椭圆的轴比为近似为1时，包含概率95%的不确定度圆的半径U95为

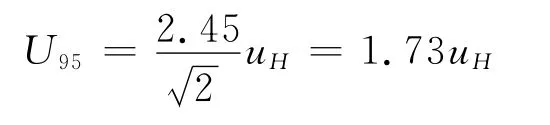
一般扩展系数取其安全的近似值2，即

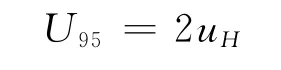
4）定位误差测量结果的报告

4 结束语

在卫星定位导航领域，建议与国际学术惯例保持一致，使用 “准确度”而不是 “精度”表达导航特性。导航准确度特性是导航精（密）度和导航正确度的结合，一般而言，用准确度表示的测量结果由随机误差分量（由精密度表示）和系统误差分量（由正确度表示）组成。系统误差是可以修正的，而随机误差不可修正，其分散性影响测量结果的可信度。

在目前导航领域的实际应用中，导航准确度有三种广泛使用的表征方式：以标准偏差表示的准确度、以概率包含区间表示的准确度、以均方根误差表示的准确度。基于特定的统计分布等假设，可以在不同的准确度表示方式间建立数学关系，以对不同方式给出的准确度特性进行比较。

基于计量领域的学术要求和国家计量技术法规的要求，卫星导航业界未来也许会更多地采用测量不确定度表征导航定位设备的导航准确度指标，并以此进行合格评定或评定准确度等级。本文可以视为一次沟通不同专业领域技术术语和方法的尝试，期待与业界同仁共同商榷，不当或谬误之处敬请指正。

［1］ GB／T3358.2—2009，统计学词汇及符号第2部分：应用统计［S］.

［2］ GB／T6379.1—2004，测量方法与结果的准确度（正确度与精密度）第1部分：总则与定义［S］.

［3］ JJF1001—2011，通用计量术语及定义［S］.

［4］ JJF1094—2002，测量仪器特性评定［S］.

［5］ JJF1059.1—2012，测量不确定度评定与表示［S］.

［6］赵芹，杨俊志.测量准确度及相关术语辨析［J］.测绘科学，2011，36（1）：75－76，89.

［7］ NATO STANAG4278－1995，Method of Expressing Navigation Accuracies［S］.

［8］周江文.误差理论［M］.北京：测绘出版社，1979：109－119.

［9］ VAN DIGGLEN F.GNSS Accuracy Lies，Damn Lies，and Statistics［J］.GPS World，2007（January）：26－32.

［10］ KAPLAN E D，HEGARTY J.Understanding GPS Principles and Applications［M］.2nd.Boston：Artech House，2006：328－332.