协同定位中用户可定位性分析

刘亚宁，李广侠，常 江，田世伟，刘 冰

（1.解放军理工大学 通信工程学院，南京 210007；2.中国科学院 光电研究院，北京 100094）

1 引言

目前，全球卫星导航系统（global navigation satellite system，GNSS）由于具有精度高、覆盖范围广以及可全天候工作等优势，已成为应用最为广泛的导航定位技术。在开放环境中，基于GNSS的单点定位技术相对成熟，定位精度也在不断提高。一般情况下，只要地面节点能够收到4颗及4颗以上卫星的信号，都能够实现单点定位［1－7］。但在一些恶劣环境下，如室内、城市峡谷以及森林等一些被遮蔽的环境，由于缺少足够多的可见卫星，单点定位无法实现。

协同思想在人类社会中源远流长，协同学作为一个科学概念被正式提出是在20世纪70年代。在生物学领域，协同进化能大大加快生物进化的历程；在计算领域，协同进化算法为研究者开辟了广阔的空间；在通信领域，协同不仅能提高单个设备的传输效果，而且能够显著提升无线系统的整体性能。鉴于协同思想在其他领域所取得的成果，定位导航领域也出现了协同定位的概念。

协同定位的概念最早由文献 ［8］在1996年提出，主要用于实时获取移动机器人的位置信息。其主要做法是，将机器人编为两个组，一个组移动的时候，另一组作为地标保持静止，辅助前一个组的移动。在实验过程中，两个组再不断交换角色，直至到达目标位置。如今，节点之间的协同定位概念已经延伸到利用节点之间的通信及测量信息等辅助单个节点定位。相比增加 “伪卫星”、锚节点的高代价，协同定位不仅开销小，而且能缩短首次定位的时间，提高单点定位的精度，提高系统的鲁棒性，改善整个系统的定位性能。协同技术在定位领域中的许多方向已经取得了一定的成果，如无线传感网（wireless sensor network，WSN）定位［9］、多机器人协同定位［10］等。在卫星定位中，关于协同技术的研究尚不是很多，主要集中在协同定位的理论定位精度及一些协同定位算法，文献 ［11－12］做的研究工作具有代表性，此外，节点的可定位性也有了一定的研究［13］。

传统的GNSS定位研究主要考虑的是单点定位问题。关于单点定位下的位置解算，文献 ［3］于1984年提出了一种解法。基于Lorentz内积公式，文献 ［3］提出了一种伪距方程组的矩阵解法。该解法计算效率高，并且不需要初始位置信息，定位方便、快捷。与此算法类似，本文提出了一种在两点协同场景下的定位算法。

本文研究协同定位中的一个具体场景：两点协同模型，以更好地对协同定位问题进行理解。通过假设两个未知节点之间可以相互通信及测量，能够得到节点之间的高程差信息以及相对距离信息。同时利用用户解算出的其与卫星之间的伪距信息，本文提出了一种新的算法，能够同时解算出两个节点的实际位置以及它们与卫星时钟的钟差。本文的主要贡献是分析并证明了单个不能定位的用户通过协同能够实现定位，同时，分析了协同定位的可定位性，为以后的多点协同定位以及整个网络的协同定位的研究提供了参考。

本文内容安排如下。第二部分回顾了用户单点定位的模型，并总结了目前存在的几种解法，同时对各种解法之间的差异以及他们的优势进行了比较。考虑到一些恶劣环境中，可见卫星少，单点定位可能无法实现。本文第三部分研究了协同定位中的一个具体场景：两点协同定位。并建立了协同模型，设定了协同的形式及内容。第四部分为理论证明工作，证明了两个原本都不能实现定位的节点，经过协同，能够实现定位。用户可定位性提高的仿真证明出现在第五部分。第六部分为本文总结及下一步的工作。

2 单点定位回顾

2.1 单点定位原理

GNSS单点定位利用地面单个用户接收到的卫星信号，通过对信号进行处理和解算，得到卫星的精确坐标以及卫星与用户之间的伪距信息。根据接收到的一组伪距建立伪距方程组，并对方程组进行求解得到用户的3维坐标以及钟差。由于有4个未知数，必须要有4个或4个以上方程组，即单点能接收到4颗及以上卫星的信号如图1所示时，才有可能得到一组解。

图1 用户至少能接收到4颗卫星的信号

2.2 单点定位的几种解法

单点定位问题从20世纪80年代起，得到了很多学者的关注，经过30多年的研究，出现了一大批研究成果［1－7］。下面将对这些方法进行比较，给出它们的差异以及各自的优势。

文献 ［1－2］是一种全球定位系统（global positioning system，GPS）伪距方程的迭代解法。通过估计用户的初始位置，运用牛顿迭代法，经过3到5次迭代，就能得到用户的精确位置。这种方法易于理解，但计算量较大，第一次定位时初始位置不容易估计，同时，在深空等其它环境还可能收敛到一个错误的解。

文献 ［3－7］提出了伪距方程的代数解。基于Lorentz内积公式，文献 ［3］提出了一种GPS伪距方程的代数解，该解法思路清晰，计算简单，不需要估计初始位置，但文献 ［6］已经证明了，即使在卫星星座条件非常好的情况下，运用这种解法，也可能得到多个解。基于线性差分方法，文献 ［4］利用测得的用户与卫星之间的距离差，经过矩阵变换、求逆，能够得到一组代数解。该解法计算过程较复杂，但由于矩阵求逆的最高阶为二，相对于上一种方法，计算量较小。

文献 ［5］讨论了GPS方程解的存在性和唯一性条件。通过该文献知道，在接收到4颗卫星的情况下，解的存在性和唯一性都不能保证。即使在有5颗卫星的情况下，考虑到卫星可能存在的共面情况，解的唯一性也不能保证。这为接收机的设计者提供了一个很好的提示，在一些特殊情况下，为了实现准确定位，需要额外的伪距信息或者其它信息来辅助定位，这也为协同定位提供了一个很好的应用场景。文献 ［6］对比了距离方程和伪距方程。考虑到伪距方程中用户与卫星之间的钟差，不同的钟差会导致卫星－用户之间的几何学构型的不同。该文献阐述并证明了距离方程是欧式距离方程，而伪距方程是欧式距离差方程。求解距离方程用的是球面或者平面交点法，而伪距方程是旋转双曲面交点法。通过将方程解分为线性解和非线性解两部分，本文献还讨论了方程组解的稳定性。通过将双曲面之间的交线问题转化为双曲面和平面之间的交线问题，文献 ［7］从三维角度提供了一种伪距方程的解法。该解法适用于卫星星座退化等其他特殊场合，同时还能分析定位解存在性和唯一性条件。

2.3 从单点定位到多点协同定位

以上分析了单点定位的原理以及针对伪距定位方程的多种解法。但对于许多恶劣环境，由于缺少足够多的可见卫星，单点定位无法实现。在一些受到有意无意干扰的环境中，单点定位的可行性和准确性也无法保证。同时，当用户处于深空中或者靠近卫星时，单点定位也可能出现错误的结果［14］。

在这些需求的刺激下，多点协同定位应运而生。通过协同，可以得到几个用户之间的距离、时钟差、信噪比以及多普勒频移等信息［15］。在这些信息的辅助下，可以使原本不能定位的单个节点在经过几个点之间的协同之后，能够实现定位。

本文就协同定位中的一个具体场景，两点协同的模型，进行了分析和讨论。本文假设两个用户之间能够测得距离信息，同时还假设用户之间时钟差信息先验已知。通过建立协同模型，以及对模型的分析求解，可以得到两点的协同解，以及解的存在和唯一性条件。

3 模型建立

从文献 ［5］可知，用户收到5颗及以上卫星信号，一般都能实现定位，收到4颗卫星信号时，可能有多个定位解也可能无解，因此，必须对接收卫星的星座结构进行分析，判定是否能够实现定位。若用户收到少于4颗星，如3颗，单个用户本身不能定位。本场景考虑两个用户各能收到3颗星，且这3颗星互不相同，通过两点的测距和通信，判断是否能够实现定位。

如图2所示，A、B两用户均只能接收到3颗卫星的信号。按照传统的卫星定位方法，由于缺少足够的条件，两个用户均不能实现定位。协同定位的思想如图3所示。在这种场景中，两个用户除了接收卫星信号外，还能通过自身其他的硬件设备，实现测距和通信。通过两者之间的信息交互，可以得到它们之间的距离以及时钟差。在第四部分中，就将证明，通过用户之间的协同，两个原本都不能定位的用户能够实现定位。同时，第四部分还分析了用户不能定位的条件，对协同可定位性进行了初步分析。

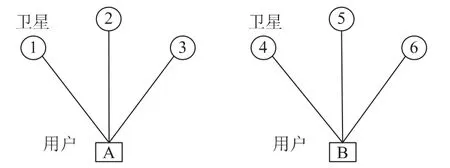
图2 用户A、B单独工作时，均不能定位

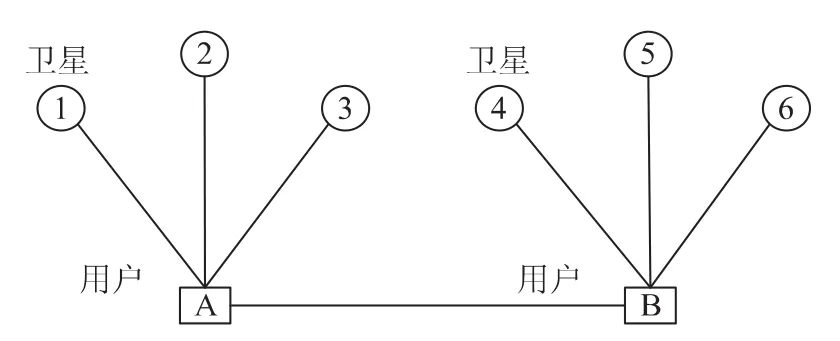
图3 通过协同，A、B两用户均能定位

在上面两个图中，①、②、③，④、⑤、⑥表示用户能看到的两组卫星，A，B表示两个用户。设xi，yi，zi（i＝A，B，1…6）分别表示各点的坐标，ti（i＝1…6）表示卫星到用户之间的伪距，用户A与各卫星之间的钟差为b1，用户B与各卫星之间的钟差为b2，通过协同，A与B之间的时钟差已知，即b1＝b2＋c，c为常数，同时A与B之间的距离h也已知。

4 模型的求解

由卫星伪距方程知道，对于用户A有以下方程成立

同样对于用户B，有

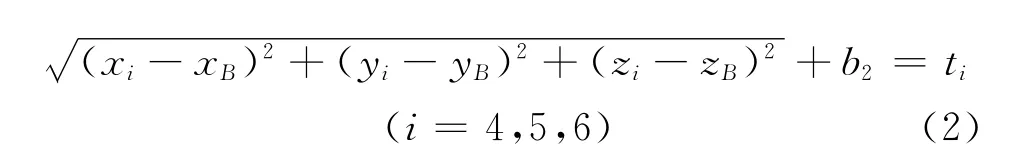
另外，通过A、B之间的测距以及通信，可以得到另外两组关系式

将方程（1）移项，展开得

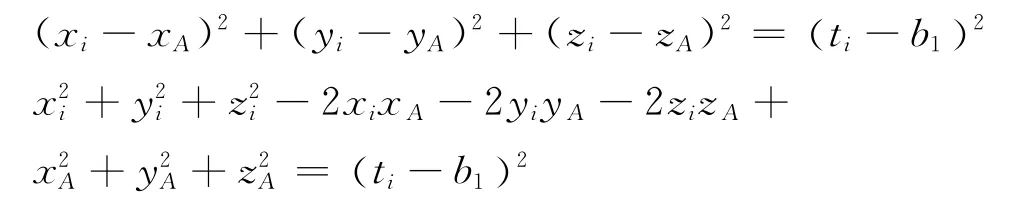
令矩阵

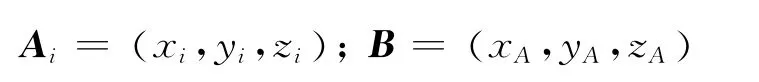
则上式可以表示为

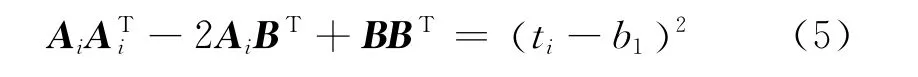
由上式可知，i＝1，2，3时有三个方程。

联立以上三个方程式，得到一个用矩阵表示的方程

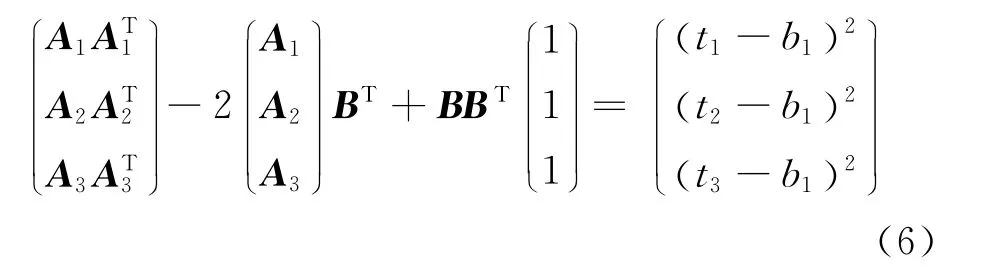
设BBT＝λ则

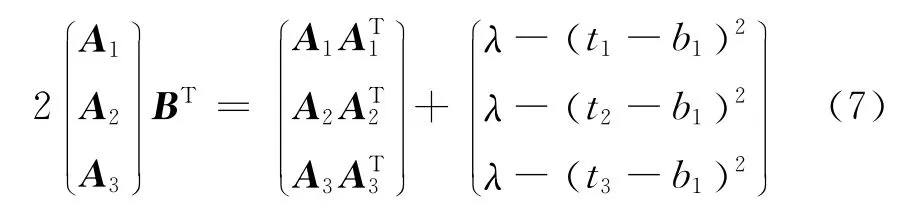
从（7）式可以得到

此处进行协同定位可定位性的第一次判断，若三维矩阵（A1A2A3）T可逆，则能够实现协同定位，若三维矩阵（A1A2A3）T不可逆，则说明这3颗卫星的星座结构不理想，不能实现协同定位。

将式（8）代入BBT＝λ，可以解出未知数λ，再将λ代到式（8），可以得到B，从而可以得到xA，yA，zA与b1之间的关系。同理，由式（2）可以得到xB，yB，zB与b2之间的关系。将xA，yA，zA与b1之间的关系，xB，yB，zB与b2之间的关系代回到

可以得到一个b1与b2之间关系式。

又因为b1＝b2＋c，由以上两个b1与b2之间关系式，通过解二元一次方程，可以解出b1与b2的值，再将它们代回到xA，yA，zA与b1之间的关系式以及xB，yB，zB与b2之间的关系式中，可以求得xA，yA，zA与xB，yB，zB的具体值，即能够实现对两个用户A与B的定位。

此处进行协同定位的第二次判断，若方程组有解，则表示能够进行协同定位，若方程组无解，则说明这6颗卫星星座结构不理想，不能进行协同定位。

5 仿真验证

为了研究协同定位的可定位性性能，考虑两个用户协同定位的情况，本文将分别分析两个用户非协同定位以及协同定位的场景。在仿真中，假设A、B两个用户所处的经纬度坐标分别为（116.218，35.33），（116.318，35.43）。由 于 森林覆盖或者高楼阻挡等原因，假设A、B各能接收到三颗卫星的信号，分别为GPS＿BIIA－22、GPS＿BIIA－27、GPS＿BIIR－06以及 GPS＿BIIA－25、GPS＿BIIRM－5、GPS＿BIIRM－2，如图4所示。仿真时间为 2013－07－02T09：20：00—11：00：00。在仿真中，每60s记录一次卫星的位置以及用户与卫星之间的距离信息。同时，如果仿真中测得的用户位置与用户的真实位置误差小于10m时，认为用户是可以定位的。

图4 用户协同定位场景

图5比较了协同定位和非协同定位情况下用户的可定位性。在非协同定位场景中，由于每个用户单独定位且只能接到3颗卫星的信号，而这里有4个待求解量（即用户的三维坐标x，y，z以及钟差b），显然，用户不能被定位。在协同定位场景中，用户不仅能接收到卫星信号，用户之间还能通过协同得到额外的定位信息观测量，如用户之间的时钟差、用户之间的距离等。仿真结果证明，协同定位可以很大程度提高用户的可定位性。当协同用户组数增加到500时，用户的可定位性可以提高到98%。

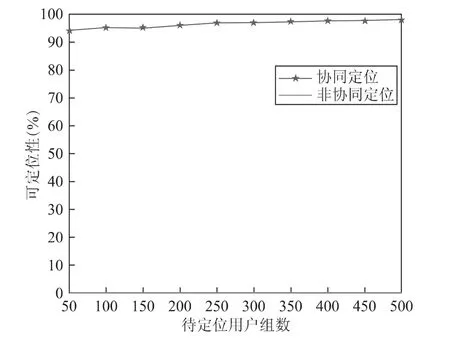
图5 协同与非协同场景下用户可定位性比较

6 总结及进一步研究方向

本文回顾了单点定位的模型，总结了单点定位存在的几种解法，并对他们进行了对比，分析了各自的优势。就卫星协同定位中的一个具体场景：两个用户的协同，建立了用户之间通过测距和通信进行协同的模型，分析了用户的可定位性，给出了定位解。本文为多用户协同定位中可定位性的分析提供了参考。

下一步会进一步研究和探讨两点协同定位。在协同的内容和方式上，会考虑更容易实现，更便于计算的方法，还要确保能够达到更高的定位精度。同时，还会将两点协同定位扩展到多点协同定位，并最终将考虑整个网络的协同定位中可定位性的问题。

［1］ MAO Xu－chu，WADA M，HASHIMOTO H.Nonlinear Iterative Algorithm for GPS Positioning with Bias Model［C］／／Proceedings of the 7th International IEEE Conference on Intelligent Transportation Systems.Washington，WA：IEEE，2004：684－689.

［2］ MARTIN E H.GPS User Equipment Error Models（User Equipment）［J］／／Navigation，1978，25（2）：201－210.

［3］ BANCROFT S，KING R D.An Algebraic Solution of the GPS Equations［J］.IEEE Transactions on Aerospace and Electronic Systems，1985，AES－21（1）：56－59.

［4］ KRAUSE L O.A Direct Solution to GPS－type Navigation Equations［J］.IEEE Transactions on Aerospace and Electronic Systems，1987，AES－23（2）：225－232.

［5］ ABEL J S，CHAFFEE J W.Existence and Uniqueness of GPS Solutions［J］.IEEE Transactions on Aerospace and Electronic Systems，1991，27（6）：952－956.

［6］ CHAFFEE J，ABEL J.On the Exact Solutions of Pseudorange Equations［J］.IEEE Transactions on Aerospace and Electronic Systems，1994，30（4）：1021－1030.

［7］ LEVA J L.An Alternative Closed－form Solution to the GPS Pseudo－range Equations［J］.IEEE Transactions on Aerospace and Electronic Systems，1996，32（4）：1430－1439.

［8］ KURAZUME R，HIROSE S，NAGATA S，et al.Study on Cooperative Positioning System（Basic Principle and Measurement Experiment）［C］／／Proceedings of 1996IEEE International Conference on Robotics and Automation.Minneapolis，MN：IEEE，1996：1421－1426.

［9］ PATWARI N，ASH J N，KYPEROUNTAS S，et al.Locating the Nodes：Cooperative Localization in Wireless Sensor Networks［J］.Signal Processing Magazine，2005，22（4）：54－69.

［10］ MOURIKIS A I，ROUMELIOTIS S I.Performance Analysis of Multirobot Cooperative Localization［J］.IEEE Transactions on Robotics，2006，22（4）：666－681.

［11］ PENNA F，CACERES M A，WYMEERSCH H.Cramér－Rao Bound for Hybrid GNSS－terrestrial Positioning［J］.Communications Letters，2010，14（11）：1005－1007.

［12］ MENSING C，SAND S，DAMMANN A.GNSS Positioning in Critical Scenarios：Hybrid Data Fusion with Communications Signals［C］／／Proceedings of 2009IEEE International Conference on Communications Workshops（ICC Workshops 2009）.Dresden，Germany：IEEE，2009：1－6.

［13］ TIAN Shi－wei，DAI Wei－heng，CHANG Jiang，et al.On the Agent Localizability of Hybrid GNSS－terrestrial Cooperative Positioning［C］／／第四届中国卫星导航学术年会论文集.武汉：Springer Berlin Heidelberg，2013：567－575.

［14］ QUEBE S，CAMPBELL J，DE VILBISS S，et al.Cooperative GPS Navigation［C］／／Proceedings of 2010IEEE／ION Position Location and Navigation Symposium（PLANS）.Indian Wells，CA：IEEE，2010：834－837.

［15］ GARELLO R，SAMSON J，SPIRITO M，et al.Peer－to－peer Cooperative Positioning［J］.Inside GNSS，2012（July／August）：56－65.