采用自回归滑动平均模型的地球自转参数短期预报

叶修松，何雨帆，曾 光，郭 海

（1.宇航动力学国家重点实验室，西安 710043；2.中国西安卫星测控中心，西安 710043）

1 引言

由于地球自转参数（Earth rotation parameters，ERP）的解算过程比较复杂，甚长基线干涉测量（very long baseline interferometry，VLBI）、卫星激光测距（satellite laser ranging，SLR）等高精度观测手段往往需要几天甚至更长的时间才能获取其变化值；全球定位系统（global positioning system，GPS）尽管解算速度较快（约3h），但GPS解算有较大的系统影响，长期稳定性不好，需要用VLBI和SLR解来进行修正［1］。因此，这些参数实际上是无法实时获得的。由于极移和日长的变化受众多激发源的影响，其变化不仅具有一定的线性趋势及多种周期变化趋势，同时还包括了复杂的不规则变化特性，这给预测工作带来了极大的困难。往往是预测几天之后，其预测误差便远远大于其观测误差。因此，对ERP的预测算法进行研究，建立更为合理、有效的预测模型，提高地球自转参数的预报精度，具有十分重要的意义［2－4］。

为此，本文拟采用自回归滑动平均模型（autoregressive moving average，ARMA）对ERP进行短期预报。该算法在于它不受地球自转动力学模型等因素的制约，具有计算速度快、算法稳定可靠等优点。

2 长自回归白噪化方法

ARMA（p，q）序列参数估计的较为有效且简便的方法是 “长自回归白噪化方法”。长自回归白噪化方法的基本思想是认为随机序列｛Xt｝ 可以用阶数较低的自回归模型拟合，拟合的残差作为白噪声的估计，再用最小二乘法的原理，估计出参数＝ （φ1，…，φp）和＝ （θ1，…，θp）。这一方法的特点是全部求解过程都是解线性方程组，避免了非线性运算。

长自回归白噪化方法的步骤为：

设有ARMA（p，q）序列 ｛Xt｝的一段样本X1，X2，…，XN。

（1）先用AR（pN）模型拟合一段样本，pN取适当的低阶，AR（pN）的参数是φ1，…，φpN。按照AR（p）序列参数的矩估计，由样本值X1，X2，…，XN，可以求出φ1，…，φpN的矩估计量，…，［5－7］。

（2）由于 AR（pN）模型为

将，…代入此式左端，就得到αt的估计值：

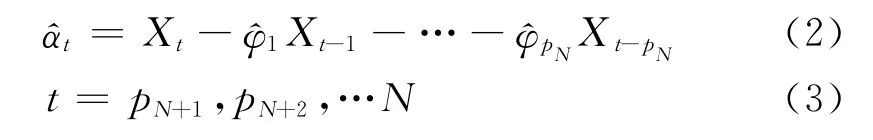
如果AR（pN）拟合的好，就应当是白噪声序列，如果拟合的不好，就不是白噪声序列。是否为白噪声序列，可以直接用 “周期图法”进行检验。如果不是白噪声序列，就要改变pN的值，直到｝ 为白噪声序列为止。

（3）对于 ARMA（p，q）序列：

有

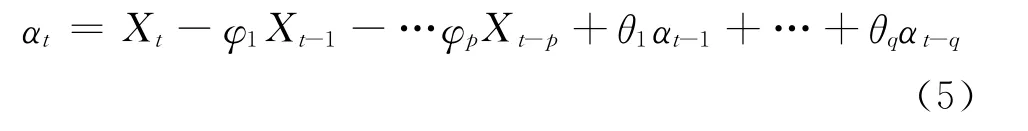
记

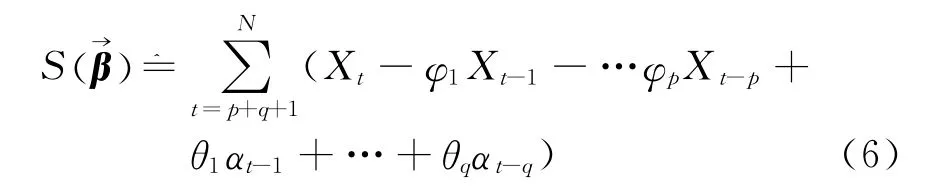
在S（）的表达式中，Xt，Xt－1，…，Xt－p是已知的样本值，αt－1，…，αt－q是由（4）式算得的αt的估计值，求和符号Σ的下标取为p＋q＋1是由于要计算出αt－q必需要求t≥p＋q＋1。

按最小二乘法的原理来确定未知参数φ1，…，φp，φ1，…，φp的估计值，…，，，…，。即要求

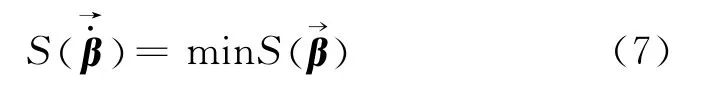
3 计算策略

3.1 日长变化的预报

日长（length of day，LOD）与 UT1－UTC是可以相互转换的，即扣除UT1－UTC的跳秒后，再作差分，结果的相反数即为LOD。UT1为世界时（universal time）、UTC为协调世界时（coordinated universal time）、TAI为原子时（international atomic time）、UT1R－TAI为从 UT1－TAI序列中减去潮汐分量的部分为，UT2R－TAI为从UT1RTAI序列中减去地球自转的周期性季节变化的部分。因此，对LOD的预报可以转换为对UT1－UTC的预报［1］。UT1－UTC的预报流程如图1所示［8］。

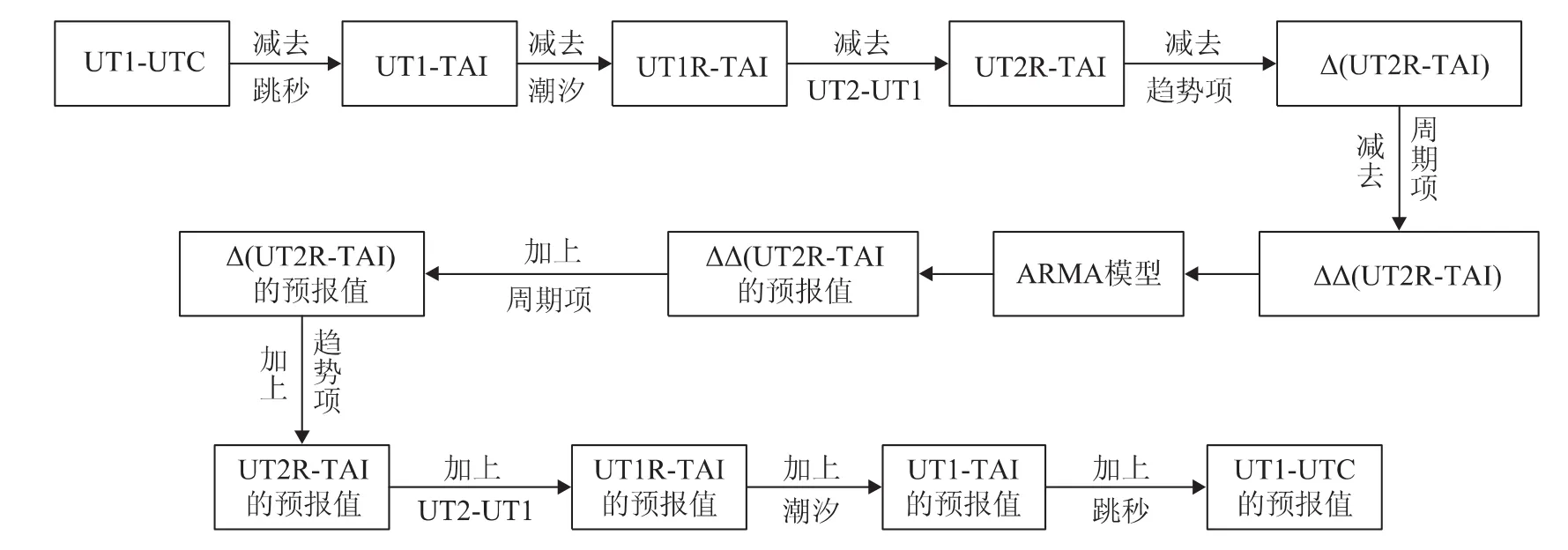
图1 日长变化预报的流程图

3.2 极移的预报

极移变化的预报算法如图2所示，包括建立预测模型和外推预测两个部分。在建立预测建模时，用最小二乘法计算出趋势项和周期项的拟合系数，计算公式为［9－10］

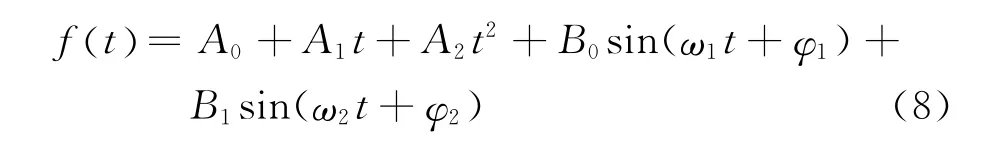
对于极移残差序列的预报也采用ARMA算法实现，极移序列ARMA预报的原理类同于日长变化的预报。

图2 极移序列预报的流程图

4 计算与分析

计算与分析的数据来源于地球自转服务（international Earth rotation service，IERS）官方网站公布的ERP时间序列。该序列包含1962－01－01至今的地球定向参数值，采样间隔为1d。实际计算选取6a极移时间作为基础序列长度，因为6a接近Chandler周期与周年的最小公倍数，这样更能体现地球自转参数的周期特征。采用ARMA模型要求时间序列必须为平稳的随机序列，通过上述的ERP计算策略分析发现，仅对ERP时间序列扣除周期项和趋势项之后所得的ERP残差子时间序列随机序列的波动性较明显、平稳性较差，而基于残差作二次差分后的子时间序列的波动更趋于平稳，更接近零均值。因此，本文基于自主编写的ERP短期预报软件分析了ERP残差子时间序列与残差作二次差分后的子时间序列对ARMA模型的适用性。

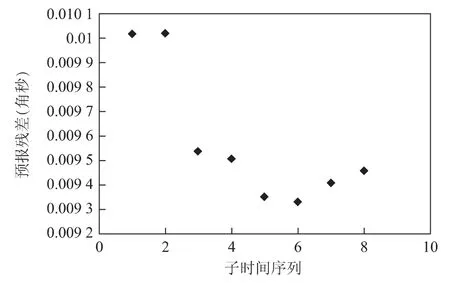
图3 PX残差序列预报7d的结果

图4 PX二次差分后残差序列预报7d的结果

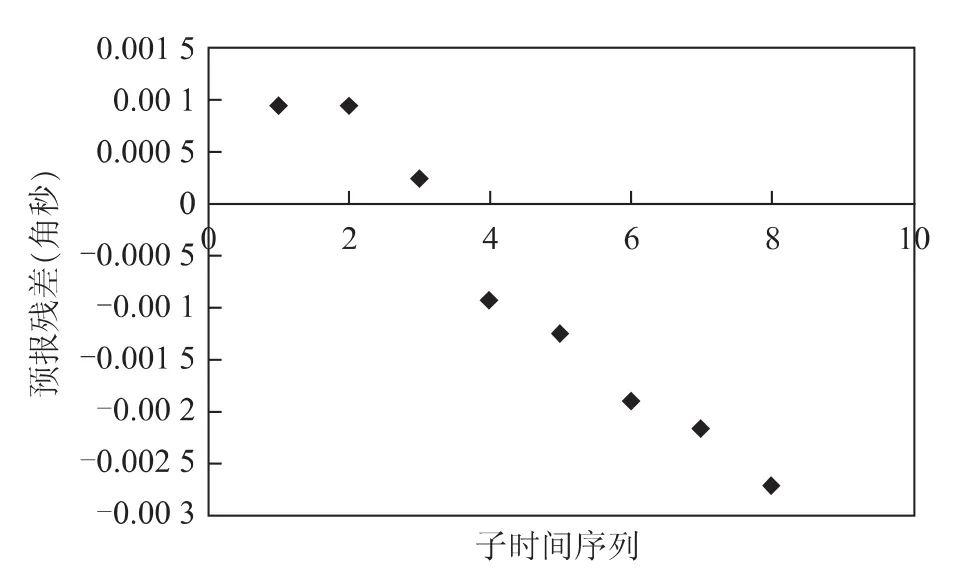
图5 PY残差序列预报7d的结果

图6 PY二次差分后残差序列预报7d的结果

图7 UT1－UTC残差序列预报7d的结果

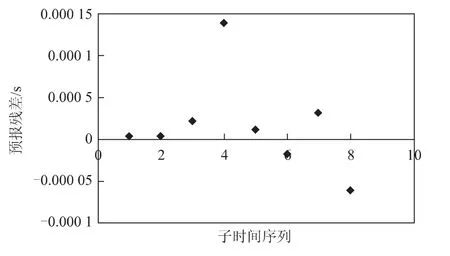
图8 UT1－UTC二次差分后残差序列预报7d的结果

从图3～图8可以得出，基于残差二次差分后的预报结果明显要优于直接使用残差预报的结果，其主要原因是剔除周期项和趋势项的残差（包括一次残差差分）序列没有明显的规律特征，其平稳性还不能满足平稳随机序列的条件。而基于残差二次差分后的残差子时间序列的波动更趋于平稳，更接近零均值。

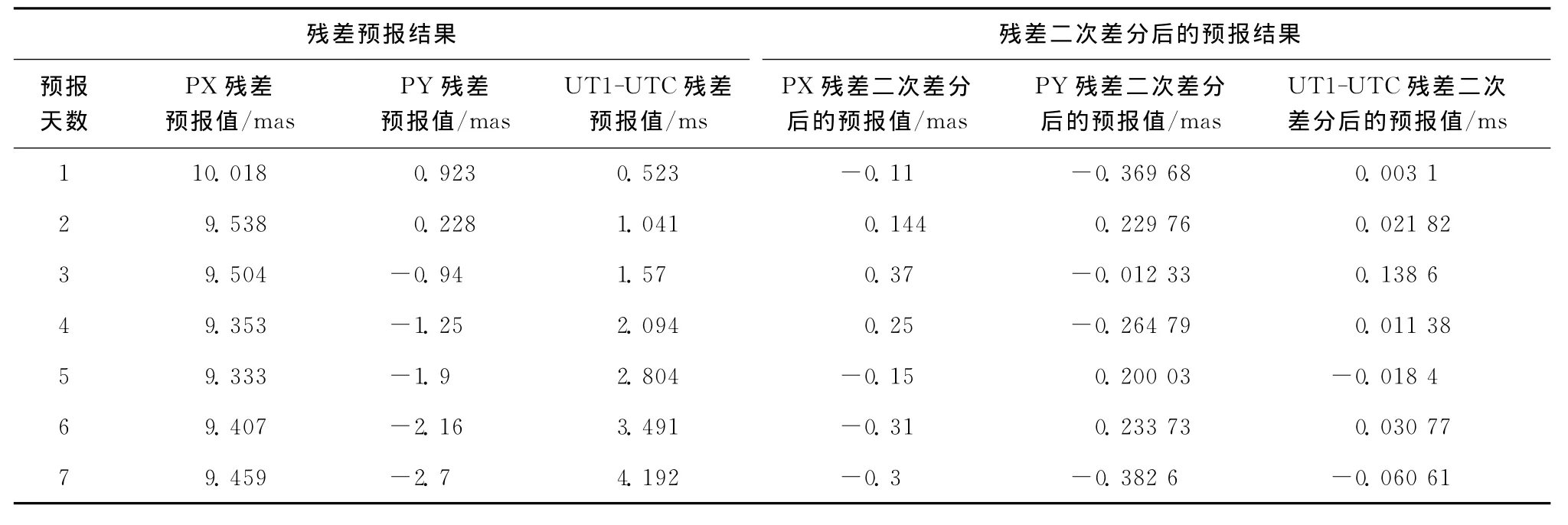
表1 基于ARMA算法的ERP 短期预报结果

从表1可知，直接采用残差时间序列预报1d的ERP精度约为：PX＝10mas，PY＝0.9mas，UT1－UTC＝0.5ms；采用残差残二次差分后的时间序列预报1d的ERP精度约为：PX＝0.1ms，PY＝0.4mas，UT1－UTC＝0.003ms。综上所述，本文采用的基于非线性自回归的ERP短期预报精度与IERS公布的结果相当。

5 结论与分析

本文采用线性自回归方法对地球自转参数进行短期预报，并与EOPPCC的结果进行比较，以验证预报模型的有效性。本文提出的基于ARMA的ERP短期预报技术已达到国际水平。本文还通过试验发现，基于ARMA方法进行ERP时间序列预报时，要求ERP时间序列不能过长或过短，其主要原因是数据精度不一致，从而影响预报精度。本文同时还验证了文献 ［2］提出的采用6a极移时间作为基础序列长度的有效性。另外，本文仅采用ERP时间序列本身来进行预报，没有考虑与之有极强相关性的大气角动量，这也是本文的不足之处。

［1］ ARTZ T，BERNHARD L，NOTHNAGEL A，et al.Methodology for the Combination of Sub－daily Earth Rotation from GPS and VLBI Observations［J］.Journal of Geodesy，2012，86（3）：221－239.

［2］ KOSEK W，MCCARTHY D D，LUZUM B J.Possible Improvement of Earth Orientation Forecast Using Auto－covariance Prediction Procedures［J］.Journal of Geodesy，1998，72（4）：189－199.

［3］ KOSEK W，KALARUS M，JOHNSON T J，et al.A Comparison of LOD and UT1－UTC Forecasts by Different Combined Prediction Techniques［J］.Artificial Satellites.2005，40（2）：119－125.

［4］ 徐君毅.基于截距修正的 GM（1，1）模型在极移实时预测中的应用［J］，大地测量与地球动力学，2010，30（1）：88－91.

［5］ 魏武雄，WILLIAM W S.时间序列分析—单变量和多变量方法［M］.易丹辉，刘超，贺学强，等，译.2版.北京：中国人民大学出版社，2009.

［6］ 潘国荣.基于时间序列分析的动态变形预测模型研究［J］.武汉大学学报：信息科学版，2005，30（6）：483－487.

［7］ 杨叔子.时间序列分析的工程应用［M］.2版.武汉：华中科技大学出版社，2007.

［8］ NIEDZIELSKI T，KOSEK W.Prediction of UT1－UTC，LOD and AAMχ3by Combination of Least－squares and Multivariate Stochastic Methods［J］.Journal of Geodesy.2008，82（2）：83－92.

［9］ THALLER D，KRÜGEL M，ROTHACHER M，et al.Combined Earth Orientation Parameters Based on Homogeneous and Continuous VLBI and GPS Data［J］.Journal of Geodesy.2007，81（6－8）：529－541.

［10］ CERVEIRA P J M.Earth Rotation Observed by Very Long Baseline Interferometry and Ring Laser［J］.Pure and Applied Geophysics，2009，166（8－9）：1499－1517.