理解教学价值 追求设计优化

【摘 要】教学立意源于对教学的价值判断，它取决于教师对教材的理解、对学生的理解和对教学的理解。教学价值是对“教什么”的定位选择，是对“为什么这样教”的概括诠释，是对“怎么教”的有力保障。为此，教学价值是教学设计的灵魂，理解和把握准数学的教学价值，就显得尤为重要。本文从“从问题到方程”这个课例，对教学价值的挖掘与选择进行研究与思考。

【关键词】教学价值 价值判断 教学预设 价值追思

一、课例背景分析及价值判断

苏科版《数学》教材七年级上册“第四章一元一次方程” “4.1从问题到方程”这节内容，为研究方程相关问题提供了一个的新视角，也是义务教育课程标准理念下教材编写的一个新突破。教材提供了下列三个教学素材。

素材一：怎样描述图中天平平衡所表示的数量之间的相等关系？

素材二：篮球联赛规则规定，胜一场得2分，负一场得1分，该篮球队赛了12场，共得20分。怎样描述其中数量之间的相等关系？

素材三：我国古代问题：以绳测井，若将绳三折测之，绳多4尺；若将绳四折测之，绳多1尺。绳长、井深各几何？

面对上述三个问题，首先需要思考的是提供的三个素材为什么要用方程来解决？用小学算术的方法不可以吗？弄清这个问题，学生才能认识“从问题到方程”中的“到”的价值，才能体现“从问题到方程”这节教学内容的本质诉求。那么，教材中提供的三个素材能够回答为什么要用方程来解决问题吗？如果不能回答，应该对教材作怎样的改造？这些问题要引起我们的关注和思考。

教材是采用“从天平到方程”导入新课的，这样的导入比较直观，学生容易接受。但是，对一个问题为什么不用学生已熟悉的算术方法去解，而要用方程方法去解揭示得不够。因此，在教学中必须增加环节，让学生明白用方程解决问题的来龙去脉。

本着这样的想法，我对教材提供的素材作如下改造：

可以选用“鸡兔同笼”问题作为研究问题的导入情境。第一，它是学生目前最为熟悉的情境之一。在小学里学生都接触，甚至还作为专题研究过；二是用它的“算术解法”（实是假设法）过渡到“方程解法”（也是假设法），既能显示从问题“到”方程的思维过程，更能凸显方程的本质，让学生清楚地知道，用方程去解决问题，第一步为什么要先设出未知数（设未知数主要是因为方程是“假设法”下的产物，“设”字实为“假设”之意）；三是此问题中的数量关系简明、简单，在学生现有的心智水平下，易用字母表示出来，从而容易将问题方程化，实现从问题“到”方程。

另一方面，改造教材中的问题模型。教材中提供的问题是零散的，得到的方程全是各不相同的，要想“通过从问题到方程，让学生初步感受方程是刻画现实世界相等关系的有效模型”，恐难奏效。为此，可以用“鸡兔同笼”中的方程为模型，以组织学生“秋游”为主题（上这节课时正值学校准备组织秋游活动），在“主题式”探究活动中，让学生初步感受方程是刻画现实世界相等关系的有效模型，更有实效性和教育性。

根据上述背景分析，本节内容的教学预设可按下列方式进行。

二、基于价值判断的教学预设

问题1 “鸡兔同笼，上有三十五个头，下有九十四只足，问鸡、兔各多少？”这是经典的古代名题，请同学们回忆一下，在小学里你是怎么解决这个问题的？

解答期盼： （1）“砍足法”。假设把兔子的足砍去一半， 则有３５×2=70（只）足，那么被砍去的足有94-70=24（只），故有24÷2=12（只）兔子。（2）“兔立法”。假设让兔子全“站立”起来，那么鸡、兔共有35×2=70（只）足，而实际多了94-70=24（只）足，故有24÷2=12（只）兔子。（3）“公平法”。兔有4只足，鸡有2只足，这样对鸡是否有些不公平？不过兔子没有翅膀，而鸡有2只翅膀，这样一想，也能算是公平了。则又可假设把鸡的两只翅膀也算足的话，那么就有35×4=140（只）足，这就说明鸡有46÷2=23（只），故原来有２３（只）鸡。

问题2 上述解决问题的方法主要运用的是小学数学知识，这几种方法有什么共同点？

解答期盼： 有些事情虽然没有发生，但我们可以在想象中假设它发生了，于是出现了合乎解决问题的情境，从而获得问题的答案。故上述解法，其实质就是“假设法”。

问题3 我们能否沿着假设法的思路，通过“用字母表示数”的方法来解决该问题呢？

解答期盼： （1）假设鸡有x只，则兔有（35-x）只。 根据鸡、兔共有94只足，就有2x+4（35-x）=94。余下的问题就变成学生熟知的问题了。（2）上面解答的思路是将小学阶段学习的“假设法”迁移到初中数学中，用方程来解决问题。

问题4 秋天是个收获的季节，学校准备组织部分同学去秋游。小明是秋游活动的负责人，你们能帮他解决下列问题吗？

请看题：学校组织七年级94名三好学生到玄武湖划船秋游，共用船35条，若每条大船可以坐4人，每条小船可以坐2人，如果小船有x条，那么可得方程 。

解答期盼： （1）将解决“鸡兔同笼”问题的经验延伸到“秋游划船”问题上来，再次经历根据未知数的意义列出方程的过程，体会用方程解决问题的思想方法。（2）反观列出的方程，产生“同一方程可表示不同问题背景”的意识，对“数学模型”有一种朦胧的感觉。

问题5 俗话说，兵马未动，粮草先行。现决定秋游活动自带水果，你能帮小明当好这个后勤部长吗？请看题：用94元钱买苹果和橘子共35斤，已知苹果4元每斤，橘子2元每斤。如果买了x斤橘子，那么可得方程 。

解答期盼： （1）对从问题到方程能有一个比较常态的转化。（2）初步形成“同一方程可表示不同的问题背景”的观念，对“方程是刻画现实世界数量相等关系的一种有效的数学模型”有一个初步的认识。

问题6 当秋游回来，小华向小明请教了四个问题，你们能帮小华解决吗？请看题：

（1）已知师傅每小时做4个零件，徒弟每小时做2个零件。现师、徒两人在35小时内完成94个零件的加工任务。那么徒弟做了多少小时（用方程表示）？

解答期盼： （1）对“从问题到方程”能有一个比较规范化的转化。即首先要确定未知数，并能用字母表示出来，然后根据已知数、未知数的意义列出方程。（2）进一步让学生体验“方程是刻画现实世界数量相等关系的一种有效的数学模型”的思想。即不同的问题背景，可用同一方程（数学模型）将之表示出来，再次加深对２x＋４（３５－x）＝９４理解，再次体验模型思想。

（2）在一次电脑知识竞赛中共有20道题。对于每道题，答对了得5分，答错了或不答的扣3分，邓民同学得了84分，则他答对多少道题（用方程表示）？

解答期盼： ①可以根据“答对的得分－答错或不答的扣分=84”，列出方程。设答对y道题，那么答错（２０－y）道题，则可得方程５y－３（２０－y）＝８４。②对模型化思想有进一步认识，让学生认识到不同的问题背景，可用不同的方程（数学模型）来表示。

（3）篮球联赛规则规定，胜一场得2分，负一场得1分，该篮球队赛了12场，共得20分。怎样描述其中数量之间的相等关系？

（4）我国古代问题：以绳测井，若将绳三折测之，绳多4尺；若将绳四折测之，绳多1尺。绳长、井深各几何？

解答期盼： 通过对上面（3）（4）二题的探究，期盼学生有下列之效：①根据本节课前面的思维活动积累下来的用方程解决问题的经验，对将实际问题转化成方程的数学建模技能有一个巩固提升的过程。②通过探究得到的9个方程，分析其“式结构”特征，为归纳一元一次方程的概念奠定基础。

问题7 现实生活中充满了大量的相等关系，方程的思想无处不在，现在就让我们再去感受一下方程的思想。

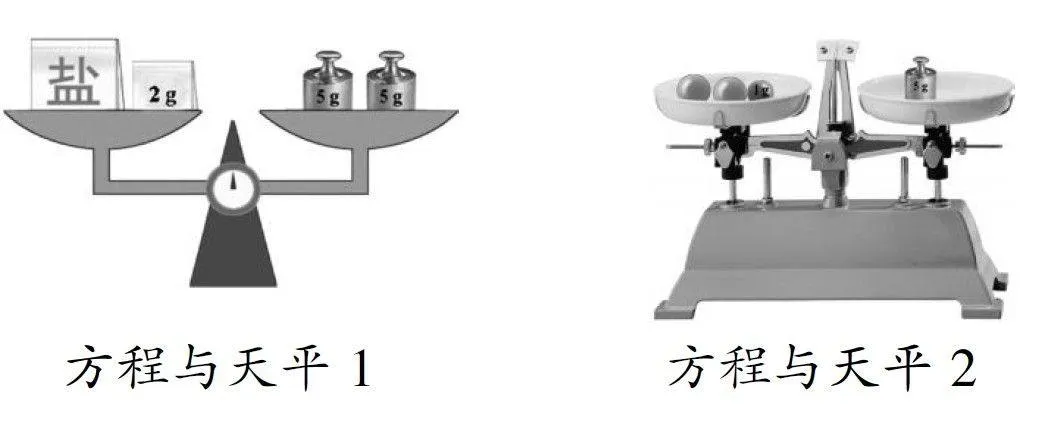
如图所示（方程与天平1），可以得到的方程为： x+2=10

如图所示天平（方程与天平2），可以得到什么样的方程？

解答期盼： 体会方程是解决实际问题中相等数量关系的有效模型，从天平的原理中，体会数学的应用价值，让学生快乐地学习数学。

三、课例设计中“到”的历程

本预设主要从下面三方面体现“到”的历程，凸显教学内容中的“到”的价值。

1．问题“到”方程。

通过探究“砍足法”“兔立法”“公平法”等解法，引导学生经历从小学算术（算法）到中学数学（方程）的探索历程，放大“到”的过程。这一过程也就是让学生清晰体会从“算术法”到“方程法”的过程，是一个“形异实同”的过程，是一个将新知识纳入到旧知识结构中去的过程。关键是本预设从旧知识出发，引导学生积极思维，有效参与，在合理继承“算术法”的内核（实为假设法）的前提下，又不失新意（提示了方程法的实质也为假设法），实现了从小学算术法向初中方程法的巧妙过渡，有力地激发了学生对数学的美好情感。

2．从方程“到”模型。

主题式探究是围绕某一中心问题展开“形散神不散”的探究活动。本预设，通过对“鸡兔同笼”问题的探究形成的基础，在以“秋游”为主题的系列问题探究中，凸显模型思想，挖掘“到”的价值。一是“同一个方程模型可表述不同的问题背景”，让学生感受方程的本质美；二是形成“不同的方程可以表述不同背景”的经验。

3.从模型“到”天平。

在研究了一些问题之后，将学生的视角从“方程”引入到“天平”，来感悟“方程与天平”的联系，那么学生对天平的认识，必然是不仅仅停留在小学那种简单的在“形”中“看”，而是在“数”中“思”，即由形象思维上升“到”理性思维，有力地落实了《数学课程标准》提出“螺旋上升”的要求。

四、对教学中“到”的价值的追思

1．从数学知识“到”学科智慧。

数学学科是一个让人聪明起来的学科，是一个让人增长智慧的学科。要体现上述思想，就教材教教材不行，就知识教知识也不行。必须要跳出教材教知识，跳出知识得经验，跳出经验长智慧。作为方程教学的首节内容教学要点，不是怎样教会学生将问题用“意会法”、“表格法”、“图象法”转化成方程的技能，而应让学生如何想“到”用方程的思想去解决问题，即不仅是知识层面和方法层面的教育，而应上升到智慧层面、素质层面的教育。好的数学教学活动，应突出数学的特点，揭示数学知识产生的自然性与合理性，要基于感性发展理性，让数学教学闪耀理性、智慧的光芒。

2．从课时目标“到”课程目标。

教学目标是教学活动的出发点与落脚点，这句话切中了把握教学目标的重要性。正因为如此，教师们才热衷于课时目标的分解与实现。在此理念下，“将数学分解成支离破碎的知识，过分关注知识的细枝末节，在非本质的形式上打转转、做文章，讲究立竿见影，还冠以学有用的数学、学实惠的数学”，这样在某种程度上讲是有可能利于学生掌握一些知识与技能，但也会让学生有只见树木不见森林，看不到隐藏在数学知识后面的数学本质、数学思想方法，导致课程目标难以实现。因此，在教学中不仅要注意将课程目标分解成课时目标，而且还要善于将课时目标反作用于课程目标，完成数学学科的教学任务。

3．从数学教学“到”数学育人。

数学学习在人的发展过程中有着不可替代的重要性和必要性。数学教育之根本意义在于培养求真理、讲道理、懂科学、有智慧、究根底、会思考的人。为此，数学教师要有“大数学学科思想”的胸怀与胆识，将数学教学上升到数学育人的层面上来开发教学资源。要把数学教学作为人类活动的数学来对待，用研究科学的方法来研究数学；要把数学教学作为理性思维的数学来对待，用理性思维思考数学；要把数学教学作为文化素养来对待，用数学素养来滋润学生的心灵。

【参考文献】

［１］卜以楼．凸显迁移能力的教学设计个案［J］．中国数学教育（初中），2009（11）

［２］卜以楼．要在“静”界中发展学生的思维能力［J］． 教学月刊·中学理科版，2012（4）

［３］教育部.义务教育数学课程标准（2011年版）［S］．北京：北京师范大学出版社，2012

［４］义务教育教科书·数学（七年级上册）［Ｔ］．南京：江苏科技出版社，2012