计算Lp 空间上Berezin变换范数的一种新方法＊

景彩霞，周立芳

（湖州师范学院 理学院，浙江 湖州313000）

0 引 言

设D是复平面上的开单位圆盘.符号dA＝（1／π）dxdy表示单位圆盘D上的正规化的Lebesgue测度，即A（D）＝1.Lp（D）（1≤p＜∞）是有所有满足

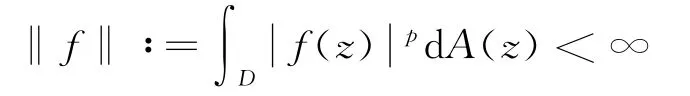
的函数f组成的Lebesgue空间.L∞（D）表示由所有的本性有界函数组成的空间，即对任意的f∈L∞（D）有：

Bergman空间（D）是由Lp（D）中所有的全纯函数组成的空间.可以看出，Bergman 空间（D）是Lp（D）的闭子空间.在（D）中，对任意的z∈D，在点z处的点赋值泛函是有界线性泛函.因此由Riesz引理知，对任意的f∈（D），存在函数Kz∈（D）满足

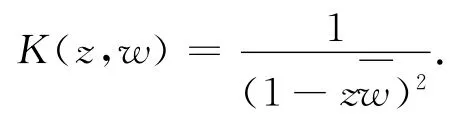
正规化的Bergman核kz为kz＝Kz／‖Kz‖2［1］.

对任意f∈L1（D），定义函数f的Berezin变换

Berezin变换是F.A.Berezin［2］在研究Kähler流形的量子化时首先引入的.后来Berezin变换在Bergman空间上的Toeplitz算子理论中发挥了重要作用［3～6］.

Berezin变换在Lp（D）上是有界的，当且仅当1＜p≤∞，这一事实很早就已经知道［5］.但是直到2008年，Dostanic才给出了其精确范数.在文献［7］中，Dostani证明了：

定理A 设1＜p≤∞，则有：

并且，当p＝∞时，等号右边的式子理解为1，其中‖B∶Lp（D）→Lp（D）‖ 表示Berezin变换B从空间Lp（D）映到Lp（D）上的算子范数.

本文主要以超几何函数的性质及Schur检验为工具，给出了上述定理的一个新的证明.这与Dostani在文献［7］中的方法是完全不同的.首先，我们介绍了超几何函数的性质及Schur检验等预备知识.其次，我们给出了定理A 的一种新的证明方法.

1 预备知识

本文将会用到超几何函数的知识.我们用传统符号2F1（α，β；γ，z）定义超几何函数

这里γ≠0，－1，－2，…，（α）0＝1，（α）k＝α（α＋1）…（α＋k－1）.其中：k≥1.

为方便参考，我们列出几个超几何函数的相关公式［8］：

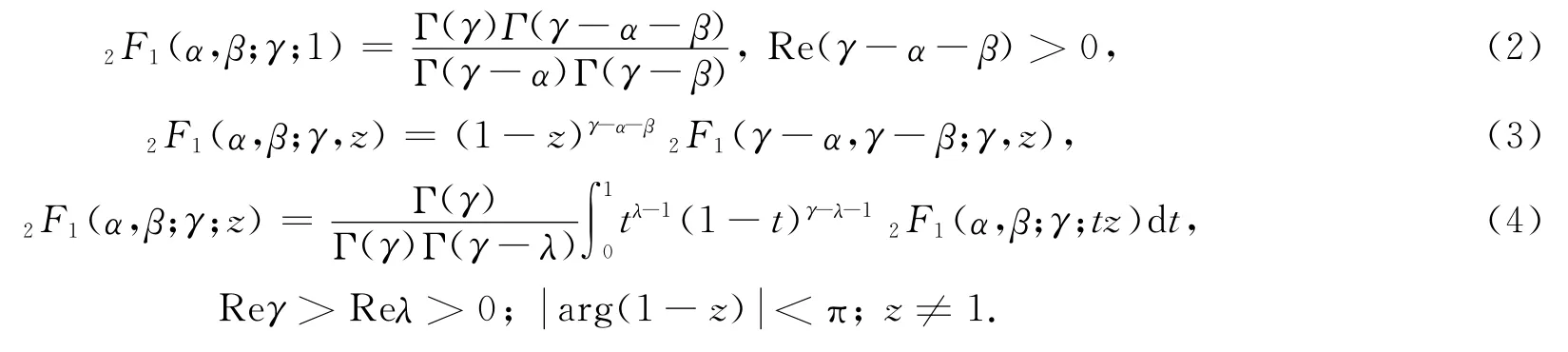
引理1 若Reδ＞0，且Re（λ＋δ－α－β）＞0，则有：

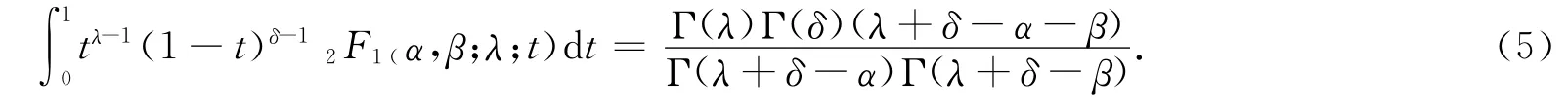
证明 注意到，公式（5）左右两边在z＝1连续的，令z→1，两边取极限，再利用（2）即得此引理.

下面的引理可由文献［9］中的定理1.4.10直接得到.

引理2 设α是一实数，γ＞－1，则有：

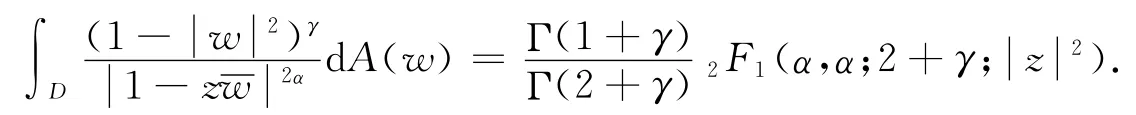
下面的结果通常被称作Schur检验，它是一种证明积分算子的Lp－有界性非常有效的工具［1］.

引理3 假设（X，μ）是一个σ－有限测度空间.K（x，y）是一个定义在X×X上的非负可测函数，T是与其相关的积分算子，定义为：

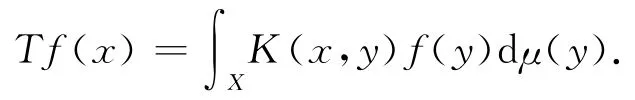
若1＜p＜∞且，如果存在一个正常数C和一个X上的正可测函数u满足，对于X上的几乎每一个x都成立：

并且，对于X上的几乎每一个y都成立：

那么，T在Lp（X，μ）是有界的，并且.

2 定理A 证明的新方法

证明 我们首先证明p＝∞的情形.由于

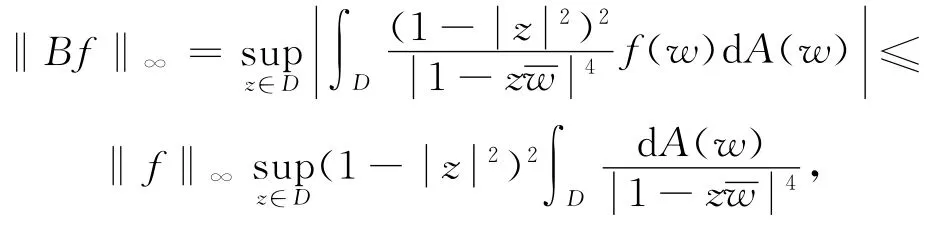
所以

由引理2和公式（3），我们发现

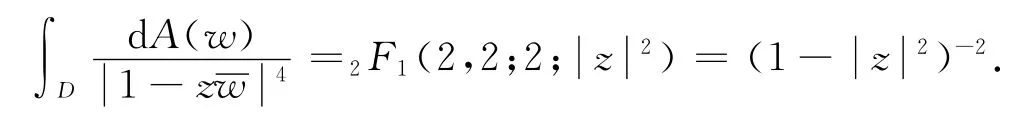
因此

证明反向不等式，考虑固定函数f＝1.容易得到：

下面证明1＜p＜∞的情形.我们运用Schur检验（引理3）.令

其中q是p的共轭指标.只需证明，对于每一个z∈D都成立：

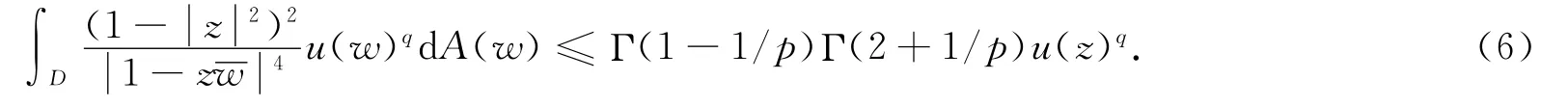
且对于每一个w∈D都成立：

我们只需证不等式（6），不等式（7）类似可证得.由引理2和公式（3），我们有：

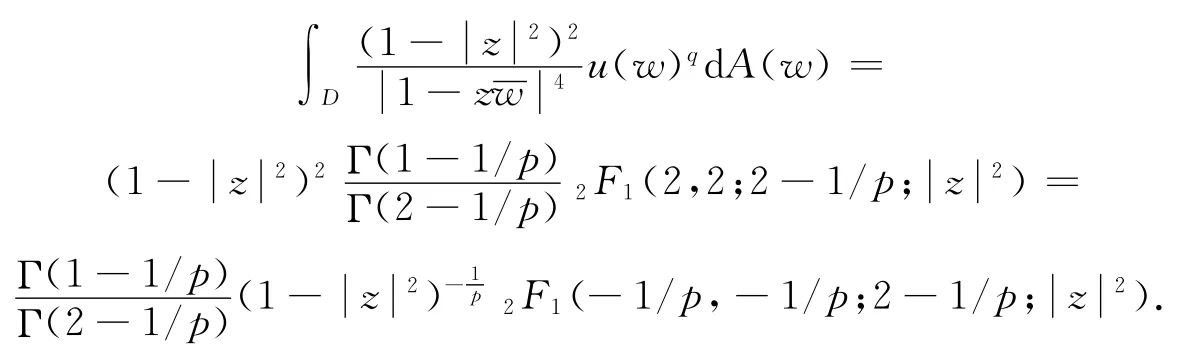
注意到，上面的超几何函数的Taylor展开式中的系数都是正的，所以它在区间［0，1）上是单调递增的，利用公式（2），有：

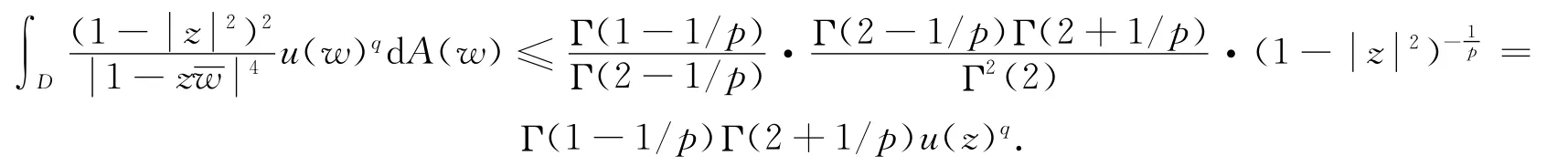
这就证明了公式（6）.这样得到：

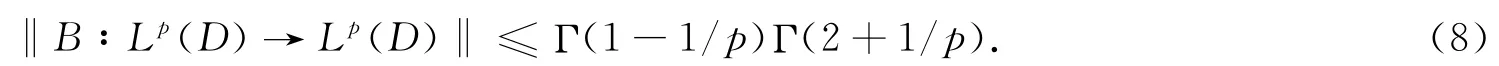
下面我们证明反向的不等式：

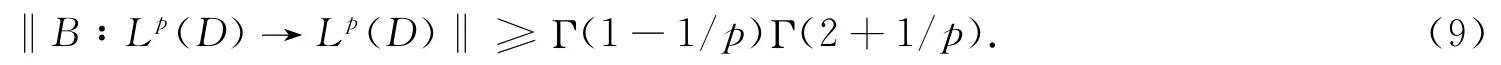
对任意给定ε＞0 定义

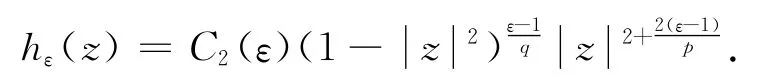
其中：

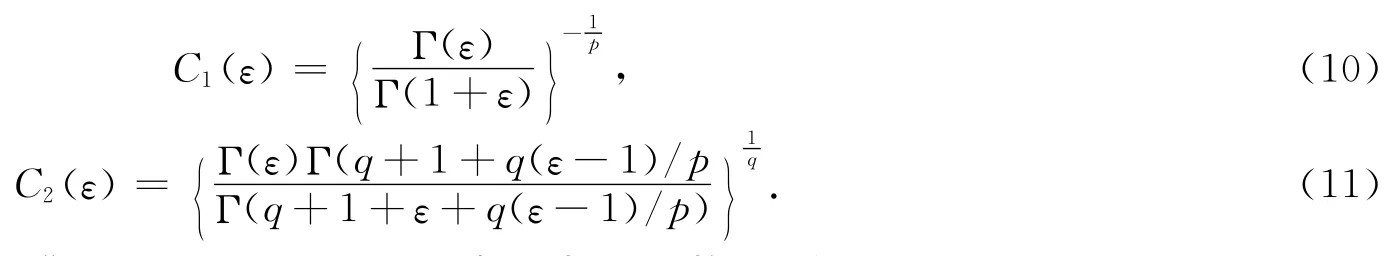
通过简单计算知‖gε‖p＝‖hε‖q＝1.利用引理2和极坐标系代换，我们得到：

最后一步等式由公式（5）得到.注意到

这说明

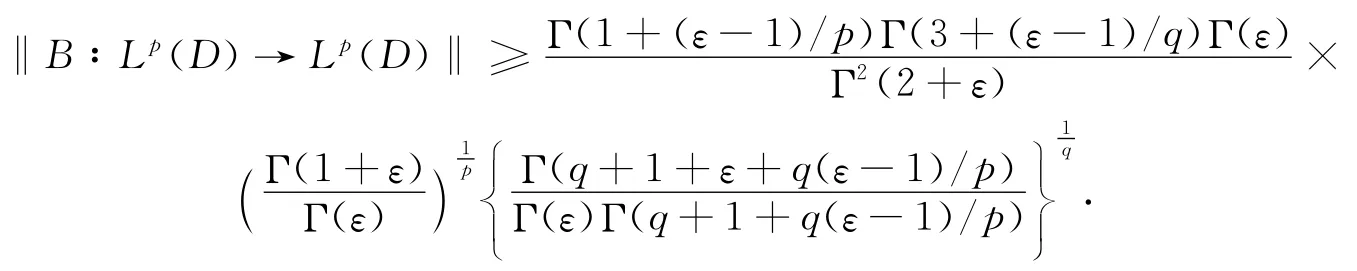
对上面的不等式两边通过ε→0＋，两边取极限即得（9）.

因此，由式（8）、式（9）知，当1＜p＜∞时，

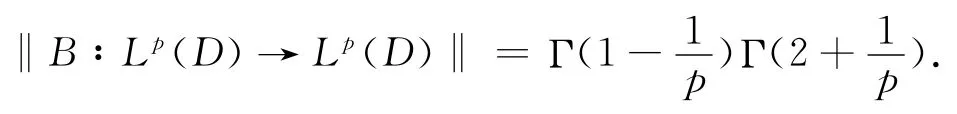
然后，使用Γ（x＋1）＝xΓ（x），结合余元公式

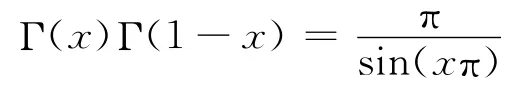
即得.定理A 证毕.

［1］Zhu K.Operator Theory in Function Spaces［M］.Providence：2nd ed，Amer Math Soc，2007：76－77.

［2］Berezin F A.Quantization［J］.Math USSR Izvestiya，1974（8）：1109－1163.

［3］Ahern P.On the Range of the Berezin Transform［J］.J Funct Anal，2004（215）：206－216.

［4］Ahern P，Cuckovic Z.A theorem of Brown－Halmos Type for Bergman Space Toeplitz Operators［J］.J Funct Anal，2001（187）：200－210.

［5］Hedenmalm H，Korenblum B，Zhu K.Theory of Bergman Spaces［M］.New York：Springer，2000：28－51.

［6］Korenblum B，Zhu K.An Application of Tauberian Theorems to Toeplitz Operators［J］.J Operator Theory，1995（33）：353－361.

［8］Erdélyi A，Magnus W，Oberhettinger F，et al.Higher Transcendental Function（Vol I）［M］.New York：McGraw－Hill，1953：392－399.

［9］Rudin W.Fuction Theory in The Unit Ball of［M］.New York：Springer－Verlag，1980：19.