基于非等间隔GM（1，1）模型的固体电枢初速预测

张 祎，杨春霞，李贞晓，栗保明

（南京理工大学 瞬态物理国家重点实验室，南京210094）

固体电枢初速的一致性和稳定性是衡量电磁轨道炮发射性能的重要指标之一。随着发射次数的增加，发射环境（如轨道磨损、电枢转捩、身管形变等）向着不利于电枢初速保持一致和稳定的方向发展。固体电枢电磁轨道炮发射系统复杂，影响发射的因素很多，而且在发射过程中因素之间相互影响作用，作用关系不明确；发射过程受到强电磁场的作用，只能借助间接的方法获取特征参数，因此所得到的信息是不完全的。而灰色理论[1]恰恰能解决“贫信息”、“少数据”情况下系统性能分析的不足。其中GM（1，1）模型在预测中的应用是最为广泛的，在不同的领域中研究者们先后对模型进行了改进[2－7]，在不同程度上提高了预测精度。

在固体电枢初速影响因素分析的基础上，本文采用原始数据光滑变换和背景值的积分变换组合的方法对经典非等间隔离散GM（1，1）预测模型进行了改进，在只调整固体电枢外直径的条件下，对小口径固体电枢电磁轨道炮连续发射实验进行了拟合和预测，并据此对固体电枢初速一致性进行了分析。

1 电磁轨道炮固体电枢初速主要影响因素分析

美军研究表明弹丸速度达到2～3km/s就可以满足现代常规战争的需求，在这样的速度范围内，固体电枢比等离子体电枢具有更高的能量效率和更好的作用性能，因此一直以来都是工程研究的重点，其中C型电枢是电磁轨道炮常用的固体电枢结构形式[8]。随着弹丸设计、轨道设计和发射连续性问题的解决，固体电枢电磁轨道发射技术的工程化应用研究正在如火如荼地进行，而发射装置的稳定性和固体电枢初速的精度就成为当前研究的重点。

影响固体电枢发射精度的原因主要有：转捩、几何误差、热误差、载荷误差、振动误差、刚度误差等，因果关系如图1所示。

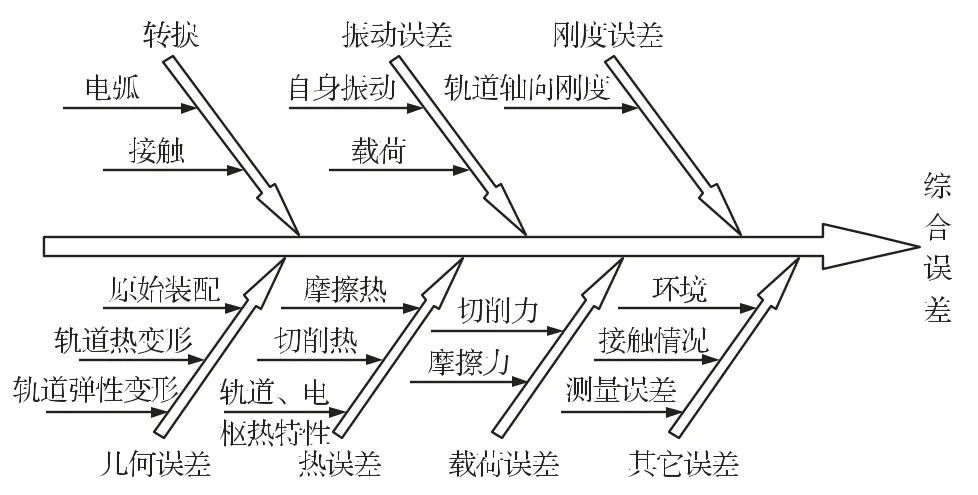
图1 电磁轨道炮误差源因果图

国内外公开发表的文献主要针对固体电枢电磁轨道发射过程中出现的个别问题（如电枢转捩、轨道刨削、速度趋肤效应、焦耳热、接触电阻等），开展针对性的理论研究、仿真分析和实验测量。笔者利用灰熵关联法[9]和灰色模型研究了电磁轨道发射中各因素的随机波动对发射系统的影响，但是发射过程十分复杂而且影响因素众多，因此在电磁轨道发射实验过程中，需要对影响精度和稳定性的因素的作用进行系统分析和研究。由于固体电枢过盈量对电枢初速的影响非常大，因此本文将进一步研究过盈量对电枢初速一致性的影响。

2 固体电枢初速一致性分析

2.1 非等间隔离散GM（1，1）模型的改进

由于发射系统具有很强“灰色”，因此下面将利用灰色理论中的预测能力对固体电枢初速的一致性进行分析。由于电磁轨道炮的发射过程是离散的，且每次的发射使用的电枢是不完全一致的，因此使用非等间隔离散GM（1，1）模型对固体电枢实测发射速度进行预测。

本文在经典离散非等间隔 GM（1，1）模型[2]的基础上进行了如下改进：

①原始序列光滑处理。原始数据的光滑特性是影响灰色模型预测精度的重要因素之一[10]。为了使振荡序列更为光滑，采用对数－幂函数数据变换方法[6]：

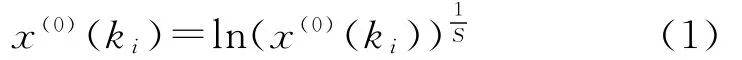
式中：x（0）（ki）为非等间距原始数据序列的第ki个数值，间距Δki＝ki－ki－1≠const，i＝1，2，…，n，幂指数S∈[0.7，1）。

②背景值处理。模型中的背景值是t轴上[ki－1，ki]区间内曲线x（1）（t）与t轴所围的面积。传统的背景值z（1）（ki）为图1中的梯形面积，其构造公式 为：，其中，x（1）（ki）为非等间距x（0）（ki）的一次累加生成序列，这与实际x（1）（t）与t轴所围面积误差较大，误差为图2中的阴影部分，因此采用积分形式重构背景值[4]。

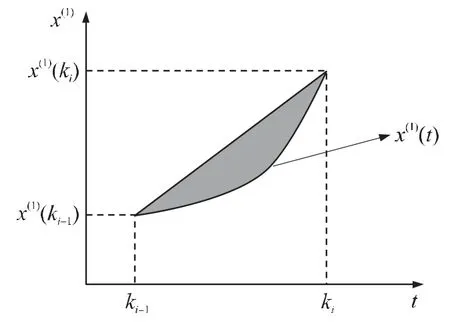
图2 传统背景值误差源

背景值的计算公式[11]为

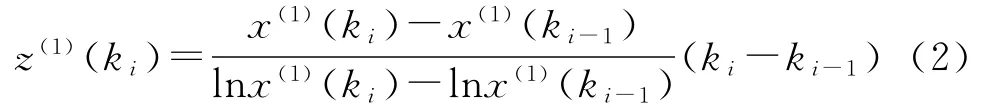
下面将根据改进的非等间隔灰色预测模型进行小口径电磁轨道炮发射实验固体电枢初速的预测。

2.2 小口径固体电枢电磁轨道炮初速预测

以20mm口径固体电枢增强型双轨坡膛式电磁轨道炮为实验对象，放电模块为6个，模块电感40μH，电容1 200μF，充电电压8kV，电枢质量6.24g。在实验过程中保持所有参数不变，固体电枢的直径的制造范围为（20.0±0.06）mm，实验测试结果见表1，其中，d（0）为电枢直径，v（0）为电枢实测初速。

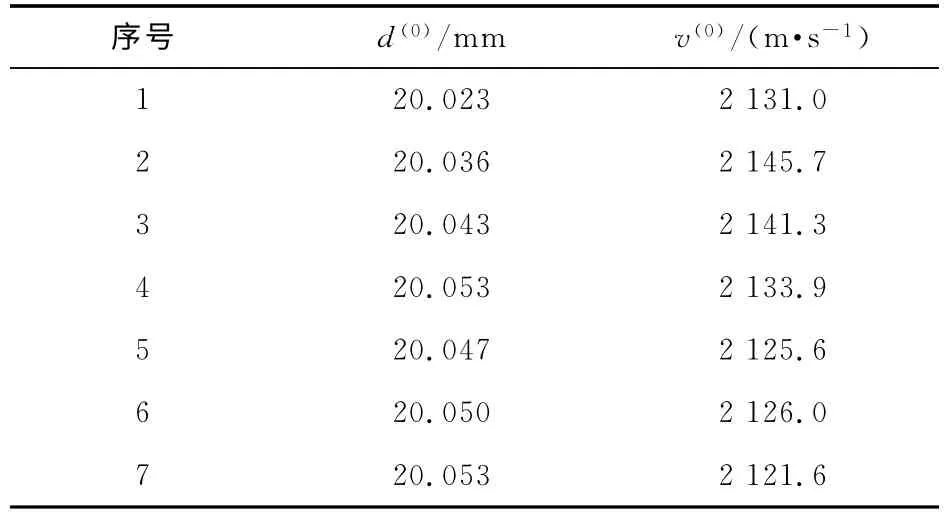
表1 实验测试结果

将表1中1～5次的数据作为建模样本建立非等间隔GM（1，1）模型。首先对原始数据序列进行对数－幂函数变换和归一化处理，数据变换后列于表2，其中，d（1），v（1）分别为归一化处理后的电枢直径和电枢实测初速。

表2 数据预处理结果

得到v（1）（ki）的估计值（ki）为

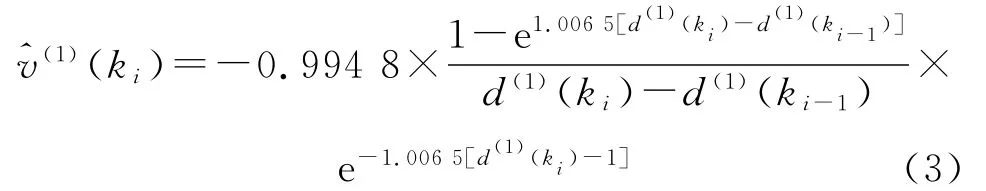
将（ki）还原后，电枢实测初速v（0）、拟合速度（0）及两者相对误差e见表3。

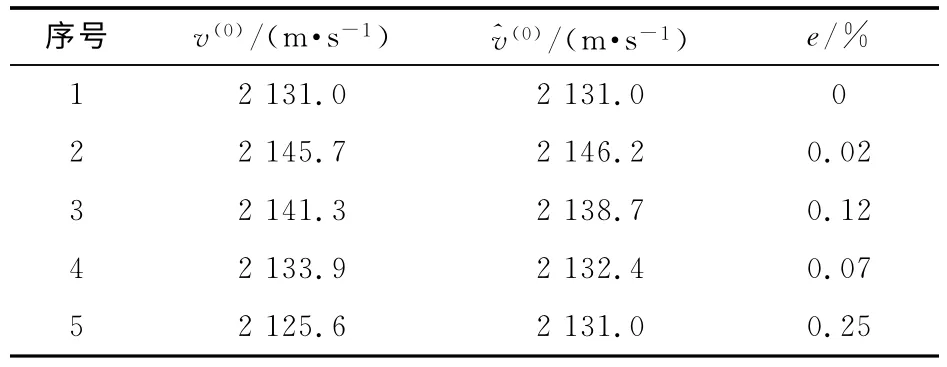
表3 非等间隔GM（1，1）模型拟合速度与相对误差

采用关联度R、后验差C和小误差概率P对模型的精度进行检验，检验标准参见文献[1]。本文中所建的非等间隔GM（1，1）模型的精度计算结果为：C＝0.265 6，P＝1，R＝0.668 5，拟合值最大相对误差小于0.3%，因此该模型拟合精度较高，可用于所研究发射系统固体电枢速度的预测。

对表1中第6、第7次的发射进行预测，结果见表4。

表4 非等间隔GM（1，1）模型预测速度与相对误差

从预测结果和测得速度的相对误差可以看出该模型的预测精度较高，达到99.6%。

2.3 结果分析

由表3和表4，得到速度实测值与拟合值以及用改进的非等间隔离散GM（1，1）模型预测的电枢速度对比曲线，如图3所示。

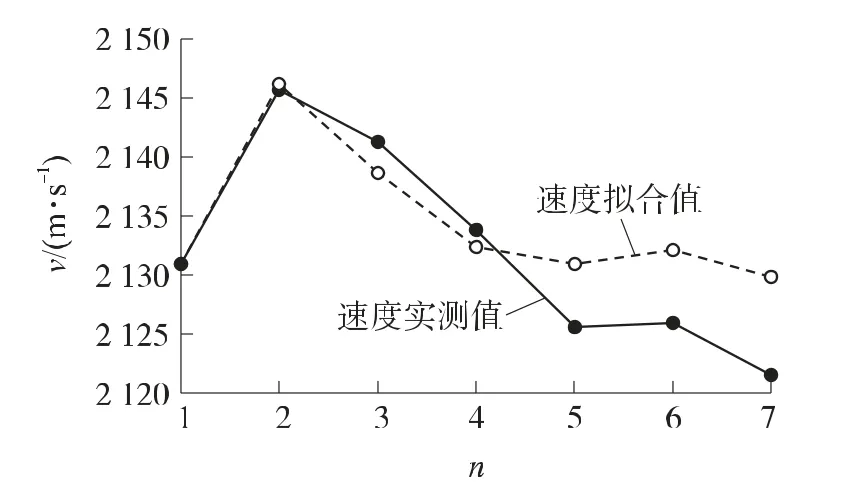
图3 速度实测值与拟合值、预测值对比图

从图3曲线分布可以看出非等间隔GM（1，1）模型计算的结果和实测结果趋势一致，只是曲线的变化趋势较为平缓，尤其是在预测阶段。

从式（3）可以看出，系统发展系数为1.006 5，这说明固体电枢直径对速度的发展是起促进作用的。假设在第7发之后固体电枢直径取作｛20.052，20.048，20.05，20.054，20.056｝，根据本文所建模型得到预测的电枢速度值为｛2 129.7，2 128.7，2 129.5，2 129.5，2 127.6｝。图4给出了电枢直径与初速预测数据分布曲线。

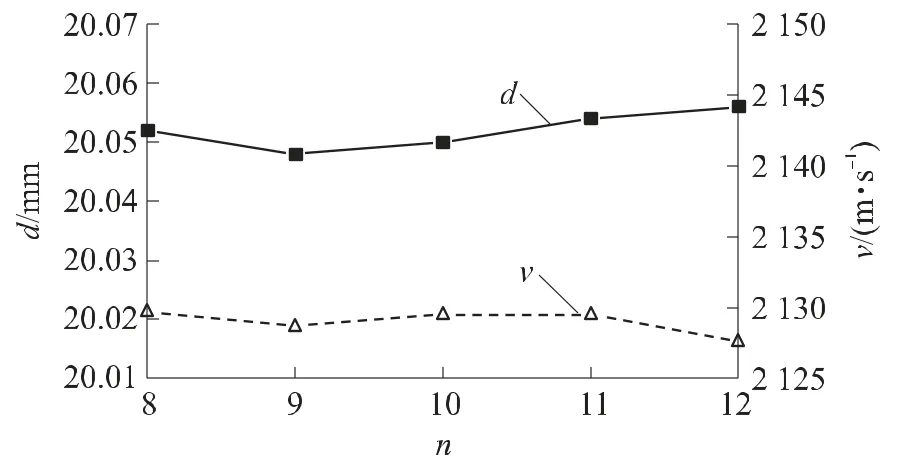
图4 电枢直径与初速预测数据分布曲线

从图4可以看出，在不改变其它参数的条件下，增加电枢直径意味着电枢和轨道间的接触电阻减小，这对于提高发射稳定性和一致性是非常有利的；但是随着发射次数的增加，仅仅改变电枢直径将不能弥补发射环境恶化带来的负面影响，需要整体调整结构参数，例如增加电枢质量、提高充电电压等，而这一系列的改进措施都可以借助预测模型进行时间点的确定，但此项工作需要发射实验的配合，在接下来的研究中将继续深化此项工作。

3 结论

针对固体电枢电磁轨道炮发射的一致性和稳定性问题，本文以小口径发射系统为研究对象，研究了固体电枢直径变化对初速一致性的影响。通过对灰色预测模型现有改进方法的总结和组合，本文采用原始数据光滑处理和背景值积分构造相结合的方法对离散非等间隔GM（1，1）灰色预测模型进行了改进，并利用该模型对（20.0±0.06）mm直径范围内的电枢速度进行了拟合和预测，精度均达到99.6%以上；利用所建模型获得了今后实验时电枢直径的变化规律，根据该变化规律可以实时调整参数的匹配方案，这在一定程度上有助于提高发射的稳定性。该方法的应用为解决固体电枢电磁轨道炮发射实验中电枢直径随机变化对电枢速度的影响提供了一种有效的预测分析方法。

在目前固体电枢电磁轨道炮发射研究中，由于影响电枢初速的因素繁多且作用关系不能用准确的数学表达式进行描述，因此利用灰色预测模型研究实验参数对电枢初速的影响，作为一种新的研究方法对电磁轨道发射机理的了解是有现实意义的。

[1]邓聚龙.灰色理论基础[M].武汉：华中科技大学出版社，2008.DENG Ju－long.The basis of grey system theory[M].Wuhan：Hua Zhong Sci ＆ Tech Press，2008.（in Chinese）

[2]刘思峰，郭天榜，党耀国.灰色系统理论及其应用[M].北京：科学出版社，2009.LIU Si－feng，GUO Tian－bang，DANG Yao－guo.Grey system theory and application[M].Beijing：Science Press，2009.（in Chinese）

[3]王钟羡，吴春笃，史雪荣.非等间距序列的灰色模型[J].数学的实践与认识，2003，33（10）：16－20.WANG Zhong－xian，WU Chun－du，SHI Xue－rong.A gray mold for non－equidistant sequence[J].Mathematics in Practice and Theory，2003，33（10）：16－20.（in Chinese）

[4]戴文战，李俊峰.非等间距 GM（1，1）模型建模研究[J].系统工程理论与实践，2005，9（9）：89－93.DAI Wen－zhan，LI Jun－feng.Modeling research on non－equidistance GM（1，1）model[J].Systems Engineering Theory ＆Practice，2005，9（9）：89－93.（in Chinese）

[5]李翠凤，戴文战.非等间距GM（1，1）模型背景值构造方法及应用[J].清华大学学报（自然科学版），2007，47（S2）：1 729－1 732.LI Cui－feng，DAI Wen－zhan.Determinator of the background level in the non－equidistant GM（1，1）model[J].Journal of Tsinghua Univ（Sci ＆ Tech），2007，47（S2）：1 729－1 732.（in Chinese）

[6]李小力，李言俊，张科.改进的灰色预测模型在导弹中的应用[J].计算机仿真，2010，27（8）：33－36，60.LI Xiao－li，LI Yan－jun，ZHANG Ke.Improved grey forecasting model of fault prediction in missle applications[J].Computer Simulation，2010，27（8）：33－36，60.（in Chinese）

[7]王正新，党耀国，裴玲玲.基于GM（1，1）幂模型的振荡序列建模方法[J].系统工程与电子技术，2011，33（11）：2 440－2 444.WANG Zheng－xin，DANG Yao－guo，PEI Ling－ling.Modeling approach for oscillatory sequences based on GM（1，1）power model[J].Systems Engineering and Electronics，2011，33（11）：2 440－2 444.（in Chinese）

[8]RIP L，SATAPATHY S，HSIEH K T.Effect of geometry change on the current density distribution in C－shaped armatures[J].IEEE Transaction on Magnetics，2003，39（1）：72－75.

[9]张祎，杨春霞，栗保明.基于灰熵分析法的电枢出口速度影响因素分析[J].弹道学报，2011，23（1）：93－96.ZHANG Yi，YANG Chun－xia，LI Bao－ming.Analysis on factors influencing muzzle velocity of armature based on grey relation entropy method[J].Journal of Ballistics，2011，23（1）：93－96.（in Chinese）

[10]徐进军，王海成，白中杰.灰色预测模型若干改进方法[J].测绘信息与工程，2011，36（4）：1－3，25.XU Jin－jun，WANG Hai－cheng，BAI Zhong－jie.Improvement of grey prediction model[J].Journal of Geomatics，2011，36（4）：1－3，25.（in Chinese）

[11]何庆飞，陈桂明，陈小虎，等.基于改进灰色预测模型的液压泵寿命预测[J].润滑与密封，2011，36（7）：27－31，35.HE Qing－fei，CHEN Gui－ming，CHEN Xiao－hu，et al.Life prediction of hydraulic pump based on the improved grey forecasting model[J].Lubrication Engineering，2011，36（7）：27－31，35.（in Chinese）