空间飞行器的一种直接定点入轨控制方法

刘新建，郝子龙，高兴龙

（国防科学技术大学 航天科学与工程学院，长沙410073）

直接定点入轨是要求火箭克服各种干扰，直接将飞行器一次性送入给定的轨道，且关机时刻的6个轨道要素应与预定入轨点的6个轨道要素相等，或者距离和速度偏差为任务要求允许。直接定点入轨控制对于一些空间快速响应任务如空间应急救援、空间快轨运输等具有特别的意义，有助于实现与目标飞行器的远程直接交会，克服以往两飞行器在轨道间小推力多脉冲调相变轨交会持续时间很长的缺点。由于基础级采用摄动制导控制以及发动机后效应的影响，基础级的入轨误差与标准轨道相差较大，严重影响与基础级分离后的飞行器定点入轨，因此，需要研究定点入轨控制方法。

过去火箭入轨控制方法通常是两类：一类是火箭基于标准轨道的摄动制导，利用小偏差理论对轨道进行摄动误差校正，显然不能适应大偏差干扰的控制；另一类方法是不依赖标准轨道只与边界条件相关的显式迭代制导或自适应制导方法，在适应纵向初始大偏差的控制精度方面较摄动制导方法有了较大改进，这其中的典型代表是美国Saturn－5号运载火箭IMG（Iterative Missile Guidance）制导方法[1－2]和航天飞机LTG（Linear Tangent Guidance）线性正切制导律方法[3－4]，这些方法应用时，侧向通道通常限制为小偏航角，小于10°；其次，这些方法对纵向偏差的自适应控制只控制了轨道根数如长半轴、偏心率、轨道倾角、升交点赤经，而对入轨相位是放开的，即入轨位置没有约束，无法实现一次性直接定点入轨控制。

近来，Lu Ping[5]，Calise A J[6]，Gath[7]对航天飞机在大气层内飞行段火箭推力和气动力组合的定点入轨约束控制进行了研究，但没有研究火箭在大气层外推力大小不可调的定点入轨控制。近期国内关于火箭自适应迭代控制的研究如茹家欣、陈新民、李华滨等[8－10]，均没有涉及直接定点入轨控制的情况。

1 直接定点入轨控制策略和方法

初始偏差对滑行后定点入轨精度干扰较大，为抑制其影响实现直接定点入轨，需要包括实时弹道规划与闭路控制2个阶段，流程如图1所示。

图1 直接定点入轨控制流程图

1.1 点火控制策略

传统空间飞行器末级点火策略通常是按设计的标准轨道点火时刻点火，即使在只有纵向初始偏差干扰的情况下，由于火箭推力大小不可调，按照标准点火时刻，入轨相位就不得不放开，从而产生与初始偏差干扰对应的入轨误差，该误差少则几十km，多则几百km。为此，如图1所示，应采取实时点火控制策略，根据导航测量计算给出的初始状态，实时规划点火时刻及其点火姿态角参数，以满足定点入轨的边界条件。因为增加了点火时刻变量，改变了点火状态，从而克服了推力不可调的矛盾。这种点火控制规划需要与动力段虚拟闭路控制一体化求解，这种虚拟闭路控制方法只参与弹道规划，而虚拟控制算法与变轨时的闭路控制算法完全相同。当存在侧向初始大偏差干扰时，需要采用与下述第2节提出的非线性鲁棒自适应控制方法结合，以匹配弹道规划与闭路控制，有效抑制纵向和侧向的较大初始偏差干扰，达到一次性直接定点入轨控制目标。

1.2 鲁棒自适应闭路控制策略

火箭一旦点火后，就按照如下鲁棒自适应控制策略和方法进行闭路控制直到关机。

设φ，ψ分别为箭体在发射惯性系中的俯仰、偏航姿态角；F为发动机的轴向推力；gx，gy，gz为地球引力加速度分量；m0，分别为火箭的初始质量和燃料质量流量。火箭在发射惯性系真空段的运动微分方程为

从运动方程可以看出，纵向运动的俯仰角φ不影响侧向Z分量的运动，即侧向运动只受偏航角的控制；但侧向运动影响纵向平面内的运动控制，偏航角越大，耦合影响越强烈。这是一种单向耦合，于是构造变轨段的鲁棒自适应闭路控制算法，大致概括如下：

①滑翔结束后，利用IMG侧向通道控制律，由初始偏差和侧向边界条件计算偏航角，幅值与初始偏差有关，偏航角的幅值在滑行段的弹道规划中与点火时间、点火姿态角一样，是规划变量。

②补偿修正大偏航角对俯仰通道的耦合影响，以确保闭路非线性迭代稳定性。

③改造LTG控制算法，求得满足纵向边界的俯仰角指令。

④判断前后制导周期内的俯仰角指令值之差，如果大于设定阈值就结束迭代，转入常值俯仰角飞行；否则重复上述过程，先偏航后俯仰，循环往复迭代直到按长半轴关机。

点火时间、点火姿态角和偏航角幅值是实时弹道规划得出的，以抑制初始偏差对入轨位置的干扰；点火后进行变轨段直接入轨的闭路控制，主要抑制火箭推力变化和姿态控制偏差等干扰的影响。

侧向通道偏航角指令计算利用Saturn－5的侧向计算方法[11]，下面仅对纵向通道控制算法的改造进行简要概括说明，详见作者文献[12]。

2 航天飞机控制律及算法改造

一旦点火后，纵平面内飞行器推力方向单位向量u采用航天飞机LTG控制律[4]：

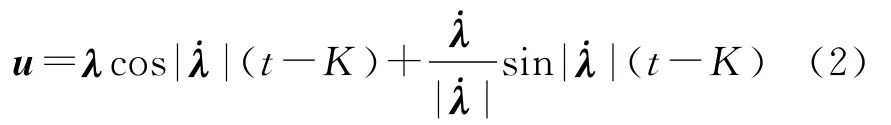
式中：K＝tgo/2，tgo是剩余飞行时间；假设α，β是计算待定拉格朗日乘子向量的中间迭代变量：

显然式（3）满足LTG控制律的必要条件是，两向量必须正交且u为推力方向单位向量还须满足边界条件。利用Jaggers[3]的预测公式，并修改与轴向视加速度aw测量信号相关的参数τ以补偿大偏航角耦合的影响：

式中：Ue是空间飞行器推力比冲。

于是可计算纵平面直角坐标参数Xp，p，Yp，p；进而预测入轨时刻的位置矢径Rp、速度模vp及当地速度倾角Θp公式：

根据理论入轨点的地心矢径、速度模和当地速度倾角边界条件，由3变量牛顿迭代公式计算当前时刻的制导变量α，β，tgo的值。于是由式（3）就可得到乘子向量；进而由式（2）计算火箭纵平面内所需的推力方向单位向量u，按向量分量表示为

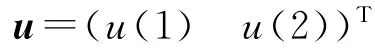
故当前满足边界条件的火箭俯仰姿态角指令应为

这里需要注意俯仰角指令的象限。

3 仿真计算与比较

为考察定点入轨控制方法对初始偏差干扰的抑制能力，这里以某飞行器参数为例，假设250km轨道高度分离的初始偏差参数如表1所示，经过大椭圆滑行，在到达22 000km高度的某时刻进行一次性直接定点入轨控制送入目标圆轨道，仿真计算比较结果如表2、表3所示。表中变量Ea，Eh，Ei，EΩ，Eω，EM分别为轨道根数长半轴、近地点高度、轨道倾角、升交点赤经、近地点幅角、平近点角的偏差，表1是假设火箭在初始时刻的轨道根数偏差，表3为入轨时刻对目标轨道的轨道根数误差，ts为滑行段的理论点火时刻，ti为实际点火时刻，Ed为实际入轨关机点与理论入轨点的距离偏差；Ex，Ey，Ez，Evx，Evy，Evz为制导坐标系中的位置坐标分量误差和速度分量误差。

表1 初始偏差工况

表2 直接定点入轨控制方法与采用标准时刻IMG方法的初始偏差仿真结果比较

表3 新的鲁棒非线性自适应控制与IMG开关六自由度仿真结果比较

从表2可以看出，对于IMG方法，按照标准点火时刻13 748s点火，由于最大初始正偏差组合和负偏差组合对入轨控制干扰很大，使得火箭关机时刻距离标准入轨点的距离分别为499.2 km和414.8km；直接定点入轨控制方法得到的点火时刻为13 441 s和13 706 s，对应的距离误差为1.625km和3.032km，速度误差也远小于IMG方法。

开关姿态控制的六自由度闭路制导仿真结果如表3所示，由于IMG方法的大偏航校正能力不足，所以在表3中的升交点赤经误差与初始误差相比没有多大改善；直接定点入轨控制方法大大消除了升交点赤经误差，所有直接坐标六分量的误差和轨道根数误差均满足要求，入轨点距离误差小于5km，实现了直接定点入轨。

比较表2和表3，姿态开关控制对定点精度只有少许影响，推力变化对定点精度的影响相对要大些，对本算例，如果推力变化5%，定点精度要下降10km。显然如果没有推力误差，理论上几乎可实现零偏差定点入轨。

由于任何一种控制方法都无法消除导航工具性误差，这里主要研究的是影响最大的初始偏差干扰与相应的定点入轨控制方法。

4 算法复杂性分析

直接定点入轨控制方法包括滑行段的点火时间、点火姿态角和偏航角限幅的开路计算和点火后的闭路制导控制。为简化实时规划，根据可能的初始偏差工况，可以先离线计算确定偏航角幅值，这样点火时间的计算利用单变量牛顿法迭代3次就可以收敛，在CPU 800M的计算机上时间小于2s，完全满足实时计算要求。这里给出的鲁棒非线性自适应闭路控制算法，由于全是解析公式，三变量牛顿迭代每次只需一步就可以逐步收敛，实时计算时间虽然长于IMG方法，但制导周期0.2s之内完全可以完成实时计算。

5 结论

提出了一种空间飞行器的直接定点入轨控制方法和算法，将点火时刻、点火姿态角和偏航角幅值作为控制变量，在滑行段计算点火参数，有效抑制了较大纵向和侧向初始偏差对入轨相位的干扰，理论上可实现直接定点入轨，具有较高的控制精度及鲁棒稳定性，可供空间飞行器远程直接交会、变轨控制参考。

[1]HANSON J M，CRUZEN M W.Ascent guidance comparisons，AIAA 1994－3568[R].1994.

[2]DENIEL T M，RUSSELL F S，SATURN V G.Navigation and targeting[J].Journal of Spacecraft，1977，14（7）：720－730.

[3]JAGGERS R F.Multi－stage linear tangent ascent guidance as baselined for the space shuttle，NASA－7239[R].1972.

[4]DANIEL R.GN＆C for pegasus air－launched space booster：design and first flight results，NASA－N911105[R].1991.

[5]LU Ping.Closed－loop endo－atmospheric ascent guidance，AIAA 2002－4558[R].2002.

[6]CALISE A J，LEE S.Design and evaluation of a three－dimensional optimal ascent guidance algorithm[J].Journal of Guidance，Control and Dynamics，1998，21（6）：867－875.

[7]GATH P F，CALISE A J.Optimization of launch vehicle ascent trajectoies with path constraints[J].Journal of Guidance，Control and Dynamics，2001，21（6）：296－306.

[8]茹家欣.液体运载火箭的一种迭代制导方法[J].中国科学E辑，2009，39（4）：696－706.RU Jia－xin.A kind of iterative guidance method for liquid launching vehicle[J].China Sciences，E Bulletins，2009，39（4）：696－706.（in Chinese）

[9]陈新民，余梦伦.迭代制导在运载火箭上的应用研究[J].宇航学报，2003，24（5）：10－16.CHEN Xin－min，YU Meng－lun.The application research of iterative guidance method [J].Journal of Astronautics，2003，24（5）：10－16.（in Chinese）

[10]李华滨，李伶.小型固体运载火箭的迭代制导方法研究[J].航天控制，2002，20（2）：29－37.LI Hua－bing，LI Ling.The research of iterative guidance method for small solid rocket vehicle[J].Aerospace Control，2002，20（2）：29－37.（in Chinese）

[11]韩祝斋.用于大型运载火箭的迭代制导方法[J].宇航学报，1983，4（1）：10－16.HAN Zhu－zhai.An iterative guidance method for large launching vehicle[J].Journal of Astronautics，1983，4（1）：10－16.（in Chinese）

[12]刘新建.火箭入轨的大偏航鲁棒非线性控制方法[J].固体火箭技术，2012，35（4）：434－437.LIU Xin－jian.A robust nonlinear self－adaptive control method with large yaw for rocket orbital insertion[J].Journal of Solid Rocket Technology，2012，35（4）：434－437.（in Chinese）