脉冲修正弹参数优化设计方法
2013-12-25常思江曹小兵王中原宇文聪伶
常思江,曹小兵,王中原,宇文聪伶
(1.南京理工大学 能源与动力工程学院,南京210094;2.无锡职业技术学院 控制技术学院,江苏 无锡214121;3.西北工业集团有限公司 科研一所,西安710043)
随着低间接伤害概率和高精度打击逐渐成为现代战争对弹药武器的基本要求,发展低成本弹道修正技术已成为提高火炮武器系统作战效能的重要途径之一。其中,一类采用脉冲发动机作为控制执行机构的弹道修正弹因成本较低、易于工程实现等受到了国内外的广泛关注[1-5]。
在此类脉冲修正弹的研究过程中,在其初步设计阶段合理、有效地确定相关参数(如脉冲参数、弹道参数等)是极为重要的问题,国内外也开展了相应的研究。文献[3]中以落点圆概率误差为评判标准,采用蒙特卡罗方法,通过大量的数值仿真对脉冲个数、单脉冲冲量大小等参数进行了设计;文献[4]分别对修正阈值、脉冲力值、脉冲个数对脱靶量的影响进行了仿真分析,以此作为确定脉冲末修迫弹参数的主要依据;文献[5]则利用数值仿真拟合出了脉冲工作级数、修正时机等参数与修正距离的数学关系式。
根据上述文献,该类脉冲修正弹箭的参数设计主要还是依靠大量不同条件下的数值仿真。该方式操作简易,但对设计者的水平、经验等依赖较大,缺乏较强的理论支撑,且实际中难以穷尽所有条件,其结果存在一定的局限性。对此,本文以某低速旋转尾翼式脉冲修正弹为对象,根据其特点建立了一个脉冲修正弹参数优化设计模型,并提出一个基于自适应罚函数且适于处理整数离散变量的改进粒子群算法,对某些主要参数(如脉冲个数、单脉冲冲量大小等)进行了寻优,旨在为脉冲修正弹的参数设计提供一个新的思路和方法。
1 脉冲修正弹参数优化设计模型
1.1 优化设计变量与目标函数
脉冲修正弹的设计参数主要包括脉冲发动机个数、单脉冲冲量大小、单个脉冲持续作用时间、脉冲发动机在弹体上的布局参数及弹体转速等,它们对弹箭的弹道特性都有不同程度的影响,这些影响有时彼此之间相互制约,这也是开展参数优化设计的必要性所在。由于旨在讨论思路和方法,为方便起见,本文选取脉冲发动机个数n、单脉冲冲量大小Iimp、脉冲发动机相对于弹体质心的轴向布置位置(即轴向偏心距离)Limp及弹体尾翼斜置角εw为优化设计变量,而其余一些参数(如单脉冲持续作用时间tp等)则根据相关试验或经验取为定值。
考虑到脉冲修正弹的低成本特点及修正能力要求,选取脉冲发动机总冲量IT为优化目标函数,在寻优过程中,应遵循一定原则寻求一组优化设计变量使脉冲修正弹所用总冲IT最小,该目标函数反映了设计方案对修正低能耗的要求。
1.2 优化模型的约束条件
约束函数是对设计变量取值予以某些限制的数学关系式,或是对优化设计问题本身提出的条件限制。根据脉冲修正弹的特点,对优化设计模型提出如下约束条件。
①脉冲个数和单脉冲冲量大小约束。
对于本文研究的脉冲修正弹,多个脉冲发动机沿弹体周向均匀布置,由于弹体直径有限,并考虑到工程中脉冲发动机喷口的尺寸以及弹体材料的强度约束,取脉冲发动机个数约束为nmin≤n≤nmax(n为偶数);而单个脉冲发动机的冲量与火药类型、装药量等有关,取单脉冲冲量约束为0<Iimp<Iimp,max。
②脉冲发动机轴向偏心距约束。
脉冲发动机的轴向偏心距影响弹箭在脉冲作用下受到的脉冲作用力矩的大小和方向,故与脉冲修正弹的修正能力和飞行稳定性都有直接关系,这里取轴向偏心距约束为0≤Limp≤Limp,max。
③弹箭飞行攻角约束。
弹箭在无控及有控飞行过程中的攻角α均不能超过一定的限制,即α≤αmax。
④弹体转速约束。
本文研究的是一种低旋尾翼弹,故在设计弹体转速时须考虑避免共振的不利影响,由外弹道理论,低旋尾翼弹转速应至少大于2倍的共振转速R;若弹体滚转一周内若干脉冲接续作用完毕,则弹体在脉冲持续作用时间tp内所转过的角度应小于脉冲发动机喷口间的夹角2π/n。设弹体平衡转速为L,则有

由于弹体平衡转速与尾翼斜置角εw有关,因此,弹体转速约束实质上也是优化设计变量εw和n之间的约束关系。尾翼斜置角和平衡转速的关系:

式中:v为 弹 箭 速 度;kxw=ρSlm′xw/(2C),kxd=ρSldm′xd/(2C),其中ρ为大气密度,S为弹体特征面积,l为弹体特征长度,d为弹径,C为弹体极转动惯量,m′xw为尾翼导转力矩系数导数,m′xd为极阻尼力矩系数导数。
将式(2)代入式(1),可得:

式(3)反映了优化设计变量εw和n之间的约束关系。
⑤修正能力约束。
修正能力是弹道修正弹最重要的技术指标之一。因此,在寻优过程中除需满足以上约束条件外,为合理地配置资源,还要保证弹箭的实际修正能力Xa与需求修正能力Xd相匹配,Xd值可通过对弹箭无控散布或目标运动特性的分析予以确定。修正能力的约束表达式为

式中:κ为需求修正能力的放大系数,κ≥1.0;σ表示精度要求,为一适当小的正数。
1.3 优化模型分析及求解方法选取
综上所述,可将脉冲修正弹参数优化设计模型写成如下形式:

式中:E4表示设计变量的四维欧氏空间,gi(x)表示优化模型中的不等式约束。
根据模型(5),该优化问题为有约束混合整数非线性规划问题(MINLP),这类问题中的设计变量既有连续变量又有整数离散变量,且约束的存在要求寻优时不仅要使目标函数不断趋于极值,还要实时检验解的可行性,故MINLP的求解比一般有约束优化问题复杂得多,有必要寻求适配的求解方法。目前,处理MINLP的方法可分为随机方法和确定方法,其中,随机方法可同时处理连续变量和整数离散变量,并能借助评价函数引导寻优。因此,本文提出采用一种随机方法即粒子群算法[6]对优化设计模型(5)进行寻优。下面将讨论一种基于自适应罚函数的改进粒子群算法。
2 基于自适应罚函数的改进粒子群算法
2.1 标准粒子群算法SPSO2011
粒子群算法自1995年提出以来,经各国学者不断应用和研究,提出了多种改进。这里介绍由法国学者Maurice Clerc于2011年提出的标准粒子群算法SPSO2011[7],其要点如下:
①采用自适应随机拓扑方法确定出每个粒子的邻域。
②SPSO2011的速度更新公式为

式中:q为迭代次数;i代表粒子;vi(q)表示粒子i迭代q次后的速度;pi(q)表示粒子i迭代q次后的位置;w表示惯性权重;p′i(q)为超球面内服从均匀分布的随机点。
③边界约束定义了各优化变量的定义域[pi,min,pi,max],最优值包含其中,当粒子越界时,将越界那一维的速度设为零,并将其位置作为边界值。
④和普通标准粒子群算法一样,SPSO2011在粒子初始化和速度更新时也要用到随机数,为了提高生成随机数的质量并降低寻优失败率,本文将采用文献[8]中提出的KISS伪随机数发生器。
2.2 自适应罚函数的构造
罚函数方法是化有约束问题为无约束问题的常用方法,而自适应罚函数法能够利用寻优过程中的反馈信息动态地调整罚因子,故学界普遍认为该方法的寻优效果更佳。目前,关于自适应罚函数法的研究大多集中于进化算法(如遗传算法等)领域。尽管进化算法与粒子群算法的原理、实现方式等差异较大,但基于两者均属于概率随机方法这一事实,本文借鉴进化算法中自适应罚函数[9]的构造思想,提出一种带有自适应罚函数的改进粒子群算法。自适应罚函数构造如下。
设各粒子所表示的设计变量分别为X1,X2,…,Xs,整个群体的目标函数平均值为(X),则对Xi构造如下自适应惩罚函数F(Xi):

式中:m为约束的个数;vj(Xi)表示粒子Xi对第j个约束函数的违反值,其表达式为
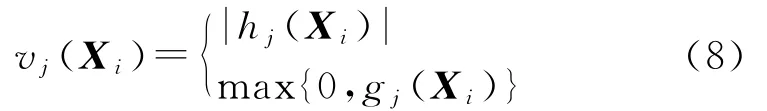
而

对不可行粒子,惩罚函数将根据个体和整个群体的适应值信息和约束违反程度动态地调节惩罚强度。
2.3 整数离散变量的处理
在脉冲修正弹参数优化设计问题中,脉冲个数必须为整数,但在初始化和迭代更新时粒子位置无法保证一定是整数,故必须取整。常用方法是直接取最近的整数,但此方法可能会导致最终无法获得最优解。这里参考文献[10],采用一个简单可行的随机取整策略。
设整数变量在实数空间更新时为r值,取整时将从相邻整数floorr和ceilr中随机选取,ceilr和floorr分别表示向上和向下取整,而被选概率与其至r的距离成反比。以Intr表示对r取整,有
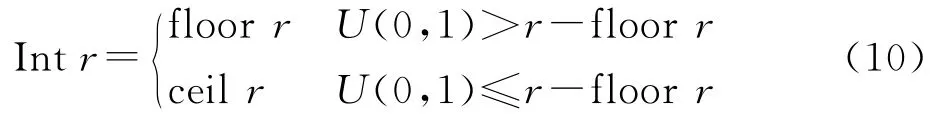
式中:U(0,1)为[0,1]内均匀分布的随机数。
3 算例仿真及结果
为了验证以上改进粒子群算法的效果,本文选取了7个广泛应用于各类智能算法(如模拟退火算法、遗传算法等)性能测试的Benchmark函数[11]进行检测,全部得到了高质量的最优解(与精确解相比最大误差约为0.002%),故可将其应用于脉冲修正弹参数的优化设计。
改进粒子群算法的主要参数及优化变量取值范围分别列于表1和表2中。表1中:NT为粒子总数,NH为随机拓扑结构中的粒子数,w为惯性权重,c为加速系数上限值。

表1 改进粒子群算法主要参数取值

表2 优化设计变量的取值范围
根据某制式弹的散布特性,本文以侧向弹道修正为例,取修正弹的最大修正能力约束为50m;弹体飞行过程中最大攻角限幅αmax=6°;初速v0=420m/s,射角θ0=45°;脉冲启控点为距离落点1 000m斜距处,单脉冲持续作用时间tp=20ms。
对改进粒子群算法编制程序进行寻优,得到设计变量的优化值:脉冲发动机个数为10,单个脉冲发动机冲量为18N·s,脉冲发动机布置的轴向偏心距为0.025m,弹体尾翼导转角为0.244rad。相应地,目标函数即脉冲发动机总冲为180N·s。

表3 某脉冲修正弹的参数优化设计结果
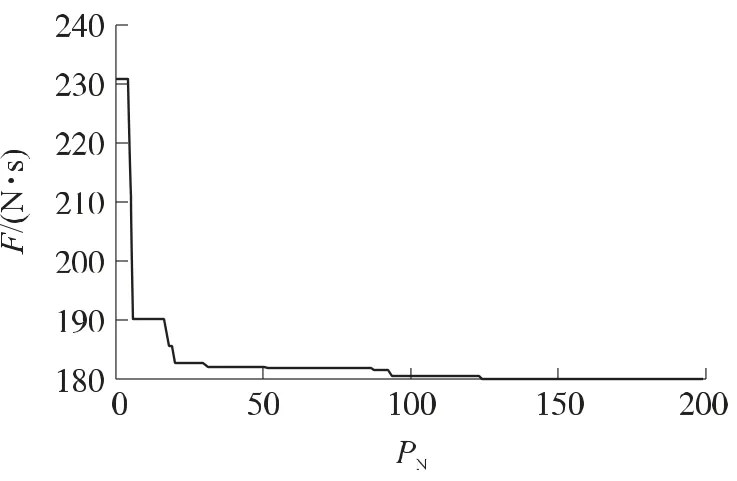
图1 寻优过程中罚函数值的收敛曲线

图2 优化变量对应的修正弹道侧偏曲线

图3 优化变量对应的修正弹道攻角幅值
根据表3和图1,改进粒子群算法的多次寻优结果略有差异,这是由于该类算法属于随机优化方法,其优化结果必然表现出一定的随机特性,但从总体上看,多次优化所得最优罚函数值和最优目标函数值的变化不大,几乎不影响实际应用的效果。
从单次的粒子群寻优过程来看,自适应罚函数值在寻优的最初阶段下降很快,随着粒子的不断进化,罚函数值的降低越发趋缓,当粒子的进化代数为30左右时,罚函数值已趋于一定值,体现了良好的收敛性。由图2、图3可看出,采用改进粒子群算法寻优所得优化变量所对应的修正弹道诸元也可满足约束的要求。以上结果表明,采用基于自适应罚函数的改进粒子群算法求解脉冲修正弹参数优化设计模型,收敛较快且优化效果较好。
4 结束语
通过建立并采用适配方法数值求解脉冲修正弹参数的优化设计模型,可得到以下结论:①选取若干与脉冲、飞行弹道等相关参数作为设计变量,并在一定约束和目标函数条件下进行参数优化设计,是一种合理、有效且理论性较强的设计方法;②提出的基于自适应罚函数的改进粒子群算法适于求解脉冲修正弹参数优化设计这类有约束混合整数非线性规划问题,计算结果表明,该算法收敛快速且精度可靠。研究结果为该类弹箭的参数设计提供了新的思路和方法。
[1]CORRIVEAU D,BERNER C,FLECK V.Trajectory correction using impulse thrusters for conventional artillery projectiles[C]//IBC.23rd International Symposium on Ballistics.Tarragona,Spain:IBC,2007:639-646.
[2]徐劲祥.末段修正迫弹脉冲控制方案研究[J].弹箭与制导学报,2005,25(1):50-52.XU Jin-xiang.Study on impulse correction scheme of terminal correction mortar projectiles[J].Journal of Projectiles,Rockets,Missiles and Guidance,2005,25(1):50-52.(in Chinese)
[3]JITPRAPHAI T.Lateral pulse jet control of a direct fire atmospheric rocket using an inertial measurement unit sensor system[D].Oregon:Oregon State University,2001.
[4]徐劲祥,夏群力.末段修正迫弹主要参数确定方法研究[J].弹箭与制导学报,2005,25(2):80-82.XU Jin-xiang,XIA Qun-li.Study on primary parameters determination methods of terminal correction mortar projectiles[J].Journal of Projectiles,Rockets,Missiles and Guidance,2005,25(2):80-82.(in Chinese)
[5]姚文进,王晓鸣,李文彬,等.弹道修正引信脉冲修正参数研究[J].制导与引信,2007,28(2):24-27.YAO Wen-jin,WANG Xiao-ming,LI Wen-bin,et al.Research on the pulse correction parameters for trajectory correction fuze[J].Guidance and Fuze,2007,28(2):24-27.(in Chinese)
[6]ENGELBRECHT A P.计算群体智能基础[M].谭营,译.北京:清华大学出版社,2009.ENGELBRECHT A P.Fundamental of swarm intelligence algorithm[M].Beijing:Publishing Company of Tsinghua University,2009.(in Chinese)
[7]CLERC M.Standard particle swarm optimization from 2006to 2011 [EB/OL].(2011-07-13)[2011-7-20].http://clerc.maurice.free.fr/pso/SPSO_descriptions.pdf.
[8]MARSAGLIA G,ZAMAN A.The kiss generator[R].Tallahassee,FL:Florida State University,1993.
[9]HITOSHI I.Frontiers in evolutionary robotics[M].Vienna:ITech Education and Publishing,2008.
[10]王金华,尹泽勇.一个约束离散优化问题的粒子群算法研究[J].计算机工程与应用,2008(3):242-244.WANG Jin-hua,YIN Ze-yong.Solving constrained discrete optimization problem with particle swarm optimizer[J].Computer Engineering and Applications,2008(3):242-244.(in Chinese)
[11]YAN L,SHEN K,HU S.Solving mixed integer nonlinear programming problems with line-up competition algorithm[J].Computers & Chemical Engineering,2004,28(12):2 647-2 657.
