稳健优化在导弹启控点选择中的应用
2013-12-25朱大林唐胜景熊俊辉
朱大林,唐胜景,郭 杰,熊俊辉
(北京理工大学 宇航学院,北京100081)
对于具有无控起飞段的导弹,实际飞行中由于受到各种随机干扰的影响,其启控点弹道参数是随机分布的,从而形成相对于理论启控点的散布。为了保证导弹受到良好的控制,启控点散布应满足制导系统开始导引的要求。如对于激光驾束制导的反坦克导弹,一般要求启控点要落入规定的光束截面内。导弹启控点的选择一般是期望启控点落入规定的区域内,并期望启控点波动越小越好,这两点一般可以通过启控点弹道参数的期望和方差进行描述。为达到这2个目标,通常需要不断地进行统计分析和筛选,以确定合适的启控距离或时间以及相关总体参数(如初速度、发射角等)。文献[1-2]采用Monte Carlo法对反坦克导弹的启控点散布进行了研究,其中文献[2]通过多次仿真确定了最佳的发射角;文献[3]采用协方差分析描述函数法建立弹箭外弹道的随机优化模型,并通过优化算法确定了偏角方差最小时有关总体参数的取值。上述方法虽然都可以用于导弹的启控点选择,但其不足之处为:统计分析效率比较低,筛选过程比较费机时;优化目标中没有同时考虑优化条件对散布均值和方差的影响。
针对上述问题,本文采用稳健优化的概念和方法处理导弹启控点的选择问题,综合考虑启控距离(时间)和总体参数的取值对启控点散布的影响。稳健优化(Robust Optimization)是产品质量工程中保证产品质量稳定的一种重要的设计方法,其基本思想就是通过优化算法在可行域内寻找最佳的设计方案,力图使产品的质量特性均值尽可能地接近目标值,同时对干扰因素引起的波动尽可能地小[4]。可见,稳健优化与导弹启控点选择的目的是一致的。本文根据稳健优化响应面建模的思想首先对导弹扰动运动系统建立高斯型径向基网络(Gaussian Radial Basis Network,GRBN),并以GRBN为基础给出不确定性分析的解析表达式;然后以某反坦克导弹启控点选择的要求为例建立稳健优化模型,并采用小生境Pareto遗传算法获得该模型的Pareto最优解集。对最优解进行Monte Carlo模拟打靶验证表明,优化结果比较令人满意,从而为弹道设计、制导系统设计等提供参考和依据。
1 可控因素和噪声因素的确定
影响导弹启控点散布的因素有很多种,如初始扰动、推力偏心、弹体质量分布不对称、风、制造和安装工艺误差等。一般认为这些因素是随机分布的,事先可以根据试验数据或经验确定其分布类型。为了区别对待这些因素,根据稳健优化的概念可将其分为两大类:可控因素和噪声因素。可控因素就是可以选择其水平即名义值的因素,也是设计变量,通常由设计名义值和设计容差进行描述;噪声因素就是不可控的因素,通常由其分布类型及数字特征进行描述。因此,导弹启控点选择的稳健优化就是在约束范围内确定可控因素的最佳水平组合。
以某反坦克导弹的启控点选择为例,假设初步考虑的因素有:初速度v0,发射角θ0,初始滚转角速度ωx0,加速发动机点火时间tb,启控距离xc,初始弹道偏角ψv0,惯性中心主轴在弹体坐标系下的方位角λ和μ以及横风wz。如果其水平可以选择的因素有初速度v0,发射角θ0,初始滚转角速度ωx0,加速发动机点火时间tb以及启控距离xc,则确定的可控因素x和噪声因素ω分别为x=(v0θ0ωx0tbxc),ω=(ψv0λμ wz)。这些因素的详细描述分别如表1和表2所示。

表1 可控因素

表2 噪声因素
2 扰动运动系统建模和不确定性分析
确定了影响因素之后,接下来就是对导弹扰动运动系统进行统计分析,从而为第3节的稳健优化做准备。导弹扰动运动系统的数学模型可参考文献[5],常用的分析方法有 Monte Carlo法和协方差分析描述函数法。Monte Carlo法是启控点散布分析方法中一种简单而有效的方法,但为了获得精确的统计值,通常需要几百次甚至上千次的模拟打靶,比较费机时。协方差分析描述函数法是运用描述函数理论将原来的非线性随机系统进行统计线性化,通过求解导出的关于状态变量均值和协方差的传播方程,从而获得相应的统计值[6]。这种方法可以明显提高统计分析的效率,但目前统计线性化的理论主要是建立在状态变量服从联合正态分布的假设上,当原系统非线性程度比较高或状态变量严重偏离正态分布时,协方差分析描述函数法的分析精度会明显降低;而且,这种方法求解的微分方程比较多,不利于后续的稳健优化。基于上述讨论,借鉴稳健优化响应面建模的思想,对导弹扰动运动系统采用GRBN进行拟合,并在此基础上给出不确定性分析的解析表达式,这种方法可以显著提高统计分析的效率。
2.1 GRBN建模
径向基函数网络是一种简单而有效的建模工具,其中GRBN由于可以写成便于概率积分的张量积函数形式[7],因而在文中被选用。GRBN的数学模型可写为
式中,‖·‖为欧氏范数,x=(x1x2…xn),为n维输入向量;x1,x2…,xm为径向基网络中心点;α0为常数项;α=(α1α2…αm),为权系数向量,c为正的常实数。
GRBN的构造就是要确定网络的结构和参数,其训练过程可参考一般径向基函数神经网络的学习算法[8-9]。对于本文的导弹扰动运动系统,GRBN的构造过程为:首先选用合适的试验设计获得以可控因素和噪声因素为试验点、以启控点参数为输出的样本;其次,对样本进行分析,剔除一些离群点;最后,随机选择一部分样本试验点作为GRBN的中心点并通过Levenberg-Marquardt优化算法极小化样本的误差平方和,从而确定GRBN的α0,α和c。GRBN的拟合精度可以通过重采样样本进行检验,常用的检验准则有相对平均绝对误差检验准则和相对最大误差检验准则[10]。
2.2 基于GRBN的不确定分析
GRBN满足拟合精度要求后,就可以对其进行不确定性分析。将式(1)改写为
式中:xj为点x的第j个分量,xij为点xi的第j个分量。令
则
假设可控因素、噪声因素彼此相互独立,则根据文献[7]的推导,式(3)输出的均值和方差可表示为
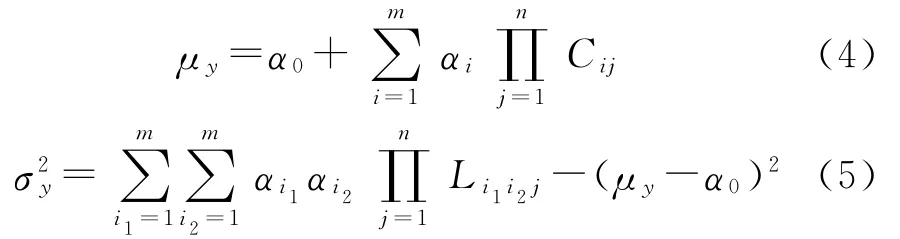
对于形式为式(1)的GRBN,经过推导可得到如下结果:
若因素xj服从均匀分布,即
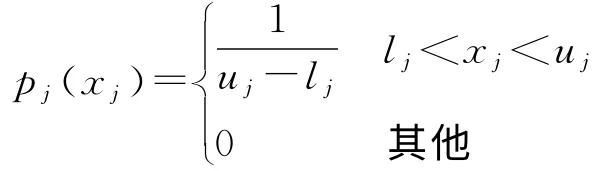
则
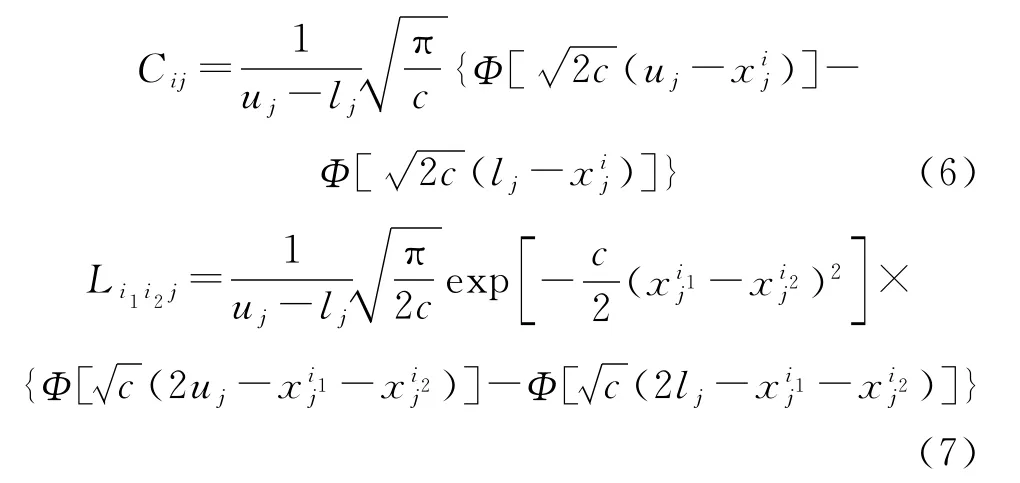
式中:Φ(·)为标准正态分布的分布函数。
若因素xj服从正态分布,即
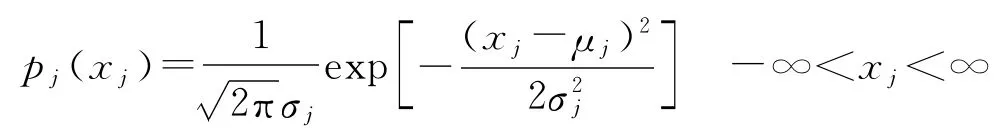
则
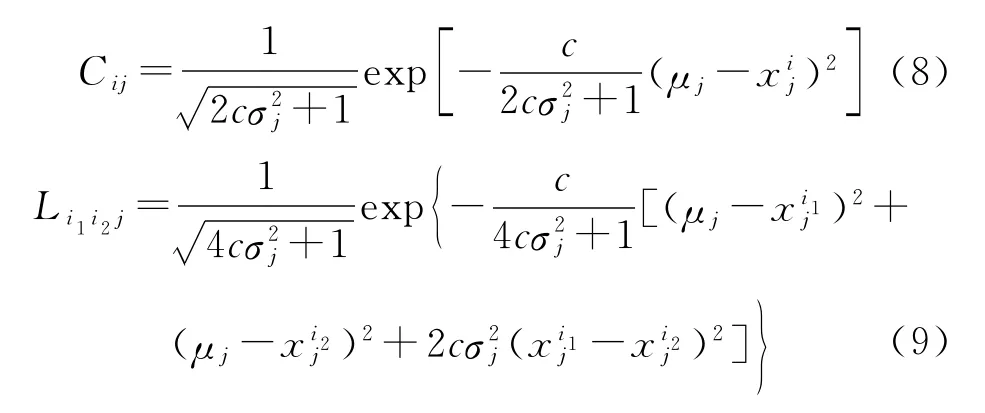
3 启控点选择的稳健优化模型与求解
与确定性优化模型不同,稳健优化模型一般是采用概率论的术语进行描述的,比较常用的就是随机变量的均值和方差。下面以第1节提到的反坦克导弹为例,建立启控点选择的稳健优化模型。
通常,反坦克导弹的发射角不太大,初始段弹道比较低。在选择启控距离和总体参数时,一般期望启控点的方向偏差和散布半径比较小,并期望启控点有一定的高度且弹道角落入一定的范围内,以防止其掉地或启控后飞离视场范围。根据这些要求,建立的稳健优化模型为
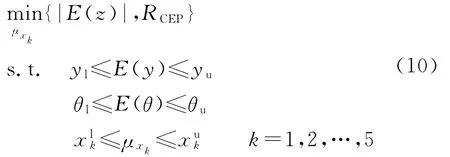
式中:E(·)表示随机变量的期望;μxk为可控因素xk的名义值;yl,yu为高度界限;θl,θu为弹道角界限为可控因素名义值的界限;RCEP为圆概率误差半径,可采用如下公式进行计算[11]:

式中:σy,σz分别为启控点的高度和方向均方差。
需要指出的是,如果希望稳健优化模型中某个约束具有一定的稳健性,可以通过引入方差进行调整。例如:如果希望高度约束具有一定的稳健性,可以将其修改为yl+nlσy≤E(y)≤yu-nuσy,式中:nl,nu称为σ水平。
求解上面建立的稳健优化模型,其实就是求解一个多目标优化问题。多目标优化问题的求解策略大致分为两类,可将其转化为单目标优化问题或者直接求解多目标优化问题,每种优化策略又有不同的优化方法。这里采用小生境Pareto遗传算法直接求解建立的稳健优化模型。该算法采用Pareto支配关系进行锦标赛选择,并采用小生境技术实现群体的多样性,能较好地获得稳健优化模型的Pareto最优解集,从而方便设计者根据自己的偏好进行挑选,算法的具体描述可参考文献[12]。
4 算例仿真
下面仍以第1节提到的反坦克导弹启控点选择为例,假设瞄准线水平,根据第3节建立的具体稳健优化模型为
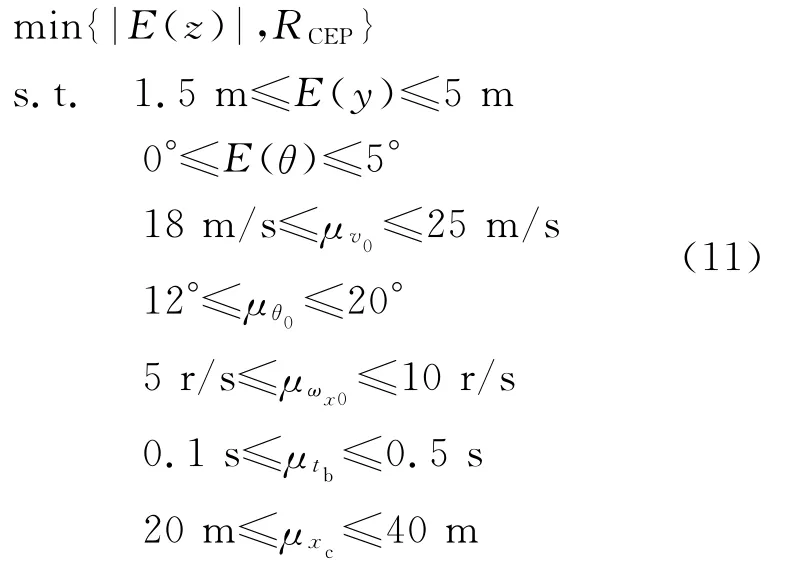
为了利用式(4)和式(5)进行不确定性分析,首先需要对导弹扰动运动系统构造GRBN。这里选用拉丁超方试验设计选择500个试验点,通过对扰动运动系统的仿真获得启控点坐标y,z和弹道角θ的取值。随后通过分析样本剔除一些离群点,形成样本容量为491的样本。在构造以启控点坐标y,z和弹道角θ为输出的GRBN时随机选择75%的试验点作为GRBN的中心点。GRBN的拟合精度通过重采样300个样本点进行检验,其相对平均绝对误差均小于7%。
GRBN满足使用要求后,接着采用式(11),优化算法设置5个子种群,共500个个体,种群进化100代,最后共获得181个Pareto非支配解,形成的Pareto前沿如图1所示。
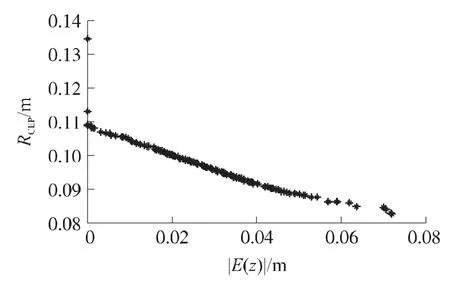
图1 Pareto前沿
为验证优化结果的可信性,从上述Pareto非支配解解集中随机挑选出一个解对原扰动运动系统进行500次Monte Carlo模拟打靶验证。挑选的解为μv0=24.15m/s,μθ0=12.94°,μω0=9.18r/s,μtb=0.10s,μxc=21.93m。
验证结果如表3所示,通过 Monte Carlo模拟打靶获得的散布图如图2所示。
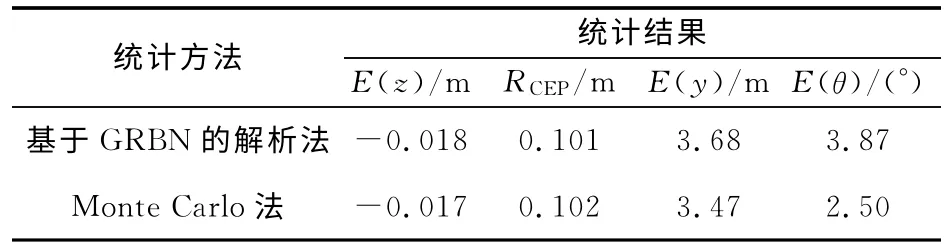
表3 验证结果
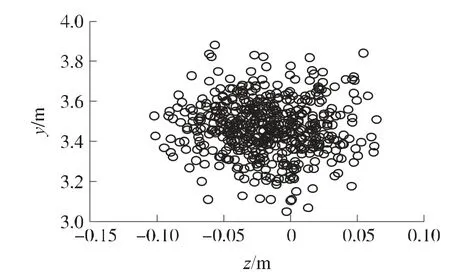
图2 散布图
由表3的验证结果可以看出,除了E(θ)的数值相对有所偏大之外,其余的统计值基本上比较接近,启控点高度和弹道倾角的均值均在约束范围之内。从图2的散布分布来看,这组解达到了预期的目的。
5 结论
本文采用稳健优化的思想和方法处理导弹启控点选择的问题,从仿真验证的结果来看,这种做法是可行的。文中采用小生境Pareto遗传算法可以获得启控点稳健优化模型的Pareto最优解集,从而为弹道设计者提供更多的参考和选择。本文仍需改进的地方就是在优化过程中需要提高GRBN的局部拟合精度从而进一步提高稳健最优解的可信度。
[1]LIU Yang,LI Kun,SONG Xiao-dong,et al.Monte Carlo ballistic simulation applied to dispersion analysis of starting control points for antitank missile[C]//Proceedings of 2011 International Conference on Electronic and Mechanical Engineer and Information Technology.Piscataway:IEEE Computer Society,2011:2 929-2 932.
[2]闫智强,周凤歧,周军.基于 Monte Carlo的激光驾束反坦克导弹 启 控 点 散 布 研 究 [J].弹 箭 与 制 导 学 报,2005,26(1):689-691.YAN Zhi-qiang,ZHOU Feng-qi,ZHOU Jun.The study to the spread of starting control points for laser beam-rider guidance anti-tank missile on Monte Carlo method[J].Journal of Projectiles,Rockets,Missiles and Guidance,2005,26(1):689-691.(in Chinese)
[3]徐明友,丁松滨,徐直军.外弹道优化设计的随机模型[J].南京理工大学学报,1997,21(5):403-406.XU Ming-you,DING Song-bin,XU Zhi-jun.Random model for optimum design of exterior ballistics[J].Journal of Nanjing U-niversity of Science and Technology,1997,21(5):403-406.(in Chinese)
[4]陈立周,于晓红,翁海珊.基于随机优化的工程稳健设计[J].北京科技大学学报,1999,21(1):57-59.CHEN Li-zhou,YU Xiao-hong,WENG Hai-shan.Robust engineering design by stochastic optimization[J].Journal of University of Science and Technology Beijing,1999,21(1):57-59.(in Chinese)
[5]钱杏芳,林瑞雄,赵亚男.导弹飞行力学[M].北京:北京理工大学出版社,2006:136-154.QIAN Xing-fang,LIN Rui-xiong,ZHAO Ya-nan.Missile flight mechanics[M].Beijing:Beijing Institute of Technology Press,2006:136-154.(in Chinese)
[6]袁子怀,钱杏芳.有控飞行力学与计算机仿真[M].北京:国防工业出版社,2001:139-174.YUAN Zi-huai,QIAN Xing-fang.Control flight mechanics and computer simulation[M].Beijing:National Defence Industry Press,2001:139-174.(in Chinese)
[7]CHEN Wei,JIN Rui-chen,SUDJIANTO A.Analytical variance-based global sensitivity analysis in simulation-based design under uncertainty[J].Journal of Mechanical Design,2005,127(5):875-886.
[8]UYKAN Z,GUZELIS C,CELEBI M E.Analysis of inputoutput clustering for determining centers of RBFN[J].IEEE Transactions on Neural Networks,2000,11(4):851-858.
[9]CHEN S,COWAN C F N,GRANT P M.Orthogonal least squares learning algorithm for radial basis function network[J].IEEE Transactions on Neural Networks,1991,2(2):302-309.
[10]龙腾.飞行器多学科设计方法与集成设计平台研究[D].北京:北京理工大学宇航学院,2009.LONG Teng.Research on methods of multidisciplinary design optimization and integrated design[D].Beijing:School of Aerospace Engineering,Beijing Institute of Technology,2009.(in Chinese)
[11]韩子鹏.弹箭外弹道学[M].北京:北京理工大学出版社,2008:113-116.HAN Zi-peng.Projectile and rocket exterior ballistics[M].Beijing:Beijing Institute of Technology Press,2008:113-116.(in Chinese)
[12]HORN J,NAFPLIOTIS N,GOLDBERG D E.A niched Pareto genetic algorithm for multiobjective optimization[C]//Proceedings of the First IEEE Conference on Evolutionary Computation.New York:IEEE,1994:82-87.
