基于Logvinovich原理射弹超空泡形态解析解研究

李魁彬，王安稳，施连会，邓 磊

（海军工程大学 理学院，武汉430033）

国内外针对射弹超空泡形态已有许多研究，其计算主要通过由实验数据拟合的经验公式[1－3]、CFD软件仿真[4]和基于Logvinovich原理的数值计算[5－7]3 种 途 径。 本 文 基 于 Logvinovich 原 理、Riabouchinsky[8]空泡闭合模型和射弹动力学方程，通过适当简化，推导出射弹运动过程中空泡形态解析解和空泡参数的计算公式。计算结果与经验公式吻合良好，说明本文推导的正确性。

1 方程的建立

1.1 参考坐标系

超空泡射弹高速运动，重力的作用可以忽略，其运动轨迹近似为直线[9]。本文主要研究水平直航的射弹。空间上，以射弹初始点为原点O，以射弹空化器为原点o，X、x轴正方向均为运动方向，分别建立如图1所示的惯性坐标系OXY和弹体坐标系oxy。时间上，以初始时刻为零点，建立绝对时间轴t；以射弹空化器运动处的时刻为零点，建立与绝对时间轴方向相反的相对时间轴tx。

图1 坐标系和空泡扩展示意图

1.2 Logvinovich独立扩展方程

Logvinovich基于势流理论提出了空泡截面独立膨胀原理[2，10]，其在绝对坐标系下数学方程为

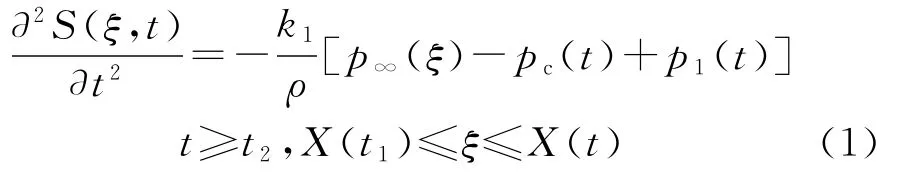
式中：ξ＝X（t2），S（ξ，t）为ξ处t时的空泡面积；k1＝4π/A2，A为微弱依赖于空泡数σ的系数，通常取经验常数2；p∞（ξ）为与ξ处于相同水平面无穷远处的压强；pc（t）为空泡内压强，在自然超空泡中，pc（t）为饱和蒸汽压pc；p1（t）为外部瞬时扰动压强；X（t1），X（t）分别为射弹首端运行到空泡闭合处的时间t1、到达空泡开始处的时间t时在X轴上的坐标。

空泡扩展的初始条件为

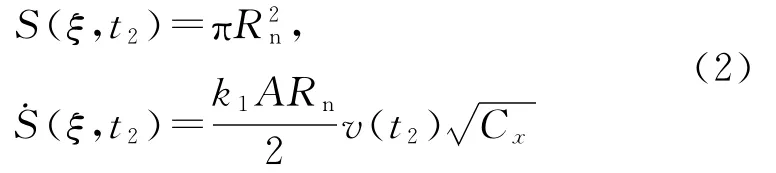
式中：Rn为射弹空化器半径；v（t2）为空化器通过截面ξ时的速度；Cx＝Cx0（1＋σ），为阻力系数，Cx0为σ＝0时的阻力系数，对于圆盘空化器，Cx0＝0.827。

1.3 超空泡航行体动力学方程

水平直航超空泡射弹的动力学方程为

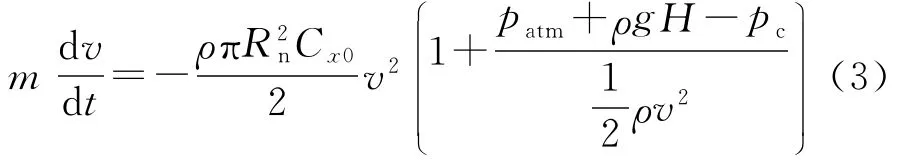
式中：m为射弹质量，patm为大气压，H为射弹在水中的深度，v为射弹速度。

1.4 空泡闭合模型

空泡尾部闭合采用Riabouchinsky模型，当空泡截面积等于空化器面积时空泡闭合。

2 公式简化及推导

不考虑外部瞬时扰动压强p1（t），根据坐标系之间的关系，对于射弹，将式（2）代入，式（1）在弹体坐标系下可化为

式中：Δp＝p（ξ）－pc，p（ξ）＝patm＋ρgH，tx为相对时间轴下的时间。

结合空泡闭合模型得：不考虑瞬时扰动压强，完整自然超空泡的扩展时间等于空泡闭合处空泡截面从空泡产生到空泡闭合的扩展时间，仅依赖于航行体经过空泡闭合处时的参数；空泡最大长度由扩展时间和航行体在这段时间的运动决定。完整空泡扩展时间公式为

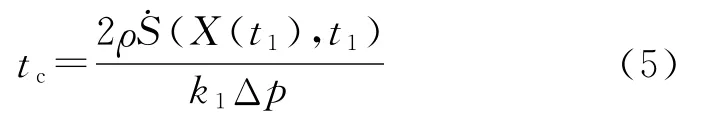
求解方程（3）得射弹的位移和速度的解析解：

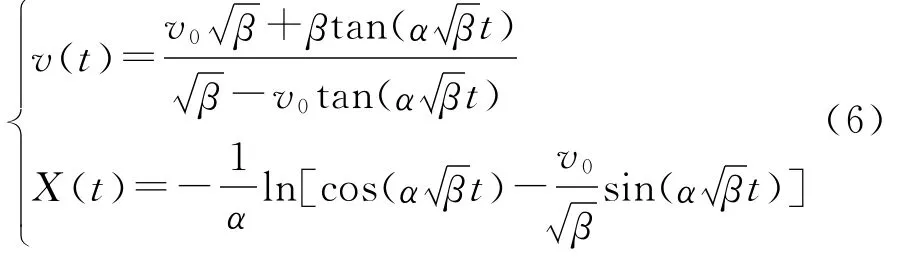
式中：α＝－ρSnCx0/（2m），β＝2Δp/ρ，v0为射弹初始速度，Sn为空化器面积。

考虑完整空泡扩展时间非常短，高速下压差影响较小，可忽略。空泡扩展过程中射弹位移和速度的解析解为

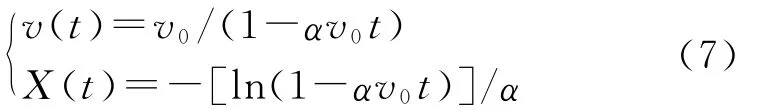
通过坐标变换，得到相对时间轴下射弹的速度和弹体坐标系下的横坐标：

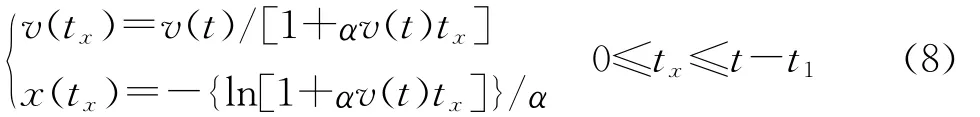
式中：v（t）为t时空化器的速度，v（tx）为t2时空化器速度，t2对应于相对时间轴的tx。

联立式（4）和式（8）得射弹速度v（t）时弹体坐标系下空泡形态横、纵坐标公式：

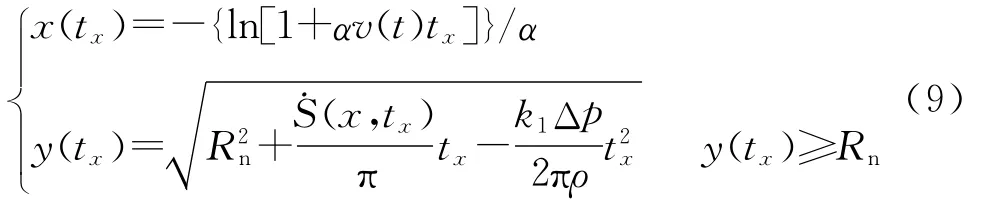
式（6）、式（9）和式（10）组成了射弹运动过程中任意时刻超空泡形态计算公式。

考虑完整空泡扩展过程中Cx变化很小，Cx≈Cx｜t＝0，可得空泡的参数公式。

考虑空泡在射弹尾部闭合，从超空泡变为局部空泡时 的 空 泡 数：σ＝γ/（4e2αl－4eαl），其 中，γ，l为射弹长度。

空化器周围，eαx－1≈αx，空泡数对空泡半径影响很小，可以忽略，式（10）可化为近似“1/3法则”的公式：

3 算例和分析

取参数Rn＝0.001 m，m＝0.15kg，l＝0.06 m，v0＝1 000m/s，patm＝0.101MPa，pc＝2 350Pa，H＝1m。

分析射弹首尾压差对速度的影响，如图2所示。射弹速度越大，深度越小，首尾压差对速度影响越小；当v≥100 m/s，H≤100 m 时，其影响可以忽略；当射弹速度较小、深度较大时，计算需要考虑压差的影响。

图2 射弹速度随时间的变化

Savchenko[1]根据试验提出适用于空泡数0.012～0.057的空泡无量纲半径公式：＝3.659＋0.847－2.0）－0.236σ－2.0）2≥2.0。空化器周围空泡采用“1/3法则”经验公式：

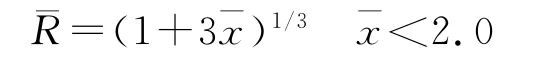
Logvinovich[2]认为，在小空泡数下超空泡无量纲直径和长度满足如下经验公式：

式中：κ＝0.9～1，空泡数适用范围为0～0.25。

利用所推导的公式，计算了σ＝0.02，v＝102.7m/s时的空泡形态，分析了空泡无量纲长度lc/Rn与空泡数的关系，如图3、图4所示，结果与经验公式吻合良好。

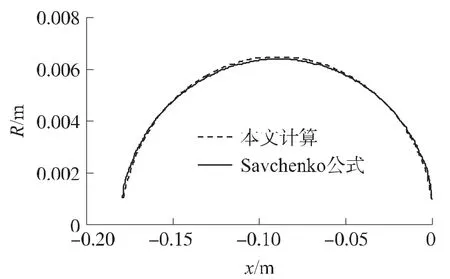
图3 σ＝0.02时的空泡形态

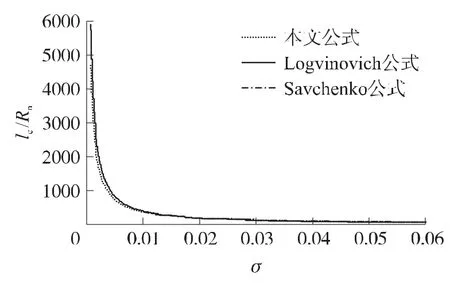
图4 空泡无量纲长度随空泡数的变化关系

图5反映了绝对时刻空泡在惯性坐标系中的形态，便于实时观察空泡随射弹运动的变化。

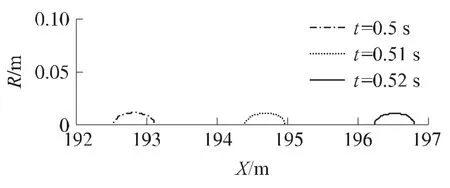
图5 不同时刻空泡在惯性坐标系下的形态

如图6所示，射弹运动过程中完整空泡扩展时间tc非常短，约10－3～10－2s；随着射弹运动时间的增加，扩展时间是减小的，且逐渐趋于平缓。

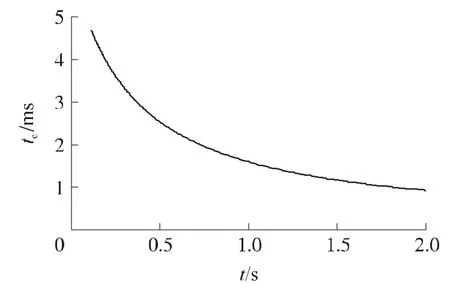
图6 完整空泡扩展时间与射弹运动时间的关系

结合算例计算可得，超空泡转变为局部空泡时σ≈0.06，射弹速度v≈60m/s。

将式（11）与“1/3”法则进行比较，如图7所示，本文公式与经验公式相比计算结果略小，这可能是由阻力系数的选取和微小量的忽略引起的。

图7 式（11）与“1/3”法则比较

4 结论

本文根据Logvinovich空泡截面独立膨胀原理、Riabouchinsky空泡闭合模型和射弹动力学方程，利用坐标变换，推导了射弹运动过程中空泡形态解析解，得到了空泡参数的计算公式，便于实时描画射弹超空泡特征；并且利用算例进行了计算分析。结论如下：

①推导公式计算结果与经验公式吻合良好，空化器周围的空泡尺寸简化计算公式所得结果比经验公式略小。

②不考虑扰动压强，自然条件下完整空泡的扩展时间仅依赖于航行体经过空泡闭合处时的参数；超空泡的最大长度取决于完整空泡扩展时间和物体运动状态。

③射弹速度越大，深度越小，首尾压差对速度影响越小；当v≥100m/s，H≤100m时，影响可以忽略；当射弹速度较小，深度较大时，需要考虑前后压差的影响。

④完整空泡扩展时间非常短，且随着射弹运动时间增大而减小，逐渐趋于平缓。

⑤空泡数为0.06，射弹速度为60m/s左右时，超空泡开始蜕化为局部空泡。

[1]SAVCHENKO Y N.Experimental investigation of supercavitating motion of bodies[J].Supercavitating Flows，2001（4）：1－30.

[2]LOGVINOVICH G V.Hydrodynamics of flow with free boundaries[M].Kiev：Naukova Dumka，1969.

[3]曹伟，王聪，魏英杰，等.自然超空泡形态特性的射弹试验研究[J].工程力学，2006，23（12）：175－179.CAO Wei，WANG Cong，WEI Ying－jie，et al.High－speed projectile experimental investigations on the characteristics of natural supercavitation[J].Engineering Mechanics，2006，23（12）：175－179.（in Chinese）

[4]孟庆昌，张志宏，刘巨斌，等.超空泡形态及其流动特性的数值模拟[J].应用力学学报，2010，27（3）：476－480.MENG Qing－chang，ZHANG Zhi－hong，LIU Ju－bin，et al.Numerical simulation of supercavity profile and flow characteristics[J].Chinese Journal of Applied Mechnics，2010，27（3）：476－480.（in Chinese）

[5]SEMENENKO V N.Dynamic processes of supercavitation and computer simulation [J].Supercavitating Flows，2001（12）：1－30.

[6]孟庆昌，张志宏，刘巨斌.海洋环境扰动对水下航行体超空泡形态的影响[J].弹道学报，2010，22（4）：31－35.MENG Qing－chang， ZHANG Zhi－hong， LIU Ju－bin.Supercavity profile of underwater vehicle influenced by environmental disturbance of ocean[J].Journal of Ballistics，2010，22（4）：31－35.（in Chinese）

[7]张学伟，张亮，王聪，等.基于Logvinovich独立膨胀原理的超空泡形态计算方法[J].兵工学报，2009，30（3）：361－365.ZHANG Xue－wei，ZHANG Liang，WANG Cong，et al.A calculation method for supercavity shape based on the Logvinovich independence principle of the cavity section expansion[J].Acta Armamentarii，2009，30（3）：361－365.（in Chinese）

[8]SAVCHENKO Y N.Supercavitation－problems and perspectives[C]//CAV2001：4th International Symposium on Cavitation.California：California Institute of Technology，2001：1－8.

[9]RAND R，PRATAP R，RAMANI D，et al.Impact dynamics of a supercavitating underwater projectile[C]//ASME Design Engineering Technical Conference.Sacramento，California：ASME，1997：1－11.

[10]VASIN A D.The principle of independence of the cavity sections expansion（Logvinovich’s principle）as the basis for investigation on cavitation flows [J ].Supercavitating Flows，2001（8）：1－27.