非均匀参数化方法在弹道优化中的应用

郭尚生，杨荣军，王良明

（1.辽沈工业集团有限公司，沈阳110045；2.中国工程物理研究院 总体工程研究所，四川 绵阳621900；3.南京理工大学 能源与动力工程学院，南京210094）

1 制导炮弹增程方案弹道优化问题

制导炮弹在进入末制导之前将沿预先设定的弹道飞行，为了使炮弹具有更远的打击能力，需要对方案弹道进行规划。预先设计的方案弹道需要考虑对炮弹运动有重要影响的重力、空气动力等因素，并且为了使炮弹在各种干扰情况下依然能够跟踪该方案弹道，需要在弹道优化时限定攻角控制量的幅值，即在规划弹道时使制导炮弹有一定的控制余量。

1.1 制导炮弹增程弹道优化性能指标函数

考虑制导炮弹的无动力增程弹道优化问题，状态变量主要包括飞行速度、弹道倾角、飞行高度和射程，控制变量取飞行中的攻角。针对增程优化的设计要求，为使射程最大化，并考虑到终端约束条件，选择的性能指标函数为

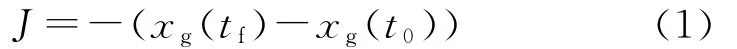
式中：t0，tf分别为优化段起始时刻、终端时刻；xg（t0），xg（tf）分别为起始时刻、终端时刻的位置射程分量。

1.2 制导炮弹的运动模型

制导炮弹的飞行弹道主要由初始条件和作用在弹上的力决定，并且描述制导炮弹运动的各状态变量是相互关联的，受到飞行力学建立的运动模型的约束。在控制系统理想的情况下，忽略弹体绕质心的短周期姿态运动过程，制导炮弹纵向平面质点弹道模型为

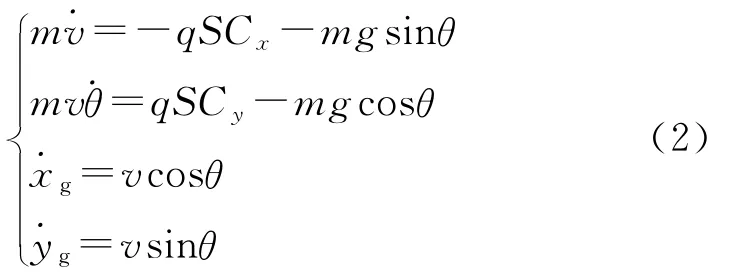
式中：m为制导炮弹质量；v为制导炮弹速度，S为弹体特征面积；θ为弹道倾角；q＝0.5ρv2，为动压；Cx，Cy分别为制导炮弹气动阻力系数和升力系数，主要与Ma和攻角α相关。在某一Ma下Cx，Cy可分别用关于攻角的二次多项式模型和线性模型近似：Cx其中：Cx0，Cx2分别为零升阻力系数和诱导阻力系数为升力系数导数。

1.3 最优控制问题描述

本质上求解满足式（2）和各种飞行状态约束的制导炮弹弹道寻优是一种动态优化问题，以攻角为控制量u（t），使下述目标函数最小：

式中：x（t）是系统的状态变量；t是时间变量；标量目标函数J（x，u，t）由终端惩罚项Φ（x（tf））和积分项L（x，u，t）构成；t0，tf分别为积分项的积分下限和上限＝f（x，u，t）是系统 状 态 方 程；c（x，u，t）是与状态、控制输入相关的等式约束函数；d（x，u，t）是与状态、控制输入相关的不等式约束函数；x（t0）＝x0是系统初始状态；Y（x（tf）），G（x（tf））分别是与状态相关的终端等式约束函数和终端不等式约束函数。

由表2可得出：在阴极极化条件下，该材料——介质体系在自腐蚀电压（-658mV）的电位下断裂寿命最长，其应力腐蚀敏感性最小、抗拉强度最大、应变量也最大。在比自腐蚀电压更正的-1 300、-1 000mV的电位下，也能激发10＃钢的应力腐蚀开裂。

2 变时间尺度的控制向量参数化

2.1 非均匀控制向量参数化

最优控制问题（OCP）式（3）所描述的是一个两点边值问题，直接求解十分困难。目前，该问题的数值求解常采用参数化方法：先将控制时域离散化为等长的时间段，然后在优化时域内对系统模型积分来消除OCP中的系统模型动态约束，转化为一般的非线性规划问题（NLP），进而采用常用的NLP方法求解[8－11]。控制向量参数化方法是利用分段函数近似连续控制作用，通常采用分段常函数的形式，即每个时间段的控制量为常值。

将固定时间区间[t0，tf]分成N个时间段，该分段方法对应有N＋1个时间节点，每段时间内的控制量为ui，i＝0，1，…，N。传统的方法是将各时间分段均匀化，即每个节点间等距，各时间段的长度为（tf－t0）/N。若考虑到分段的影响，那么应该采用非均匀的分段方法，除了初始和终端时间节点外，每个时间节点ti都需要进行优化。控制变量经参数化处理后，式（3）的最优控制问题即可转化为含有N－1个时间节点和N个控制参数的NLP问题。

引入标准化的时间变量τ，在时间段[ti，ti＋1]上定义dτ，满足条件：

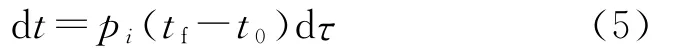
即，pi为时域[ti，ti－1]到标准化时域[τi，τi－1]的尺度因子，原控制时域[t0，tf]就转化为标准化时域[0，1]，称式（5）的变换为时间尺度变换。对式（5）积分可得到：

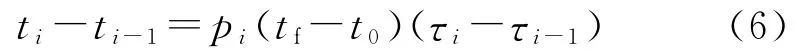
因此，每个标准化的时间段长度均为

这样就可以用传统的均匀控制向量参数法来解决非均匀参数法的问题。

定义函数：

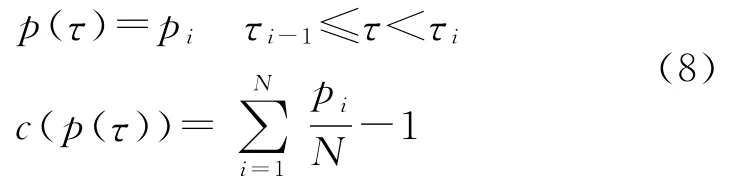
且满足约束条件则原时域[t0，tf]上的连续的无限维 OCP式（3）即转化为标准化时域[0，1]内的有限维优化问题：

式（9）中的各标准化时间节点τi是等间距的，这样每个时间子区间的状态转变为初值问题求解，可以采用均匀参数化的方法来求解。

为了有效地计算目标函数值，引入一个新变量l（τ），并 使 其 满 足＝p（tf－t0）L（x，u，τ），初值l（0）＝0。式（9）的系统微分方程、参数和初始状态已知，系统的后续状态实际上只由控制输入u（τ）确定，即x（τ）＝（ui，τ）。对 方 程＝p（tf－t0）×L（x，u，τ）和＝f（x，u，τ）在时间区间[0，1]数值积分可获得系统状态（ui，τ）和目标函数J。将描述标准化时间分段的参数pi写成向量形式p＝（p1p2…pN）T，则可取k维的控制向量ui（i＝1，2，…，N）和p作为待优化的参数，用一个kN＋N维的参数向量表示：

通过上述变换，用离散的控制量在优化时域内对系统状态方程积分，从而将动态系统模型的约束完全消去，式（9）转化成通用、易求解的有限维参数NLP问题：

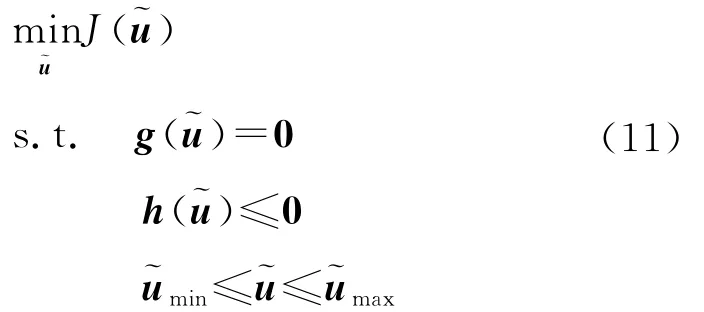
2.2 参数化的制导炮弹最大射程弹道优化问题

制导炮弹滑翔弹道优化是一个初始状态已知，但终端时刻和终端状态未知或部分未知的过程优化问题。由于制导炮弹飞行的终端时刻tf一般是未知的，这样给微分形式弹道模型的积分计算带来不便。设飞行时间ts＝tf－t0，将ts也作为待优化的参数，可将弹道优化问题转化成如下形式：

用离散化的攻角在弹道优化时域内对弹道方程积分，转化为形如式（11）的NLP问题，待优化参数为＝（α1…αNp1…pNts）T。针对转化后的NLP问题，可利用适于约束优化问题的序列二次规划方法[12]高效地求解。

3 数值仿真与分析

设某制导炮弹的基本参数、初始发射条件和约束条件：火炮炮口动能E＝1.34×107J，火箭发动机点火前的炮弹质量m0＝40 kg；火箭助推剂质量mp＝4kg，比冲I＝2 200 Ns/kg，点火时刻tp＝5s，工作时间tpw＝3s，被动段制导炮弹的质量m＝m0－mp；制导炮弹的初始发射角θ0＝55°；增程弹道优化中飞行攻角约束αmin＝－8°，αmax＝8°；终端时刻高度约束yg，tf＝2km；终端时刻的倾角约束θtf＝－20°；终端时刻的最小速度vtf＝150m/s。

按初始条件对炮弹无控段弹道解算，得到弹道顶点的时刻t0＝42.91s，飞行速度vt0＝234.35m/s，射程xg，t0＝13.140km，高度yg，t0＝11.524km。利用非均匀参数化方法与序列二次规划相结合对降弧段弹道进行优化。为便于对比观察，将增程段的弹道按时间分割为N＝25，即有25个攻角控制量参数，加上标准化的时间段参数和终端时间参数，共有2N＋1，即51个优化参数。

图1为对应于每个时间段的无量纲攻角参数，该无量纲参数乘以最大攻角幅值即为攻角。图中i的含义和式（4）相同。图2为无量纲的时间分段参数，该无量纲参数通过式（5）的时间尺度变换，即乘以参数ts/N，可得到各段的时间长度（优化的时间总长度ts＝180.18s）。通过观察时间分段参数可以看出，非均匀分段后的各时间长度是不同的，这也是与时间均匀分段的本质区别。图3（a）为无控弹道与增程弹道的对比曲线，图3（b）为对比曲线的局部放大图，图4、图5分别为无控弹道与增程弹道的速度对比曲线和弹道倾角对比曲线，图6为时间均匀分段与时间非均匀分段的攻角对比曲线。

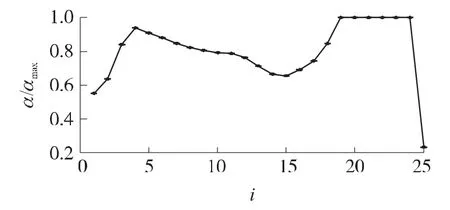
图1 无量纲的攻角参数

图2 无量纲的时间分段参数

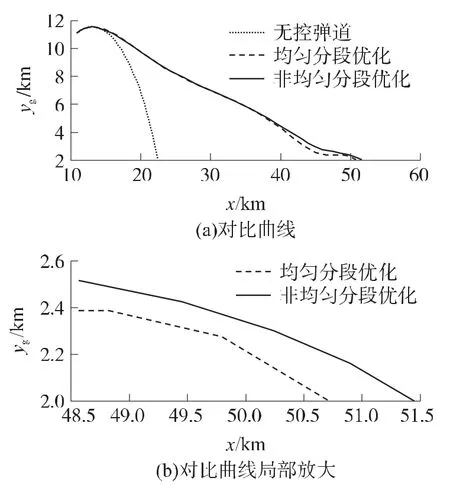
图3 无控段弹道与增程弹道对比曲线

图3显示以增程弹道优化的终端条件yg，tf＝2km为终点，无控弹道的射程为22 466.2m，时间均匀分段增程弹道优化的射程为50 721.2m，非均匀分段增程弹道优化的射程为51 450.8m。相比无控弹道，优化后的弹道可显著提高制导炮弹的射程，其中采用非均匀分段的射程比采用均匀分段的射程增加了729.6m。由图4所示的速度对比曲线看出，受到重力的作用无控弹在弹道顶点后速度会有所增大，增程优化弹道通过控制攻角产生向上的升力对重力进行一定的补偿，速度变化缓慢，并在增程弹道的末段具有一定的速度存量。采用时间均匀分段增程弹道优化的终端速度为151.2 m/s，非均匀分段增程弹道优化的终端速度为157.5 m/s，后者更加满足对终端速度的约束。图5所示增程弹道的弹道倾角幅值较小、变化较慢，相比无控弹的飞行时间也较长。时间均匀分段优化弹道的飞行时间为220.9s，非均匀分段优化弹道的飞行总时间为223.1s，终端倾角均为θtf＝－20.0°，而相比非均匀分段的增程弹道，均匀分段增程弹道的倾角波动较大，前者更利于弹道控制。图6表明时间非均匀分段优化弹道的攻角控制量在相应时刻迅速调整，可以较好地反映出攻角的变化规律。

图4 无控段弹道与增程弹道速度对比曲线

图5 无控段弹道与增程弹道倾角对比曲线

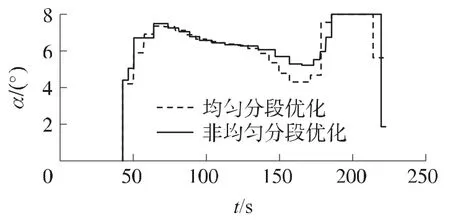
图6 均匀分段与非均匀分段攻角对比曲线

4 结束语

本文基于纵向质点弹道模型，引入了基于时间尺度变换的时间非均匀分段思想，对攻角变量参数化，将动态规划问题转化为通用的有限维NLP问题，然后利用序列二次规划方法进行求解，获得了满足各种约束的增程优化弹道。通过仿真验证了该方法的有效性，相比传统的时间均匀分段方法，非均匀分段优化的弹道射程更远、终端速度更大，且更为平滑，有利于进行弹道跟踪控制。

[1]JEPPS G.Linearised optimal control and application to a gliding projectile[C]//AIAA Atmospheric Flight Mechanics Conference.Canberrn：AIAA，1985.

[2]FLECK V.Increase of range for an artillery projectile by using the lifting force[C]//19th International Symposium on Ballistics.San Francisco：IBC，1996.

[3]BETTS J T.Survey of numerical methods for trajectory optimization[J].Journal of Guidance，Control and Dynamics，1998，21（2）：193－207.

[4]MICHAEL R I，FARIBA F.A perspective on methods for trajectory optimization [C ]//AIAA/AAS Astrodynamics Specialist Conference and Exhibit.Monterey，California：AIAA，2002.

[5]李瑜，杨志红，崔乃刚.助推－滑翔导弹弹道优化研究[J].宇航学报，2008，29（1）：66－71.LI Yu，YANG Zhi－hong，CUI Nai－gang.A study of optimal trajectory for boost－glide missile[J].Journal of Astronautics，2008，29（1）：66－67.（in Chinese）

[6]CHEN Gang，HU Ying.Optimization design on RLV reentry trajectory based on genetic algorithm [J].Journal of Solid Rocket Technology，2006，29（4）：235－238.

[7]CHEN Gang，XU Min，WANG Zi－ming，et al.RLV reentry trajectory multi－objective optimization design based on NSGA－Ⅱalgorithm.AIAA－2005－6131[R].2005.

[8]LOXTON R C，TEOA K L，REHBOCKA V.Optimal control problems with a continuous inequality constraint on the state and the control[J].Automatica，2009，45（10）：2 250－2 257.

[9]LOXTON R C，TEOA K L.Optimal control problems with multiple characteristic time points in the objective and constraints[J].Automatica，2008，44（11）：2 923－2 929.

[10]雷阳.一种求解最优控制问题的非均匀控制向量参数化方法[J].中国石油大学学报，2011，35（5）：180－184.LEI Yang.A non－uniform control vector parameterization approach for optimal control problems[J].Journal of China University of Petroleum，2011，35（5）：180－184.（in Chinese）

[11]BRIAN C，FABIEN.Some tools for the direct solution of optimal control problems[J].Advances in Engineering Software，1998，29（1）：45－61.

[12]GOH C J，TEO L K.Control parameterization：a unified approach to optimal control problems with general constraints[J].Automatica，1988，24（1）：3－18.