基于最小方差的声速测量实验数据不确定度分析尺度

徐仰彬

（西安建筑科技大学，陕西 西安 710055）

在物理实验的数据处理中，经常会通过多次测量取平均值来减少实验误差。但是在测量的过程中往往会忽略估计值对真值的影响，或者会认为测量次数越多，结果越准确。经过笔者研究发现，事实并非如此。比如在声速测量试验中，求驻波波长的时候，需要通过多次测量取平均值来逼近真值。

1 对测量数据的估计

测量波长时，需要对测量数据进行估计，因为估计是数据的函数，而数据是随机变量，估计也是随机变量，定义估计量为A，因为是对同一个物理量（波长）的多次测量。数据分布类似于带噪声的直流电平，这里我们数学建模为［2，3，4，6］：

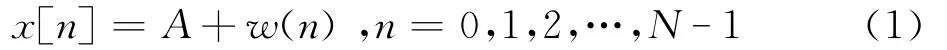
x［n］为每次的测量量，w［n］为白高斯噪声（WGN）具有均值为零，方差为σ2的高斯分布，并且所有测量数据互不相关，因为信号来源为电信号，同时误差分布均匀，所以采用WGN抽象是合理的。

对A的一个估计量可以定义为：

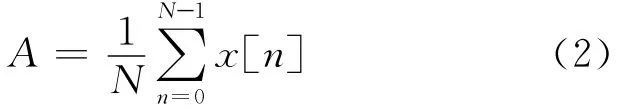
当A为无偏估计时，可以得到其概率密度函数（PDF）：

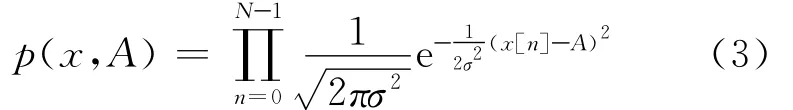
为了进一步分析各参量对结果的影响，取不同频率时的信号进行驻波法测量，来分析PDF与A之间的关系，如图1所示。

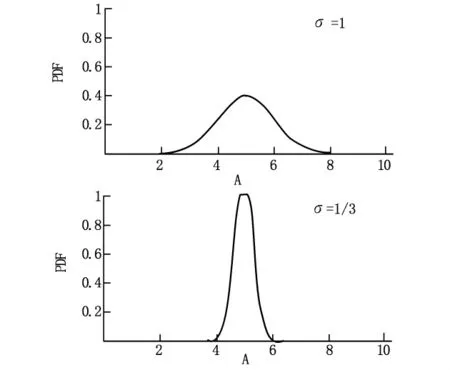
图1 σ＝1和σ＝所对应的概率密度函数

从图1中可以看出白高斯噪声的方差对结果有明显的影响，当σ2较小的时候，波长的估计值更接近于真值。从而可以得到估计量的精度是随着σ2减小而改善的。白高斯噪声主要来源于信号的产生及叠加，所以进行驻波法求波长的时候需要找到谐振点，只有在谐振的状态下才能使其方差最小。

2 实验估计值对实验误差的影响

为度量估计值的精度，我们约束偏差为零，从而求出使方差最小的估计量，对p（x；A）的对数进行求导，得到对数似然函数的曲率［1，5，7，8］。

其一阶导数为：

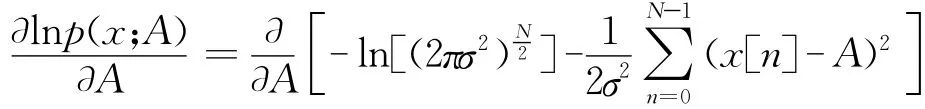
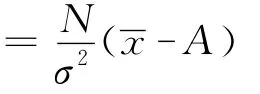
二阶导数为：

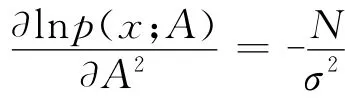
根据cramer－Bao下限定理可知：

当p（x；A）满足“正则”条件

即

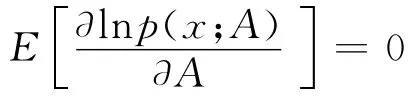
那么对任何无偏估计量A的方差必定满足

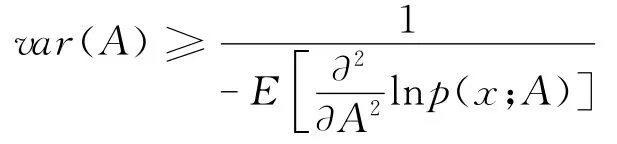
所以综合上式，可以得到：

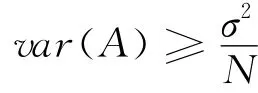
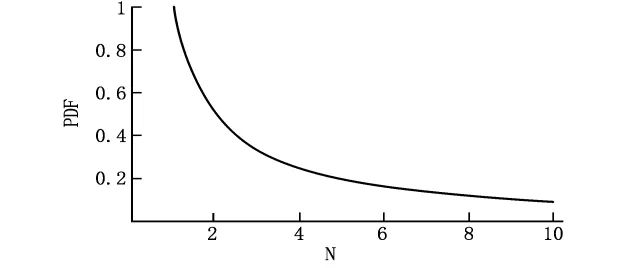
图2 方差随N的变化关系

通常由于系统误差的存在，使得估计量A会存在一定的偏差，当A为有偏估计时，定义：

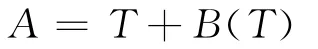
其中B（T）为估计量的偏移量，T为真值。

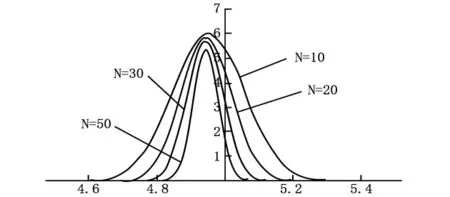
图3 测量次数与偏移量之间的关系

从图3中可以看出当存在偏移量的时候，随着测量次数的增加，真值落到估计值范围中的概率会越来越低，当达到一定的次数后，真值出现在测量值范围内的概率将趋近0，从而得到错误的结论。所以在测量的过程中并不是测量次数越多越好。

3 结 论

通过采用cramer－Bao下限定理对声速实验的实验数据不确定度进行了分析，发现并不是测量次数越多实验结果越精确，而是依赖于估计量的偏移程度，在尽量减小系统产生的误差及尽量提高信号的信噪比的情况下，测量次数保证在8～10次即可。

［1］康伟芳，薛玉春.物理实验中的不确定度及其在声速测量过程的应用［J］.大学物理实验，2006，19（1）：71－73.

［2］孙航宾，黄笃之，张禹涛.声速测量实验假象的探讨［J］.大学物理实验，2011，24（4）：51－53.

［3］郑庆华，声速测量实验的探讨［J］.大学物理，2007，26（9）.

［4］陈洁，苏建新.声速测量实验有关问题的研究［J］.物理实验，2008，28（6）：31－34.

［5］凌亚文，史彭，华中文.大学物理实验［J］.科学出版社，2006.

［6］李道夲.信号的统计检测与估计理论［J］.科学出版社，2004.

［7］孙航宾.声速测量实验假象的探讨［J］.大学物理实验，2011，08：50－52.

［8］张俊玲.驻波法测量声速实验的系统误差分析［J］.大学物理实验，2012，10：81－83.