基于DIS系统对弹簧牵动磁体振动产生电磁感应对应参量研究

施应恒，王昆林

（楚雄师范学院，云南 楚雄 675000）

将螺旋弹簧竖直固定，末端挂上一个条形永久性磁铁，形成一个准弹簧振子，使其产生振动，是一个典型的力学机械振动问题。在磁体振动行程范围内，置一个多匝漆包线线圈，磁体在螺旋弹簧牵引下上下振动时，将在线圈中产生感应电动势，从理论上讲，弹簧振子的各个参量将转换为电磁参量，并一一对应。采用DIS数字化信息测量系统对各参量进行测量，将力学机械振动参量与电磁学电磁参量进行牵连式对比研究。

1 原理及实验装置

实验装置见图1，均质螺旋弹簧的质量为ms，劲度系数为k，条形磁铁的质量为m，漆包线线圈的总匝数为N。条形磁铁上下振动时，在线圈中产生感应电动势为［2，4］：

使用DIS系统中电压传感器可探测到此量，并使其数量化和图形化。与标准的弹簧振子相比，条形磁铁还受到线圈中感应电流对它的作用力，这是一个阻碍磁铁振动的阻力，但此力十分微弱，可忽略不计。

条形磁铁在螺旋弹簧的牵引下做简谐振动，其振动方程为［1，3］：

图1 实验装置图

此二阶微分方程的解为：

即，位移x是时间t的余弦函数。

（2）、（3）式中的角频率：

其振动周期T为：

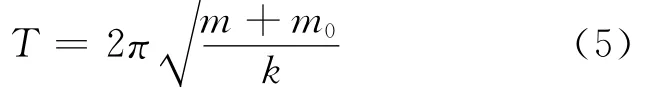
通过DIS数字化信息测量系统测量漆包线圈中的感应电动势，并使其数字化、图像化，从而可进行参量牵连比较性研究［6－7］。

2 实验研究

2.1 单根弹簧牵动条形磁体的振动研究

用一根已知弾劲系数K＝28.0 N／m，质量ms＝15.00 g的弹簧与质量m＝282.00 g的条形磁铁按照图1组装好。使弹簧牵动磁体振动起来，启动DIS系统，传感器检测到变量，数据采集器采集数据经计算机处理后，绘出图线，见图2。

图2 单根弹簧单线圈的εt图

由图2可知，线圈中的感应电动势ε与时间t成余弦关系，和（3）式是一一对应，由此可知，其弹簧振子的机械振动参量与电磁感应的参量也是一一对应的。

2.1.1 周期的牵连性研究

从图2上直接可得：T0＝0.642 53 s，两者相差ΔT＝T0T＝0.006 s，相差很小，可忽略。

2.1.2 线圈匝数对振动情况的影响

若在上述的基础上，再串联上一个线圈，使之匝数变为上述的2倍，其余器材不改变，照图1组装好。使弹簧牵动磁体振动起来，启动DIS系统，传感器检测到变量，数据采集器采集数据经计算机处理后，绘出图线，见图3。

图3 单根弹簧双线圈的εt图

由图3直接可得：T′0＝0.642 53 s，感应电动势的最大值：ε′max＝0.5 V；在图2上可得，T0＝0.642 53 s，感应电动势的最大值εmax＝0.25 V，显然，T′0＝T0，ε′max＝2εmax。

综上所述，周期的大小与线圈匝数无关，与（5）式吻合，感应电动势的最大值与线圈匝数有关，这与（1）式也是相吻合。

2.2 双根弹簧牵动条形磁体的振动研究

2.2.1 两根弹簧串联牵动条形磁铁的振动研究

用两根弾劲系数k1＝k2＝34.0 N／m，质量ms1＝ms2＝20.00 g的弹簧串联后与质量m＝282.00 g的条形磁铁按照图1组装好。使弹簧牵动磁体振动起来，启动DIS系统，传感器检测到变量，数据采集器采集数据经计算机处理后，绘出图线，见图4。

图4 两根弹簧串联的εt图

由图4可知，线圈中的感应电动势与时间t成余弦关系，和（3）式是一一对应，由此可知，其弹簧振子的机械振动参量与电磁感应的参量也是一一对应的。

2.2.2 弹簧弾劲系数的牵连性研究［5］

2.2.3 两根弹簧并联牵动条形磁铁的振动研究

用两根弾劲系数k1＝k2＝34.0 N／m，质量ms1＝ms2＝20.00 g的弹簧并联后与质量m＝282.00 g的条形磁铁按照图1组装好。使弹簧牵动磁体振动起来，启动DIS系统，传感器检测到变量，数据采集器采集数据经计算机处理后，绘出图线，见图5。

由图5可知，线圈中的感应电动势ε与时间t成余弦关系，和（3）式是一一对应，由此可知，其弹簧振子的机械振动参量与电磁感应的参量也是一一对应的。

2.2.4 弹簧弾劲系数的牵连性研究

从力学理论可知，两根弹簧并联的弾劲系数k0＝k1＋k2，k0＝68 N／m，Δk＝kk0＝1.2 N／m

图5 两根弹簧并联的εt图

3 结 论

由上可见，将弹簧做机械振动的各参量转换为电磁参量，用DIS系统进行测量，每一机械振动参量与相应的电磁参量一一对应，将对机械振动的研究转为电磁振动的研究，参数的测定更加方便准确，分析研究起来更加方便准确，同样可将这一种转换为电磁参量的方法推广到其它物理量的测量上。

［1］漆安慎，杜婵英.普通物理力学［M］.北京：高等教育出版社，2005，6.

［2］梁灿彬，秦光荣，梁竹健.普通物理电磁学［M］.北京：高等教育出版社，2004，5.

［3］樊伏云，庞捷.关于简谐振动的能量问题［J］.中州大学学报，1994（4）：23－25.

［4］王洛印，胡化凯.电磁感应定律的建立及法拉第思想的转变［J］.哈尔滨工业大学学报，2009（3）：31－33.

［5］徐滔滔.关于弹簧振子振动周期的讨论［J］.大学物理实验，1998（2）：67－69.

［6］刘莹.改进PIS装置测量物体转动时所受杆支持力的方向［J］.大学物理实验，2011（6）：31－34.

［7］刘杨.用DIS研究弹簧振子系统中的机械能守恒［J］.大学物理实验，2011（6）：76－78.