状态离散的确定性多阶段群体满意决策最优的算法

张艳娟

（三峡大学理学院，湖北宜昌 443002）

群体决策问题是一类受到普遍重视和研究的决策科学问题，它广泛应用于社会政治经济，生活各个领域.群体决策由两个以上的决策者所构成，是决策群体对一集备选方案进行评价排序后选择某方案使得群体效用最大的决策活动.有关群体决策问题的研究已经取得了丰富的研究成果.文献［1］研究了一类动态多指标决策问题，应用数学理论知识建立多目标多阶段动态决策模型.通过引入一种效用函数，并据此将具有不同量纲、不同物理含义、不同指标类型的决策矩阵归一化转换到相应的效用矩阵，提高了分辨精度，物理概念更加清晰.文献［2］针对状态离散的确定性多阶段群体决策问题，建立多阶段群体决策模型，通过引入偏好关系，得到了各阶段的子过程群体满意策略以及全过程群体满意策略，提出了一种多阶段群体决策问题的逆向递推算法.文献［3］讨论了多阶段群体满意决策问题，提出了一种多阶段群体满意策略问题的最优算法，该算法的主要思想是应用图论知识将此问题转化为在多部有向赋权图中求一条权和最长的路.这些文章为群体决策问题的研究提供了很多有用的方法和理论.

本文将针对状态离散的确定性多阶段群体决策问题，利用图论的知识，将群体决策问题的多阶段与图的边集、点集对应起来，建立群体决策问题的模型一多部赋权图，定义权w 为决策者对决策的评价值或效用值，路P 的长度为P 中各边的权和，将多阶段群体满意决策问题转换成在多部赋权图中找一条最长路径的问题.依据一条最长路径上的任意两个不相邻的顶点之间是不可以被由不在这一条路径上的两个顶点组成的更长的路所替代这一事实，提出了一种多部赋权图最长路径的算法.

1 多阶段群体决策模型

定义1 设G＝（V（G），E（G），w（G））一个赋权图，其中V（G）是顶点集，E（G）是边集，w（G）是权集，如果G 满足以下条件：

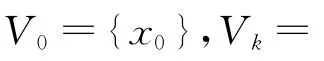
对于在连通图中寻找最长路径的问题，国内外许多学者已经做了比较多的研究.文献［4］介绍了一种比较简单通用的寻找近似最长路径的算法.文献［5］讨论了现有求解最长路径问题的几种算法，包括近似算法、参数化算法和特殊图的多项式时间算法，着重分析和比较了参数化算法中利用着色、分治和代数法研究κ－Path问题的最新结果，并提出了该问题的进一步研究方向.文献［6］通过定义一种有向图，提出了一种有向图从始点到其它任一顶点之间最长路的算法.文献［7］研究了无向连通图指定起点和终点的条件下，通过对深度优先生成树的某条路径不断地进行顶点插入的策略来获得一条近似最长路径.本文在总结和借鉴已有算法的基础上，依据一条最长路径上的任意两个不相邻的顶点之间不可以被由不在这一条路径上的两个顶点组成的更长路所替代这一事实，提出了一种多部赋权图中寻求最长路径的算法.

2 算 法

设P＝x0x1…xN是多部赋权连通图G 中连接点x0和xN的路，其中x0∈V0，x1∈V1，…，xN∈VN.设G1，G2，…，（Gm）（m≥0）为由不在路P 上的顶点组成的图G 的连通子图.

定义3 路P 中的任意两个不相邻顶点xk和xt同时分别与任意一个连通子图Gl中的顶点xp和xq（xp和xq为Gl中的点）相连接.在P 中顶点xk和xl之间路P1的长度为L（P1），在Gl中顶点xp和xq之间最长路P2的长度为L（P2），如果L（P2）＋w（xk，xp）＋w（xt＋xq）＜L（P1），即在路P 中任意不相邻两个顶点之间的路不可被由不在路P 上顶点组成的更长路所代替，则称满足这个条件的路为不可替代路.

定理1 如果路P 上的任意两个不相邻的顶点之间的路均为不可替代路，则路P 就是最长路径.

显然，如果路P 不满足上面的性质，则路P 不是最长路径.对于任意一条路P＝x0x1…xN，设点xk和xt是路P 上任意两个不相邻的顶点，连接点xk和xl之间路P1的长度为L（P1）.Gl为某个由不在路P 上的顶点所构成的图G 的极大连通子图，设xp和xq为Gl中的点，且边（xk，xp）∈E（G），（xt，xq）∈E（G）.Gl中顶点xp和xq之间最长路P2的长度为L（P2），如果L（P2）＋w（xk，xp）＋w（xt，xq）＞L（P1），则在路P上用顶点xp和xq之间的路径替代顶点xk＋1和xt－1之间的路径.因此在多部有向赋权图中寻找最长路径问题的关键是要寻找不可替代路.

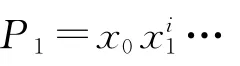
步骤4：若可被替代的点的列表为空，转步骤8，否则取出可被替代的点的列表中的点，完成一次操作以后，如果可被替代的点的列表中的点没有被替代，将其保留.否则将其删除.

步骤5：若可替代的点列表为空，转步骤8，否则遍历可以替代的点的列表，查找可替代点列表中的点，若找到可替代点列表中的点，执行步骤6，否则转步骤4.

步骤6：用可替代的点的列表中的点替代可被替代的点的列表中的点，可以得到一条新的路径，如果新路径的长度大于原来路径的长度，则可被替代的点的列表中的点将会被可替代的点的列表中的点所替代，执行步骤7.否则可被替代的点的列表中的点将不会被替代，转步骤4.

步骤7：将替代到原来选取的路径中的点加入到可被替代的点的列表中，返回步骤4，调整可被替代的点的列表.

例：在图1中，找一条从顶点x0到x4的长度最长的路径.

图1 例图

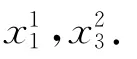
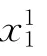
3 算法应用

在群体决策问题中，经常要对状态离散的确定性多阶段决策的群体满意策略做出判断，下面的这个例子就是实际生活中会经常遇到的.设由5个决策者构成的决策群体共同参与一个包含4个决策阶段的状态离散的确定性动态决策过程，多个决策者的权重在各个决策状态下是不变的，即决策者的权重向量为（0.1，0.3，0.3，0.1，0.2），各阶段的状态转移过程以及决策者对方案的评价值如图2所示，求全过程的群体满意策略.为了便于表述，将其策略用所经过的多个状态点来表示.

图2 状态离散的确定性多阶段决策的群体问题的示例图

步骤1：建立状态离散的确定性多阶段决策的群体满意决策问题的模型，利用在多阶段群体决策模型中计算权的方法详细计算出图2中每条边的权.比如w（x0，x）＝3×0.1＋3×0.3＋4×0.3＋7×0.1＋9×0.2＝4.9，依次计算出所有的权.此时图2就可以转化成多部赋权图，如图3所示.

图3 多部赋权图

4 结 语

近几年来，经过研究者们的努力，最长路径问题的研究取得了重大的进展，大量的文献都在研究该问题的参数化算法.本文针对生活中常见的状态离散的确定性多阶段群体满意策略问题，应用图论的知识建立了多阶段群体决策问题的模型，并在此基础上给出了算法，但是，由于该算法采用的是点逐步被替代的方式，因此计算量较大，有待进一步改善.

［1］ 戴文站，邹立华，王建章.一种基于奖优罚劣原则的多阶段多目标决策模型［J］.系统工程理论与实践，2000，6（1）：32－36.

［2］ 彭 怡，胡 杨.状态离散的确定性多阶段群决策的满意策略性［J］.运筹学学报案，2006，10（1）：80－86.

［3］ 郑文婷，刘红美，余 真.多阶段群体满意决策最优算法［J］.数学的实践与认识，2008，38（16）：44－48.

［4］ Karger D，Motwani R，Ramkmmar G D.On Approximating the Longest Path in a Graph［J］.Algorithmica，1997，18（1）：82－98.

［5］ 王建新，杨志彪，陈建二.最长路径研究问题进展［J］.计算机科学，2009，36（12）：1－4，31.

［6］ 屈芝莲.一种有向图最长路的算法、灵敏度分析及其应用［J］.科学技术与工程，2011，11（16）：3746－3449.

［7］ 孙承山，何援军，蔡鸿明.无向连通图求约束条件下近似最长路算法［J］.计算机仿真，2004，21（7）：45－47，81.