基于FPGA 的浮点与整型数据混合运算实现*

陈 坤，唐小琦，宋 宝

(华中科技大学 机械科学与工程学院，武汉 430074)

0 引言

随着FPGA 向高速，大容量，高集成度和低功耗方向的快速发展，相应的EDA 软件工具也日趋完善，提供了更多的数字信号处理IP 核，使得FPGA 在高速数字信号处理领域得到越来越广泛的应用［2］。

在FPGA 中对不同格式的数据进行运算时消耗的资源是不一样的，合理转换数据的格式可以有效地降低资源的消耗，提高运算速度［3］。对于浮点数和整型数据，如果能在不同的地方运用不同的格式，可以用最少的资源和最快的速度实现相同的功能［4］。目前有很多基于FPGA 的浮点数转换成整型数据的研究和设计，但浮点和整型数据的混合运算却未见报道。本文在研究浮点数和整型数据存储结构的基础上提出了一种浮点数和整型数据相互转换的方法，改进了一般浮点数运算中消耗资源较多和运算速度较慢的问题。

1 IEEE 754 浮点数标准

目前大多数高级语言(包括C)都是按照IEEE 754 的标准来规定浮点数的存储格式［5］。IEEE 754用科学计数法以底数为2 的小数来表示浮点数，存储格式分为三个部分:符号位(S)、指数位(E)和尾数位(M)。双精度浮点数为8 字节，包含1 位符号位，11 位指数位和52 位尾数位;单精度浮点数为4字节，包含1 位符号位，8 位指数位和23 位尾数位，如图1 所示。本文将重点分析单精度浮点数和32 位整型数据的混合运算［6］。

图1 IEEE 754 单精度浮点数格式

单精度的指数使用正偏正值形式表示，偏移值为127，指数值减去偏正值即为实际的指数大小。指数值范围为0 ～255，实际指数值范围为－127 ～128。当指数为0 时且尾数不为0 时，则浮点数A = (－1)S×21－127×0. M，称为非规格化数;若指数和尾数都为0时，则表示的浮点数为0。若指数为255，尾数部分不为0 时，则表示的为非数值;若尾数部分也为0，则表示无穷大。尾数部分为23 位，为了尾数部分能表示更多一位的有效值，IEEE754 采用隐含尾数最高数位1(即这一位1 不表示出来)的方法，因此尾数实际上是24 位，但应注意隐含的1 是一位整数(即位权位20)，在浮点格式中表示出来的23 位尾数是纯小数并用原码表示，尾数真值为:1 +尾数。即浮点数A =(－1)S×2E－127×1.M。

如01001110111100000111001111111110，符号位为0，即 为 正 数，指 数 为“10011101”，底 数 为“11100000111001111111110”。表示成二进制数即为1.11100000111001111111110 ×2157－127。

2 算法原理及推导过程

32 位有符号整数表示范围为－ 2147483647 ～2147483647，32 位单精度浮点数表示范围为3.4 ×10－38～3.4 ×1038，所以整数转浮点数时不用担心会溢出，但当单精度浮点数表示范围超过整形数据表示范围时，则会溢出，本算法设置了溢出标志位，用以表示是否溢出。

2.1 整型转换成浮点数

整型数据转换成浮点数只需求出浮点数的符号位S、指数位E、尾数位M。所求浮点数符号位与整形数据符号位相同。根据单精度浮点数的表示方法，隐含尾数最高位为1，且为整数，所以从第31 位开始检测，检测到1 时停止，并计其位于第几位，其后的位数即为指数实际值，偏置后即可得指数位;其后的数值即为所求的尾数位。

例如，整型数据为00011000101010111101000010111001，为1 的最高位位于第29 位，将整型数据规整为1.1000101010111101000010111001 ×228，可计算出浮点数的指数部分E =28 +127 =155(10011011);由于尾数部分只有23 位，这里尾数位剩下28 位，故需对剩下5 位做舍入处理。在IEEE 754 标准中，舍入处理提供了4 中可选方法:就进舍入、朝0 舍入、朝+∞舍入和朝－∞舍入。这里采用就近舍入的方法，就近舍入的实质就是通常所说的“四舍五入”。例如:尾数超过规定的23 位的多余数字是10100，多余位的值超过规定的最低有效值的一半，故最低有效位应增1，若多余的5 位是01111，则简单的截尾即可，对多余的5 位10000这种特殊情况:若最低有效位为0，则截尾;若最低有效位现为1，则向上进一位使其变为0。所以此例中要将最低有效位加1，使其变为0，得到尾数位M =10001010101111010000110。若剩下位数小于23 位，则低位补0［7］。

2.2 浮点数转换成整型

浮点数的符号位直接赋值给整数的符号位。取出浮点数中的指数值，根据浮点数的表示方法，减去偏置值后得到实际指数值n。然后从浮点数的尾数最高位开始，依次取出n 位，注意浮点表示法中隐含的尾数的最高位1，即实际整数为(n +1)位。若n≤23，则浮点数尾数部分中还有小数部分，这里采取四舍五入的方法舍去小数部分，若尾数部分取出高n 位后的最高位为1，则整数需加1;若为0，则保持不变。若n ＞23，则低位补0［8］。

例如浮点数为11001101110001010101111010000101，符号位S =1，指数位E =10011011(155)，尾数位M =10001010101111010000101。所求整型数据的符号位也为1，数 据 位 为N = 1. 10001010101111010000101 ×2155－127=11000101010111101000010100000。

3 FPGA 中算法的实现及仿真分析

考虑到实际应用中，数值在很多情况下都是从串口获得，并表现为ASCⅡ，故首先应将ASCⅡ形式的数据转换成相应进制的形式。转换过程中采用标志位来判断是整型转浮点还是浮点转整型。实现流程图如图2 所示。

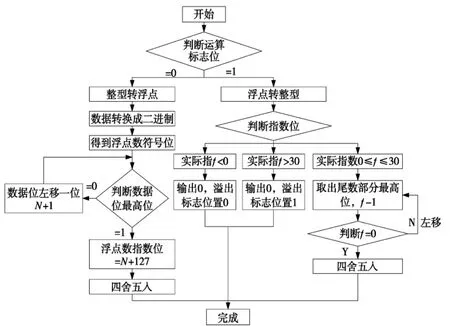
图2 转换流程图

首先判断运算标志位，裁定进行何种运算。为0则进行整型转浮点运算，为1 则进行浮点转整型运算。整型转浮点运算中，主要运用for 循环和左移操作来计算出浮点数的指数位和尾数位［1］。由于不用考虑溢出问题，故32 位整数都可转换成相应的浮点数。反之，在浮点转整型运算过程中，就需要考虑到溢出问题，故设置溢出标志位，若溢出则置1，无溢出置0［9］。整数数据部分的计算同样主要是运用VHDL 语言中的for循环和移位操作，最后也需进行四舍五入处理［10］。

4 仿真分析及实验验证

4.1 仿真分析

采用altera 公司的EP2C8Q208C8 作为测试平台，开发工具为quartus ⅡVersion9.0。工程编译完成后，耗费资源如图3 所示。工作频率为50MHz。

图3 算法消耗的资源

图4 整型转换浮点数时序图

图5 浮点数转换整型时序图

图6 三次样条插补算法计算流程

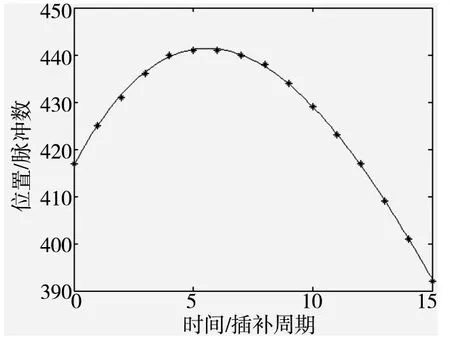
图7 理论曲线与实际插补轨迹对比

首先利用quartus 内置的在线调试工具signaltap捕获和显示实时信号。整型数据转换成浮点数的时序图如图4 所示。

如图4 所示，当标志位dir 为0 时，进行整型转浮点的运算。如输入数据为X”7839FF6B”时，实际转换结果应为X”4EF073FF”，从仿真软件可验证结果的正确性。另外从仿真软件可以看出，转换过程可在一个时钟周期(即20ns)内完成，具有很高的实时性。

浮点数转换成整型的时序图如图5 所示。当标志位为1 时，进行浮点转整型的运算。如输入数据为X”4C2A2AD5”时，实际转换理论结果应为 X”02A8AB54”，从仿真软件可以看出实际结果与理论结果一致，并且 OV 为0，表示未溢出;当输入”E38FD6AA”时，超出转换范围，故输出X”80000000”，溢出标志位OV 置1。另外转换过程也是在一个始终周期内完成。

4.2 实验验证

通过将该算法运用到一种三次B 样条曲线插补中来验证。插补过程如图6 所示。

通常，三次B 样条曲线的方程为f(t)=R0t3+R1t2+R2t+R3，式中t∈［0，1］为无纲量参数。为了计算曲线参数R0、R1、R2该算法将插补过程分为精插补和粗插补两部分。在FPGA 中整型的乘加运算可以在一个周期内完成，将计算分成整型和浮点两个部分可以有效的提高计算速度，消除在浮点计算过程中的精度丢失。

将该算法下载到FPGA 中，插补完成的数据和拟合曲线如图7 所示。

下面给出三次B 样条插补在ARM 和FPGA 中实现的速度比较。测试环境为:ARM 为920T ARM 处理器，频率为300MHz;FPGA 为EP2C8Q208C8，频率为50MHz。实验结果表明FPGA 中数据处理的效率远高于在ARM 中，结果如表1 所示。

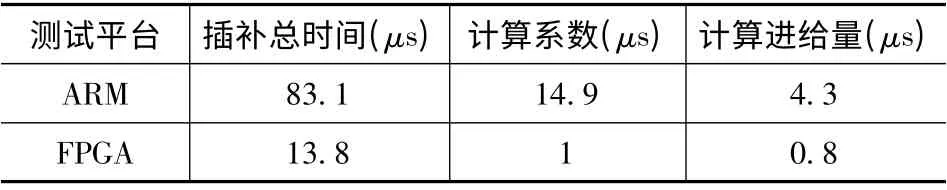
表1 三次样条插补算法在ARM 和FPGA 中实现的速度比较

5 结束语

本文采用Quartus 软件平台，选用Altera 公司的EP2C8Q208C8 芯片，采用VHDL 硬件描述语言，对算法进行了功能仿真验证和实验验证。从实验结果看，能实现32 位整数与单精度浮点数之间的相互转换;在系统时钟为50MHz 的情况下，转换所用时间约为0.02μs，完全可以满足非特殊情况下的高速数字信号处理。本文算法可以很容易的根据实际整数的范围和精度进行调整，并且可以推广到其他浮点格式，可通过合理的转换数据格式有效地提高数据处理速度和减少所占资源。

［1］姜雪松，刘东升. 硬件描述语言VHDL 教程［M］. 西安:西安交通大学出版社，2004.

［2］王红，彭亮，于宗光. FPGA 现状与发展趋势［J］. 电子与封装，2007(7):32－37.

［3］李宏钧，胡小龙. 流水线的FPGA 低功耗设计［J］. 计算机系统应用，2010，19(8):234－237.

［4］张小新，魏厚龙. FPGA 技术及开发方式概述［J］. 山西电子技术，2008(5):86－87.

［5］周磊，成开友，孙宏国. 单精度浮点数到十进制数转换的IP 核设计［J］. 盐城工学院学报，2011(1):56－60.

［6］WAHAN W. IEEE Standard 754 for binary floating-point arithmetic. Lecture Notes on the status of IEEE 754［P］.1997－10－01.

［7］唐小明，张涛，王贞杰. 一种新的基于FPGA 的数据格式转换方法［J］. 现代电子技术，2011(8):110－112.

［8］王元良，李允俊. 基于ARM 的浮点数转换成整数的改进算法［J］. 信息技术，2007(12):18－19.

［9］韩进，程勇，齐现英. VHDL 在数字集成电路中的应用［J］. 山东科技大学学报，2003，22(4):74－77.

［10］张小妍，邵杰. 高速浮点单元的FPGA 实现［J］. 信息化研究，2009，35(11):24－27.