基于微分进化算法的平面度误差评定*

王东霞，温秀兰，汪凤林

(南京工程学院 自动化学院，南京 211167)

0 引言

平面是构成实体零件的最重要几何元素之一，它不仅是众多测量的基准面，而且也是构成许多机械产品工作台的基本要素，如机床的平面导轨、工作台等，而且常作为检测的基准面［1-2］，平面度误差的大小对产品的质量及寿命至关重要，因此对平面度误差进行高效准确的评定具有重要的实用价值。在当前的工业实践中，平面度误差的评定遵循几何公差的表示与解释标准。美国国家标准协会(ANSI)尺寸与公差标准Y14.5［3］提出形状误差评定必须参考一个理想的几何特征。ISO 标准［4］建议形状误差的评定应基于最小区域的概念。平面度误差被定义为在两平行平面之间包含所有测量点的距离最小值。虽然最小二乘法是几何误差评定的最广泛应用的方法之一，它容易实现、计算高效，常常被应用在坐标测量机中。但是，最小二乘法不能满足最小区域条件，不符合ISO 标准，容易导致形状误差的过估计和好工件的废弃。

为了获得最小区域解，多年来一直有学者致力于这方面的研究。Murthy and Abdin［5］提出了一种简单搜索技术。Fukuda and Shimokohbe［6］应用极大极小近似方法寻求最小区域解，Wang［7］，Kanada 和Suzuki［8］应用了统一线性逼近技术实现最小区域解。Hermann［9］提出借助计算几何方法求解平面度误差。求解平面度误差评定最小区域解是属于非凸问题，可以被表述成非线性优化问题，因此评定方法实际上是优化问题。近年来有不少学者提出了智能计算方法实现最小区域解计算。智能计算如遗传算法［10-12］、混合优化算法［13］、粒子群优化算法［14］、进化策略［15］、改进蜂群算法［16］等被用于平面度误差的评定。但是，若系统需多个参数需要同步优化，遗传算法存在早熟、参数依赖性强的缺点，粒子群算法容易陷入局部最优，限制了其应用。而微分进化算法以其在多参数非线性优化方面的优越性能在1996 年日本召开的第一届国际进化优化计算竞赛(ICEO)中取得了优异成绩，受到了越来越多的重视［17］，已经在电力、空间、控制、经济等领域得到应用。鉴于微分进化是一种解决非凸及非线性优化问题的有效的智能算法，具有简单灵活、效率高、搜索能力强、鲁棒性好、控制参数少等特点，本文提出了一种基于种群优化的微分进化算法，并将其应用于平面度误差最小区域解计算。

1 平面度评定的数学模型

假定点Pi(xi，yi，zi)(i=1，2，…，n)是被测平面上的测量点，其中n 为测量点数，按最小区域法评定平面度误差实际上是寻找包容被测实际平面且距离最短的两理想平行平面，因此属于求最小化问题。假设最小区域法的两平行平面其中之一的平面度公式为:

平面上的测量点Pi(xi，yi，zi)到平行平面的距离公式为:

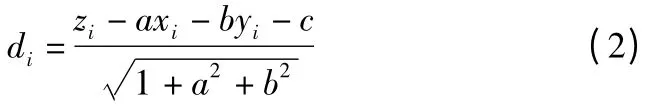
则两平行平面间的最小距离为:

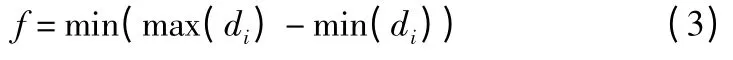
可以明显看出，最小距离f 是参数a，b 的函数。所以，求解最小区域平面度误差转变为搜索a，b 的值，直到距离函数f(a，b)的值最小，则最小值即为平面度误差。这是一个非线性优化问题。

2 微分进化算法

2.1 变异操作

初始化完成以后，微分进化利用变异策略产生一个与每个个体Xi，G相关的变异向量Vi，G，即当前种群的目标向量。有5 种最常用的变异策略“DE/rand/1”，“DE/best/1”，“DE/rand-to-best/1”，“DE/best/2”，“DE/rand/2”。变异策略中包含参数变异因子，F∈(0，1)，用于控制变异的幅度，即差值的放大倍数。

2.2 交叉操作

变异操作完成后，为了维持种群个体的多样性，交叉操作应用到每对目标向量和它的相应变异向量产生一个测试向量Ui，G=(，，…，)在基本微分进化中，微分进化交叉操作定义为:

在公式(4)中，交叉因子CR 是一个指定的常数，交叉算子并且是介于0 和1 之间的连续实数。如果CR 的值较大，DE 的收敛速度会加快;如果CR 的值较小，DE 的鲁棒性会更好，但是会增加问题的执行时间［20］。

2.3 选择操作

新一代个体的产生方式为:

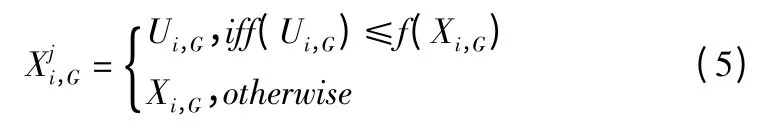
式中，f()为待优化的目标函数。

在此过程中如果新产生的子代个体的适应度比父代大，即子代个体更优良，那么Ui，G将取代其相应的父代个体进入种群，参与下一代的进化。选择操作保证了在进化过程中种群不发生退化现象并且能够维持种群规模。

3 实例

在我们的研究中，选择变异策略“DE/best/1”，参数设置为D=2;种群大小NP =10* D，变异因子F =0.85，交叉因子CR=0.9，进化代数设置为100 代。为比较验证算法的可行性，选择3 个典型的例子。

3.1 平面度测量数据

为了对比，取文献［11］平面度采样数据，应用微分进化算法进行平面度误差评定，结果列于表1 中。从表1 中可以看出，平面度误差的最小二乘(LSC)评定结果、标准遗传算法评定结果(EGA)和改进遗传算法(IGA)［11］的 评 定 结 果 分 别 为0.0219，0.2161 和0.01839。而微分进化的评定结果为0.01838，与文献［11］有着很好的一致性。

表1 数据评定结果(mm)

3.2 平面度测量数据

平面度采样数据取自文献［8］，微分进化评定结果列于表2 中，从表2 中可以看出，平面度误差的最小二乘(LSC)评定结果、标准遗传算法评定结果(EGA)和文献［8］的评定结果分别为0.00303，0.002739 和0.002627。而微分进化的评定结果为0.002627，与文献［8］有着很好的一致性。

表2 数据评定结果(mm)

在标准遗传算法(EGA)中，种群大小设置为40，交叉变异因子分别设为0.90 和0.20，最大代数为200，由图1 和图2 可以看出，微分进化算法结果更精确稳定。在大约进化至40 代时已达到稳定值。

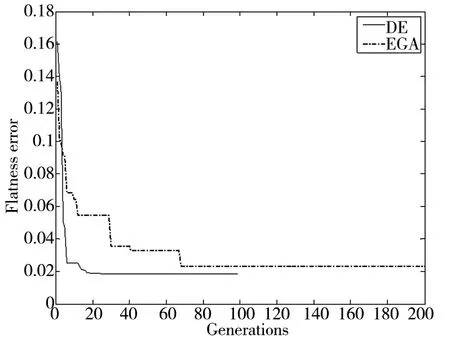
图1 DE 与EGA 对于文献［11］中测量数据的优化过程

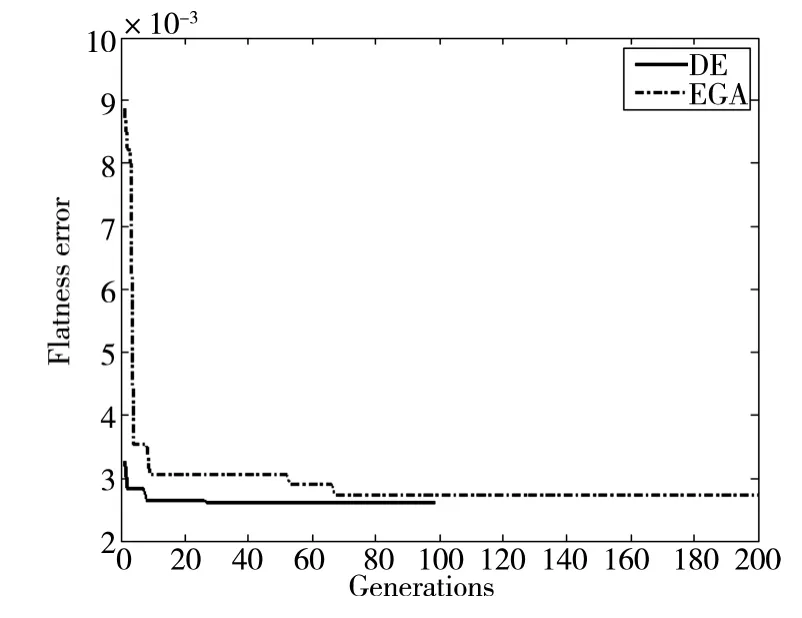
图2 DE 与EGA 对于文献［8］中测量数据的优化过程

3.3 采样数据

取文献［16］平面度采样数据，应用微分进化算法进行平面度误差评定，结果列于表3 中。单次运行结果如图3 所示。运用微分进化算法对该例独立运行30 次，DE 算法求得最优目标函数值的平均值为0.15487，标准差为9.12314E-11，完成100 代进化所需的时间是0.38s。计算结果与文献［15］、文献［16］的结果相比较，从表3 中可以看出，文献［16］中所提出的算法与微分算法的平面度误差计算结果相同，从时间和误差标准差的结果来看，微分进化方法结果更稳定，花费时间更少。由上比较结果可见，微分进化算法不仅能收敛到全局最优解，而且具有较快的收敛速度，从计算精度、稳定性和优化效率等方面综合考虑优于其他算法。

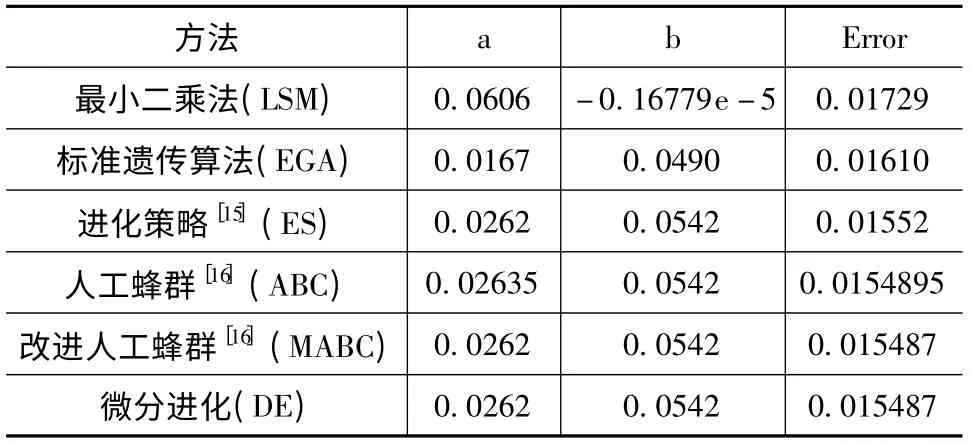
表3 不同算法计算的比较(mm)

图3 微分进化算法对文献［16］中的测量数据的优化过程

4 结论

本文结合平面度误差的评定特点，提出了一种有效的实现最小区域平面度误差评定的微分进化算法，与以往的平面度评定算法相比，具有简单、灵活、高稳定性、快速收敛性和更高的计算精度等优点，大量实例验证了提出的算法能够有效地搜索到全局优化结果，适宜于对高精度平板进行快速精密测量。

［1］史立新，朱思洪. 基于matlab 的平面度误差最小区域法评定［J］. 组合机床与自动化加工技术，2005(9):58－59.

［2］刘永超，陈明. 形位误差的进化算法［J］. 计量学报，2001，22(1):18－21.

［3］ANSI Standard Y14.5. Dimensioning and tolerancing. New York［S］:The American Society of Engineers，1982.

［4］ Technical Drawings—Geometrical Tolerancing［S］. ISO/R1101，1983.

［5］Murthy TSR，AbdinSZ. Minimum zone evaluation of surfaces. International Journal of Machine Tools Design and Research.1980(20):123－36.

［6］Fukuda M，Shimokohbe A. Algorithms for form error evaluation-methods of minimum zone and the least squares［C］.In Proceedings of the International Symposium on Metrology and Quality Control in Production. Tokyo. 1984:197－202.

［7］Y. Wang. Minimum zone evaluation of form tolerances［J］.Manufacturing Review. 1992，5(3):213－220.

［8］T. Kanada，S.Suzuki. Evaluation of minimum zone flatness by means of non-linear optimization technique and its verification［J］.Precision Engineering. 1993，15(2):93－99.

［9］Hermann G. Robust convex hull-based algorithm for straightness and flatness determination in coordinate measuring［J］.Acta Poly technica Hungarica.2007(4):111－20.

［10］Hsien-Yu Tseng. A genetic algorithm for assessing flatness in automated manufacturing systems［J］. Journal of Intelligent Manufacturing.2006，17(3):301－306.

［11］Xiu-Lan Wen，Xiao-Chun Zhu，Yi-Bing Zhao，et al. Flatness error evaluation and verification based on new generation geometrical product specification (GPS)［J］. Precision Engineering. 2012(36):70－76.

［12］温秀兰，宋爱国. 改进遗传算法及其在平面度误差评定中的应用［J］. 应用科学学报，2003，21(3):221－224.

［13］Ke Zhang. Study on Minimum Zone Evaluation of Flatness Errors Based on a Hybrid Chaos Optimization Algorithm［C］. Lecture Notes in Computer Science. Emerging Intelligent Computing Technology and Applications，2009(5754):193－200.

［14］YU Xiao，HUANG Mei fa. Flatness Error Evaluation of the New Generation of GPS Based on an Improved Particle Swarm Optimization［J］. MICROELECTR-ONICS ＆ COMPUTER. 2010，27(4):50－53.

［15］温秀兰，赵茜. 基于进化策略的平面度误差评定［J］. 仪器仪表学报，2007，28(5):832－836.

［16］罗钧，王强，付丽. 改进蜂群算法在平面度误差评定中的应用［J］. 光学精密工程，2012，20(2):421－430.

［17］刘棕成，董新民，陈勇. 基于微分进化算法的二自由度PID 控制器参数优化［J］. 飞行力学，2012，30(2):139－146.

［18］Stron Rand Price K. Differential evolution—a simple and efficient heuristic for global optimization over continuous spaces［J］. Journal of Global Optimization. 1997(11):341－359.

［19］江家宝，尤振燕，孙俊. 基于微分进化算法的多阶段投资组合优化［J］. 计算机工程与应用，2007，43(3):189－193.

［20］刘长良，于明. 微分进化算法研究及其在热工过程参数辨识中的应用［J］. 化工自动化及仪表，2011，38(3):269－273.