Stewart 型并联机构的振动建模与分析*

孙国立，杨晓钧

(哈尔滨工业大学 机电学院，哈尔滨 150001)

0 引言

并联运动机床是Stewart 型并联机构在现代工业中的一个重要应用领域。为实现并联机床较好的加工精度、运动性能以及保证其较高的控制精度，Stewart 型并联机构振动特性的研究就显得格外重要。Gosselin［1］研究了并联机构动平台与各个支链之间的刚度映射关系。Miller 等人［2］运用拉格朗日法建立了Stewart 机构闭环形式的动力学方程。J. Wang 等人［3］以及B. Dasgupta 等人［4］分别运用牛顿欧拉法和虚功原理建立了机构的动力学方程。Chen［5］研究了并联机构的刚度特性及其稳定性。Seling 和Ding［6］在将液压缸看作弹簧阻尼系统并且假设各支链无阻尼的前提下，得到了Stewart 平台的线性方程，用以研究机构的振动特性。Kim［7］提出了一种被动控制策略，主要应用于Stewart 平台的运动误差控制。Cheng 等人［8］给出了Gough-Stewart 平台的多体系统模型来进行振动控制，以减少风对电波望远镜的干扰。然而，这些振动模型应用于控制算法设计中都太过简化，不适合对并联机构进行较为精确的振动分析与控制。在本文中，首先对Stewart 型并联机构进行了运动学分析，之后建立了该机构的振动动力学模型，最后对其振动特性进行研究，得出了该机构固有频率的变化特性。

1 并联机构的运动学

Stewart 型并联机构主要由动平台、定平台和驱动杆组成，如图1 所示。上平台为定平台，与机床床身固定在一起。下平台为动平台，即加工平台，铣刀及夹具固定于动平台的中心处。动平台与定平台之间通过可以伸缩的驱动杆来连接，其中动平台与驱动杆通过球铰连接，定平台和驱动杆通过万向节连接。通过调节各个驱动杆的长度，动平台可以实现不同的位置和姿态。

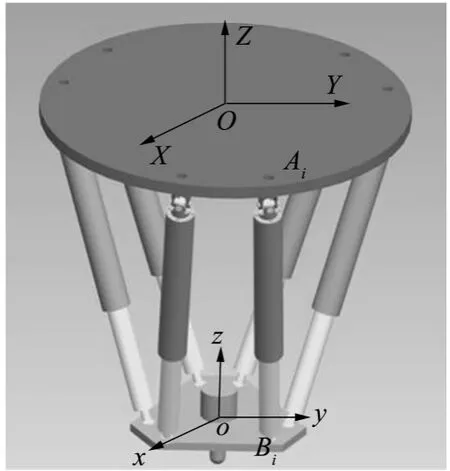
图1 并联机构结构简图

此并联机床有六个自由度，包括三个线性平移自由度和三个转动自由度。在研究并联机床两平台之间的位姿关系时，建立了两套坐标系，他们分别是定坐标系(也叫参考坐标系)和动坐标系。定坐标系O-XYZ 用A 来表示，固定于定平台上。动坐标系o-xyz用B 来表示，固定于动平台的中心上，随着动平台一起运动，如图1 所示。

动平台在参考系中的位置可以用向量p =(X，Y，Z)来表示，即动坐标系原点o 在参考坐标系中的位置坐标。动坐标系相对于定坐标系的姿态可以用旋转矩阵ABRzxz来表示。旋转矩阵可以通过欧拉角求得:

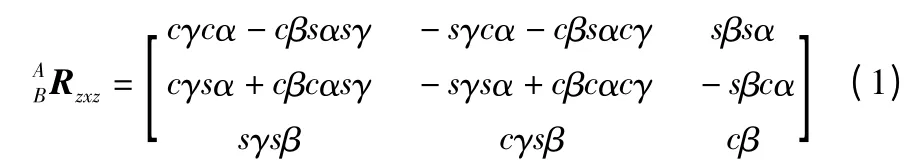
式中s 和c 分别表示正弦和余弦函数，α、β 和γ 为欧拉角。

根据图1，铰接点Bi在动坐标系o-xyz 下的坐标可以表示为BBi=(xBi，yBi，zBi)T，将其在参考坐标系下表示:

杆i 的杆长向量可通过下式得出:

其中Ai为定平台上铰接点Ai在参考坐标系下的位置向量，那么杆长Li为:

则各杆沿着杆长轴线方向的单位方向矢量为:

Bi点的速度可以通过对式(2)求导得到:

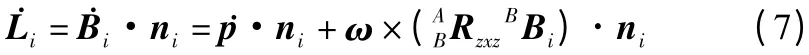
上式还可以表示成如下形式:

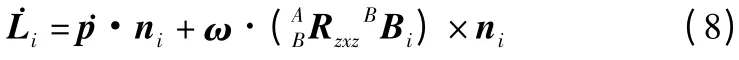
将其化为矩阵形式可得:

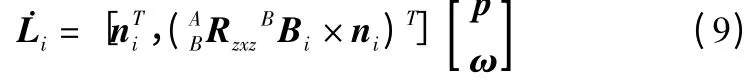
对于全部六根杆，可以写成下列形式:

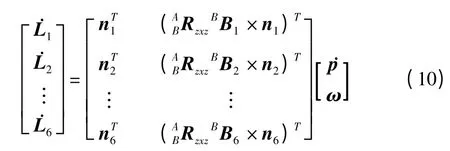
简记:

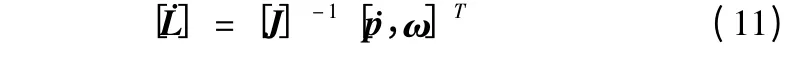
其中:

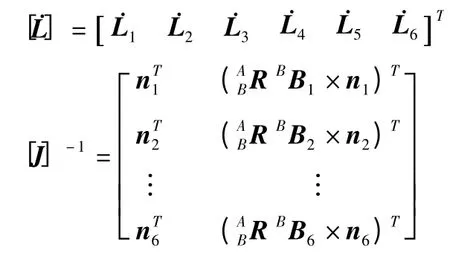
［J］－1是机构的逆速度雅可比矩阵，反应了末端速度到关节速度的映射关系。

2 并联机构的振动模型

并联机构的运动平台及固定平台的刚度远远大于支链的刚度，故可将其看作为刚体［9］。为了得到机构的振动动力学方程，假定驱动杆、球铰和万向节为弹性元件，并且假设运动副之间足够光滑，可忽略这些运动副之间的摩擦力。并联机构的振动特性很大程度上受到动平台位姿的影响，而此型并联机构有6 个自由度，位姿千变万化，这就增加了研究的难度。

基于以上假设，提出了Stewart 型并联机构的振动模型，如图2 所示。由于机构的6 个驱动杆是完全相同的，所以仅画出了一条支链的振动模型。

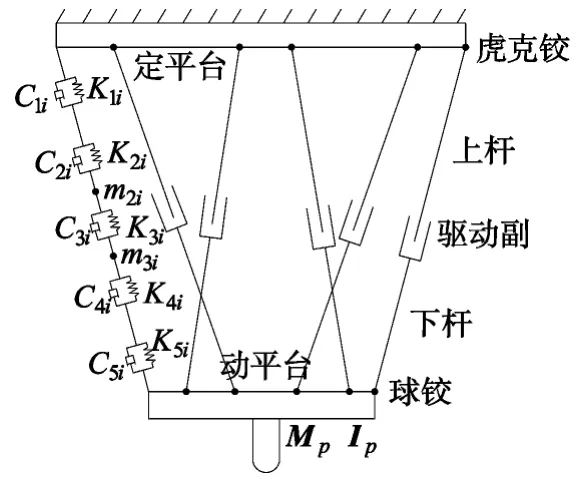
图2 并联机构振动模型简图

图中Mp和Ip分别为动平台的质量和转动惯量矩阵;m2i和m3i(i=1，…，6)分别表示驱动杆上杆和下杆的质量;K1i，K2i，K3i，K4i和K5i分别表示万向节、驱动杆上杆、滑动副、驱动杆下杆和球铰的刚度系数;C1i，C2i，C3i，C4i和C5i分别代表万向节、驱动杆上杆、滑动副、驱动杆下杆和球铰的阻尼系数。假设s1i、s2i、s3i、s4i和s5i表示万向节、驱动杆上杆、滑动副、驱动杆下杆和球铰的形变。

建立并联机构的振动方程之前，首先应分析各个杆件与动平台之间的受力关系，图3 为机构的受力分析图。

在图中，BFex和BTex分别表示作用于动平台铣刀上的外部力和外部力矩。

动平台的牛顿方程和欧拉方程分别为:

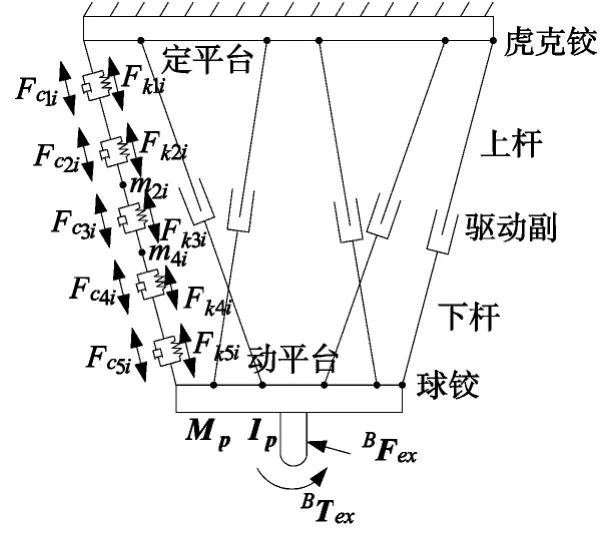
图3 并联机构的受力分析图

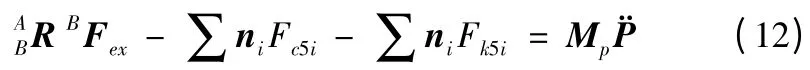
式中，φ = (α，β，γ)，rBi表示动平台球铰的位置矢量，Bro表示铣刀受力点的位置矢量。

由于支链的各个元素之间是串联关系，可得:

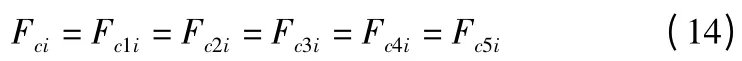
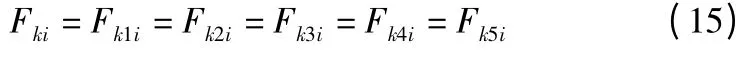
又因为:

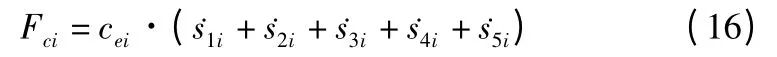
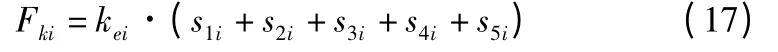
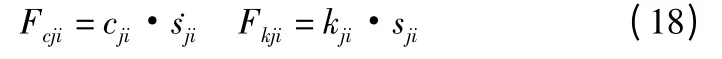
式中cei和kei为杆i 的等效阻尼系数和刚度系数。

由以上各式可得:

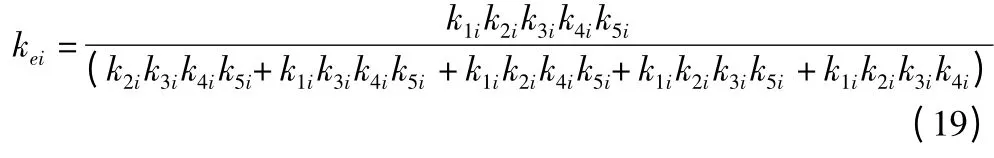
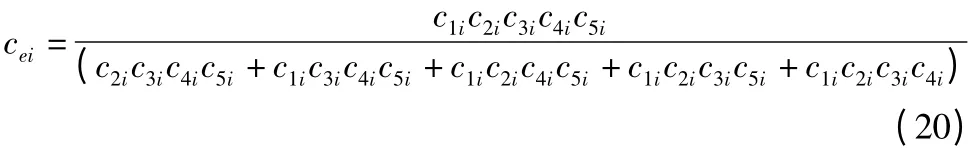
定义q = [ p φ]T，联立式10、12－2 即可得到Stewart 型并联机构的振动动力学方程:

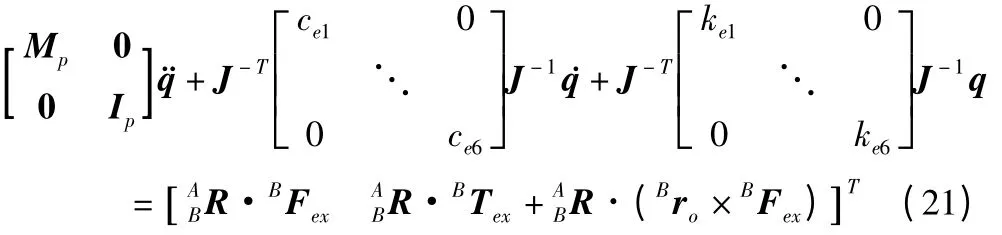
3 并联机构的振动特征研究

下面来研究Stewart 型并联机构的振动特性，假设该机构驱动副采用滚珠丝杠副。首先，定义该机构的尺寸参数和刚度系数。对于驱动杆上杆和下杆的刚度，可以通过经验公式计算求得，至于万向节与进给滚珠丝杠副的刚度系数可以参考文献［10］和文献［11］。表1 列出了该机构的相关参数。

表1 并联机构的有?关参数

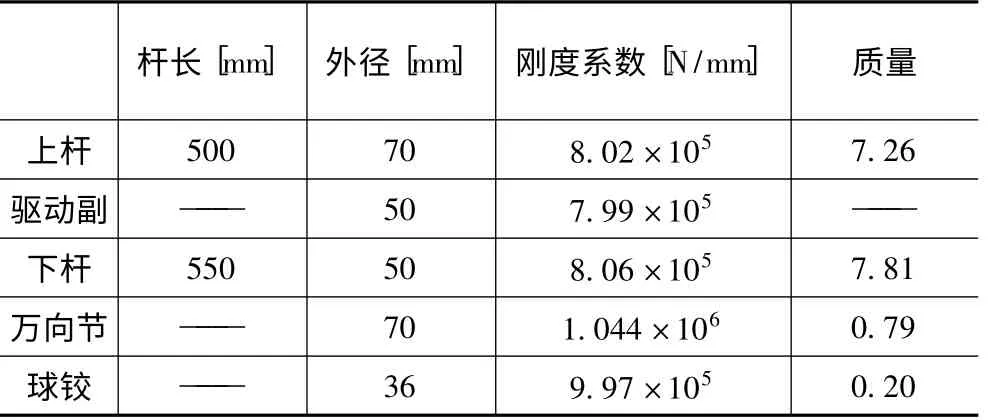
(续表)

表2 是并联机构动平台14 种位姿下的位置坐标和姿态角。

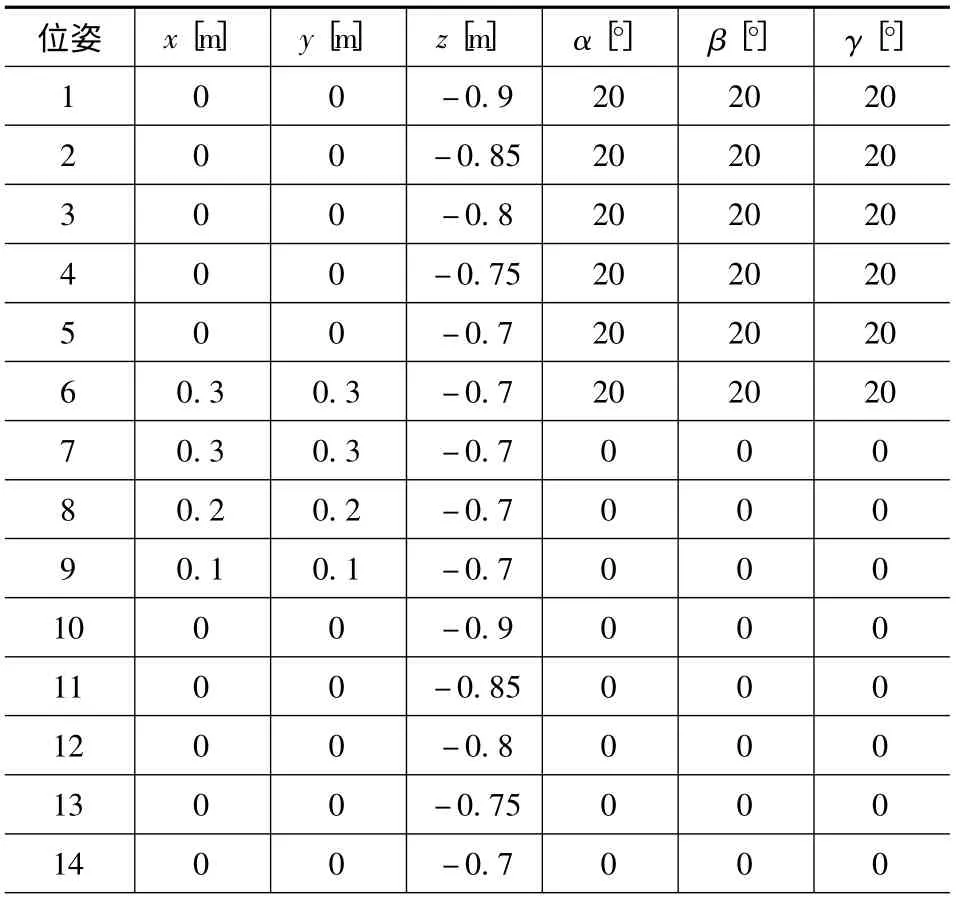
表2 动平台的位置与姿态角

根据给出的机床参数，结合该机构的振动动力学方程，即可求得各个姿态下的固有频率。表3 为所列的14 种动平台位姿下的固有频率。

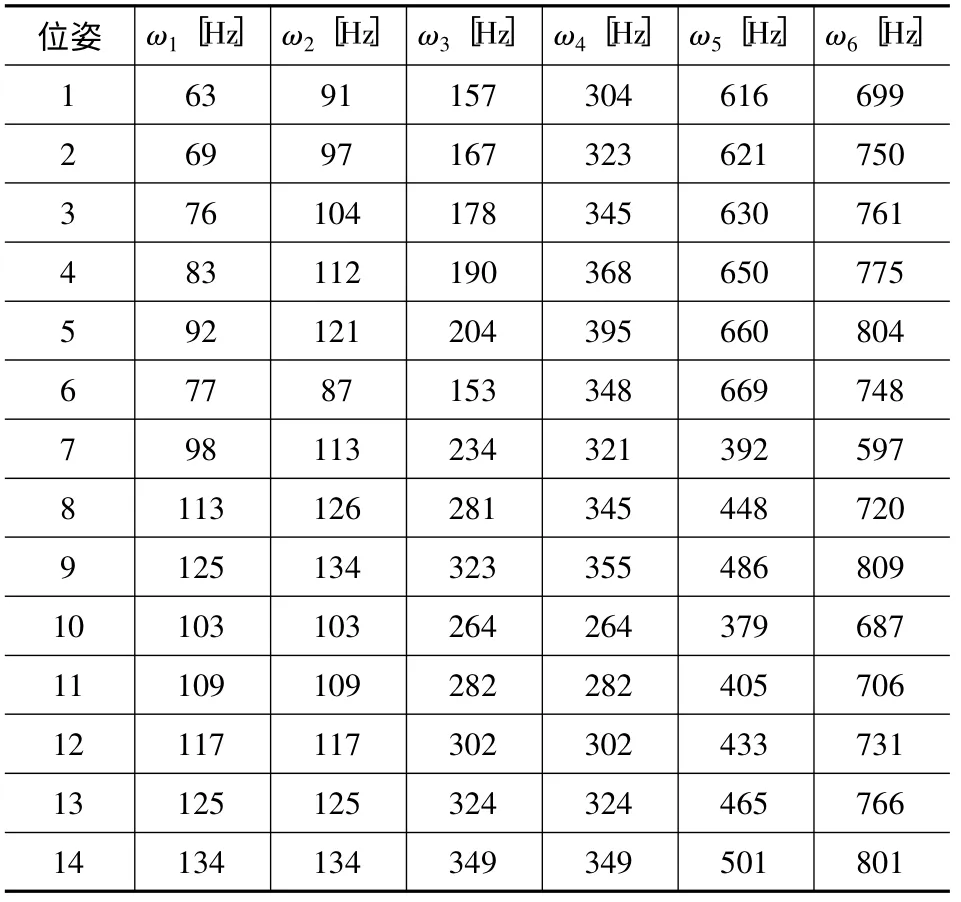
表3 动平台各姿态下的固有频率

为了验证所建立模型的正确性与否，下面利用ANSYS 软件进行有限元分析验证说明。按照上述参数建立了该型并联机构的三维模型，然后导入ANSYS中进行网格划分和计算分析。图4 为划分网格后的有限元模型。

在划分完网格建立有限元模型后，即可进行模态分析，根据表2 所列的各个动平台位姿进行分析。图5 为有限元计算的一个示例。

图4 并联机构的有限元模型

图5 ANSYS 计算示例

表4 即为利用ANSYS 软件计算所得的14 种位姿下的固有频率值。

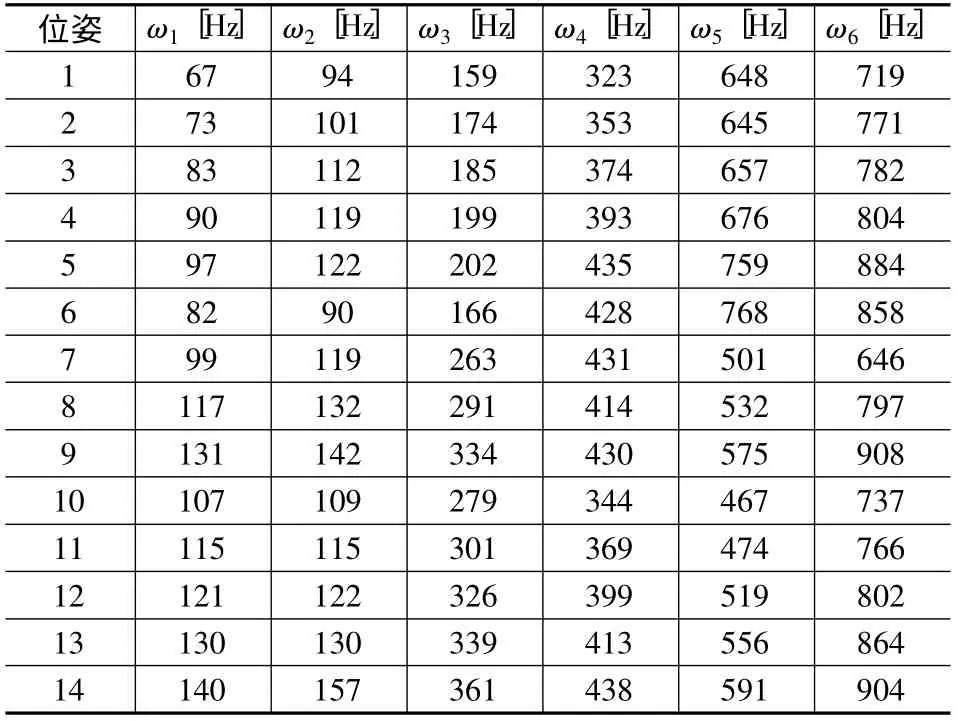
表4 ANSYS 运算得到的固有频率

对比ANSYS 计算的仿真值与理论推导值，可以发现两者相差不大，充分验证了所建立的振动动力学模型的正确性。根据所列的各个位姿下的固有频率，得到了该机构的固有频率分布图。通过分布图可以清晰地看出不同位置姿态下的固有频率变化情况，如图6所示。

通过表2、3 和表4 的数据分析及图6 的变化趋势可知，工作平台的固有振动频率和动平台的位姿有着很大的关系。位姿不同，则该机构的固有振动频率将发生很大的变化。这与传统的加工机床有着很大的区别，传统加工机床的各阶固有频率基本上稳定的，不会有明显的变化。

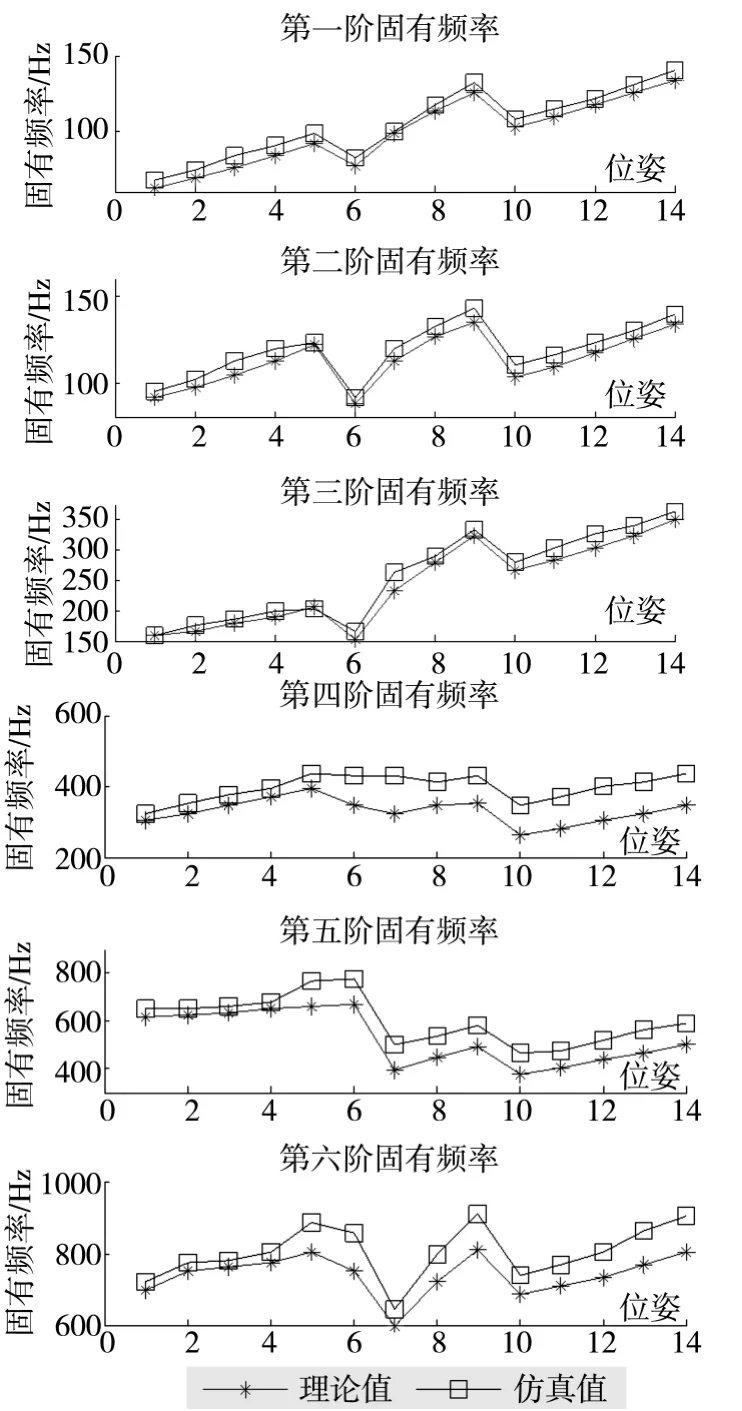
图6 机构的各阶固有频率分布图

同样姿态的条件下，当动平台远离定平台的，机构的固有频率有下降的趋势，即动平台的位置越低，固有频率越低。因此高的切削速度可以防止切削加工的切削不稳定性，这一特性也正说明了为何并联机床更适合进行高速切削加工这一特点。但是其位置较低时，机床的刚度相对于高位置时较小，故适合进行小切削量的高速精加工。当动平台的中心位置相同时，动平台姿态与定平台姿态不重合时的前几阶固有频率要比重合时高。当动平台高度和姿态恒定时，并联机床的前几阶固有频率随着动平台在水平面上移动而降低，并且移动的位移越大，降低得越多。这些特性对于并联机床铣削加工具有重要的指导意义。

4 结论

通过对Stewart 型并联机构进行运动分析，得到了该机构的Jacobian 矩阵。将机床的驱动杆、球铰和万向节视为弹性元件，并且忽略这些运动副之间的摩擦力，运用牛顿欧拉法对其进行力学分析，得到了Stewart型并联机构的振动动力学方程。最后研究了该机构的振动特性。

在动平台中心位置不变的情况下，动平台姿态与定平台姿态不重合时的前几阶固有频率要比重合时高。当动平台高度和姿态恒定时，并联机构的前几阶固有频率随着动平台在水平面上移动而降低，并且移动的位移越大，降低的幅度越大。同样姿态的条件下，动平台的位置越低，固有频率也相应越低，因此并联机床更适合进行高速切削加工。

通过分析可知，与传统机床不同，并联运动机床在切削加工过程中，随着工作平台的位姿变化，其固有振动频率有很大的不同。所以在进行 并联床结构设计时要充分考虑到所要求的刚度和固有频率指标，适当调整机构参数。

［1］ C. Gosselin，Stiffness mapping of parallel manipulators ，IEEE Transactions on Robotics and Automation，1990，6(3):377－382.

［2］K.Miller and R.Clavel. The Lagrangze-based model of DELAT-4 robot dynamics，Robotersysteme，1992，8(1):49－54.

［3］J. Wang and C. M. Gosselin，A new approach for the dynamic analysis of parallel manipulators，Multibody System Dynamics，1998，2(3):317－334.

［4］B. Dasgupta，T.S. Mruthyunjaya，A Newton—Euler formulation for the inverse dynamics of the Stewart platform manipulator，Mechanism and Machine Theory，1998，33(8):1135－1152.

［5］S. F. Chen，I. Kao，The Conservative Congruence Transformation for Joint and Cartesian Stiffness Matrices of Robotic Hands and Fingers，The International Journal of Robotics

Research，2000，19(9):835－847.

［6］J. M. Selig，X. Ding，Theory of vibration in Stewart platform，Proceedings of the IEEE International Conference on Intelligent Robots and Systems，Maui，Hawali，USA，2001:2190－2195.

［7］Kim HS，Design and control of Stewart platform-based machine tool. PhD Dissertation，Graduate School Yonsei Univ.，South Korea，1999.

［8］Y.Cheng，G.Ren，and S.Dai，The multi-body system modeling of the Gough-Stewart platform for vibration control，Journal of Sound and Vibration，2004，27(1):599－614.［9］C. Gosselin，Stiffness mapping for a parallel manipulators，IEEE Transactions on Robotics and Automation，1990，6(3):377－382.

［10］王德会，方菲. 整体弹性关节刚度系数的计算［J］. 机械工程与自动化，2012，171(2):168－169.［11］杨祖孝. 进给滚珠丝杠副传动刚度的计算［J］. 制造技术与机床，1999(7):12－14.