大型复杂曲面工件的重心倾测方法研究*

梁延德，郭 超，王治雄，何福本，孙捷夫

(大连理工大学 机械工程学院，辽宁 大连 116024)

0 引言

具有复杂曲面的大型工件，在加工过程中，由于制造不精确、材料不均匀以及安装不准确等非设计因素的影响，导致实际测量重心位置和理论设计重心位置不重合，无法满足设计要求，造成动平衡性能指标下降。由于此类问题是在制造加工中产生的，无法通过理论设计进行误差确定和消除，因此需要对工件的加工质量进行评价，通过实验的方法对重心准确测量，进行相关补偿，改善工件的平衡性能。

传统的重心测量方法主要有:悬挂测重法、复摆测重法、配重平衡法和平面测定法等［1］。其中，悬挂测量方法主要用来对厚度均匀的物体进行平面重心测量;复摆测量方法在物理上主要用来测量刚体的转动惯量和重力加速度，适用于小体积刚体重心的粗略测量［2］;配重平衡测量方法是在进行工件重心测定时，通过调整传感器的安装位置和配重质量，使工件达到平衡状态，并根据力矩平衡关系，计算得到粗略的工件重心位置，但是对工件的形状尺寸有一定要求［3］;而目前的平面人工测定法仅能够粗略地计算工件重心的平面位置［4］，方法效率较低，精度较差。以上重心测量方法，虽然具有原理简单、操作简便的特点，但在对大型复杂曲面工件的进行重心测量时，上述方法在管理操作、执行效率、误差控制以及测量范围等方面都有局限性。

船用螺旋桨桨叶是典型的大型复杂曲面工件，若各桨叶的重心对桨轴产生的力矩不同，螺旋桨在工作时会产生动不平衡，影响其推进性能和使用寿命。因此，本文以大型船用螺旋桨桨叶为研究对象，对其重心测量方法理论和实际测量手段进行研究，设计出一种新颖的重心精确测量和定位装置，为船桨的平衡补偿和再制造加工提供可靠依据。

1 测量原理

1.1 重心倾测法

本文针对螺旋桨桨叶体积大，形状复杂的特点和螺旋桨设计性能要求，结合传感器技术，提出一种新颖的桨叶重心测量方法:分别对处于水平位置和某角度倾斜位置的桨叶进行静态测量［5-7］，通过称重传感器读取相应支撑力数值，根据力矩平衡理论和坐标系转换方法，计算得到桨叶的实际重心位置。这种以倾转工件进行重心精确测量的方法，简称为重心倾测法。基于此方法，本文所设计的用于螺旋桨桨叶的重心倾测系统结构如图1 所示。

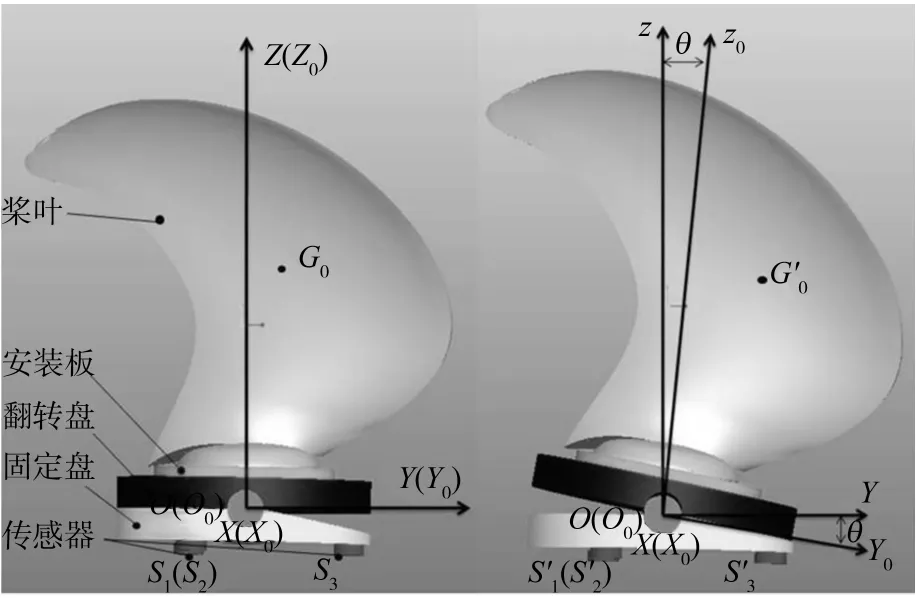
图1 测量系统结构示意图

由图1 可知，倾测系统主要由安装板、翻转盘、固定盘和传感器等部件组成。系统分别设计了两个笛卡尔直角坐标系:固定坐标系O-XYZ 位于固定盘上，相对地面保持不动;工件坐标系O0-X0Y0Z0位于翻转盘上，随翻转盘转动。工件坐标系是由固定坐标系绕X 轴旋转一固定角度θ 得到的，两坐标系原点O 与O0为空间内同一点。固定坐标系X 轴与工件坐标系的X0轴为空间内同一直线，即工件倾转轴线。传感器部分由三个相同型号的称重传感器s1、s2、s3构成，且三者在同一水平面内，构成正三角形，其在固定坐标系O-XY 面内的投影如图2 所示。由图2 可知，正三角形外接圆圆心即为固定坐标系原点O，外接圆半径为R。传感器位置固定，不随工件的倾转改变。

1.2 重心位置计算

根据上文提出的测量原理，倾测系统在工作时有两种工作姿态，即图1 中所示左图为水平姿态和右图为倾斜姿态。图2 所示，左图为桨叶在水平姿态下重心G0在测量坐标系水平面内的投影;右图为倾斜姿态下桨叶重心G'0在测量坐标系水平面内的投影。在两种测量姿态下，桨叶重心相对工件坐标系位置不变，坐标均为(x0，y0，z0)。

图2 重心在固定坐标系内投影示意图

根据两坐标系间的关系可以知道，在水平姿态时，桨叶重心G0在两个坐标系下的坐标关系为:

在倾斜姿态时，倾斜角为θ，桨叶重心G'0在两个坐标系下的坐标关系为:

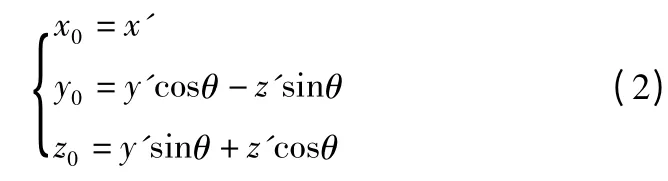
根据力矩平衡原理［5］，在测量坐标系内在水平姿态下建立关于X 轴和Y 轴的力矩平衡关系式。

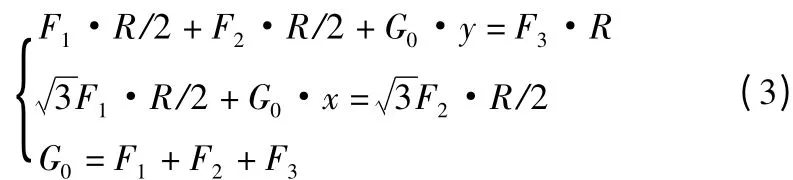
其中，F1、F2、F3为传感器支撑力数值，R 为正三角形外接圆半径，由式(3)可得到:

同理，在倾斜姿态下建立关于X 轴和Y 轴的平衡关系式，可以得到:

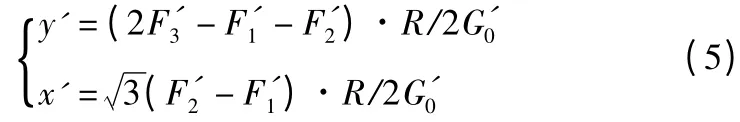
坐标(x，y)由式(4)可知，结合式(1)，则可知在水平姿态时，桨叶坐标系下坐标(x0，y0)。

由式(2)可知，y0=y'cosθ－z'sinθ 且y0=y，则可以得到:

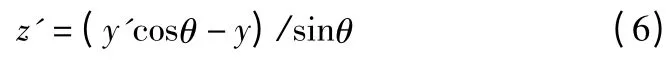
将式(6)带入(2)，可得:

综合式(1)和(7)可以得到重心在桨叶坐标系下的坐标表达式。

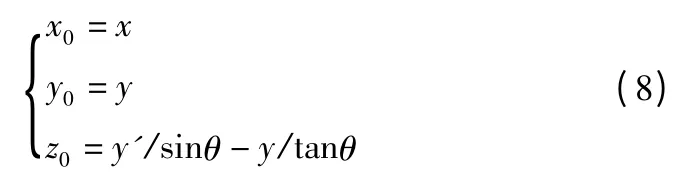
重心倾测法原理简单，以此为基础的重心倾测系统，具有结构简洁、操作方便、实用性强的优点，应用传感器技术，测量精度较高。测量时，采用立式装夹方式，对工件尺寸限制较小。

2 实验与结果分析

2.1 实验设备简介

根据本文提出的重心倾测系统，设计研制了相应的重心倾测设备。设备的安装板根据桨叶底部与桨毂之间的安装定位孔设计了相应的连接结构。在进行重心测量时，桨叶通过安装板装夹固定。安装板和翻转盘之间采用圆周均布的螺栓固定方式。翻转盘与固定盘直径为1400mm，采用铸铁材料，强度高，不易发生变形，通过铰链连接，翻转盘可绕倾转轴转动。重心测量设备的测量范围为100kg 至600kg，以电机带动推杆实现工件倾转，翻转盘倾转角度为8°，由步进电机和行程限位开关共同控制决定。传感器采用轮辐式称重传感器［8-9］，量程1000kg，误差范围±0.03kg。测量机外部设计有防尘罩，减少因工作环境中的浮尘进入等因素对测量精度产生影响。基于Visual Basic 6.0 开发的倾测系统软件，可以提供完善的操作命令输入和实时数据监测，实现系统的姿态控制和测量过程中的数据存储等功能。

2.2 实验与数据处理

实验开始前，应打开重心测量机电源开关，进行测量机的预热，使整个测量系统达到热平衡状态［10］，减小因系统内热迁移造成的测量精度下降。

每次实验时，需在桨叶装夹前，进行水平和倾斜两种姿态下的测量机自重清零测量，以消除设备本身对测量结果的影响。清零完成后，将桨叶安装在测量机上开始进行测量。首先进行水平姿态下的测量，待系统稳定后，采集数据，读取传感器数据F1、F2、F3并存储。之后进行倾斜姿态下的测量工作，记录传感器数据F'1、F'2、F'3。

每组实验进行三次计数测量，数据记录完毕后，将桨叶卸载，再次装夹后，进入下一组计数测量。这样的实验安排是为了消除在桨叶装夹过程中人为因素产生的偶然误差，提高测量的精确性。

实验用桨叶重量321.5kg，重心坐标(－47.0，51.0，685.5)，单位mm，重心位置测量最大允许误差为±0.5mm。

在测量系统准备工作完成后，进行了多次实验。部分实验数据如表1 所示。

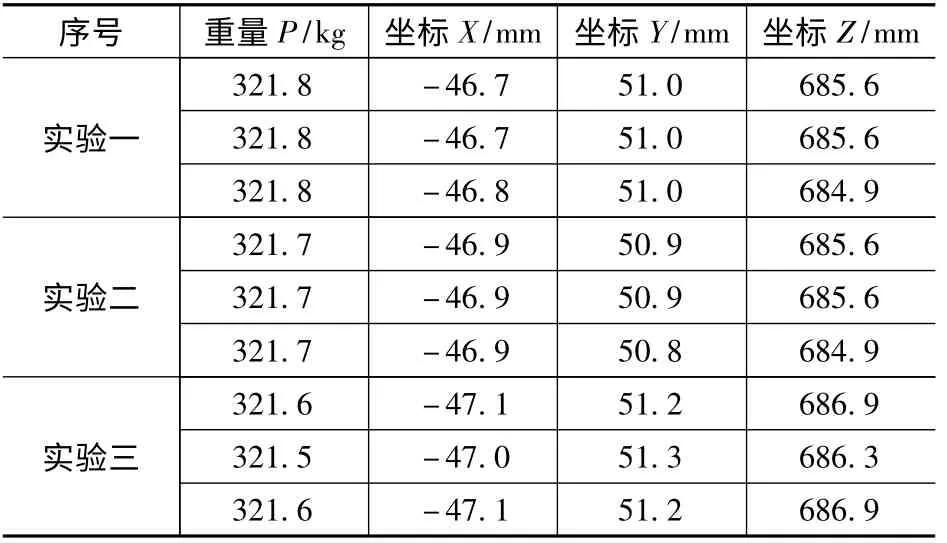
表1 实验测量结果

本文采用拉依达准则对测量得到的实验数据进行粗大误差分析［11］。分析结果表明，实验三中第一和第三组测量数据属于粗大误差，应舍弃。对表1 中数据进行分析可得表2。

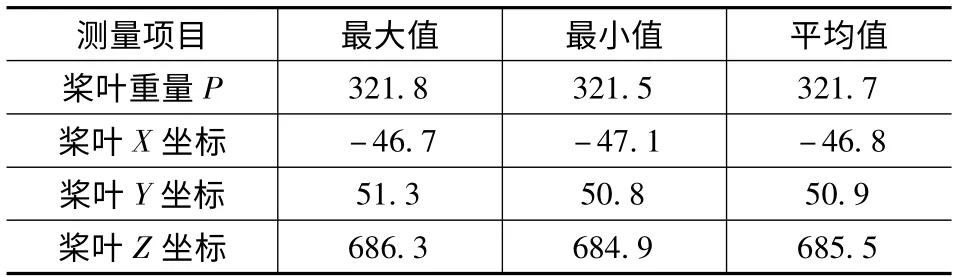
表2 测量均值与变化范围

由表2 可知，桨叶重量测量平均值为321.7kg，误差范围为±0.3kg;测量得到的桨叶重心坐标平均值(－46.8，50.9，685.5)，单位mm，测量误差在允许测量误差范围内。

依据表1 和表2，将剔除粗大误差后的实验数据绘制成如图3 所示的测量误差曲线图。由图3 可以看出，测量系统具有较高的测量精度，且在多次装夹过程中，系统都表现出了较好的重复性。测量误差曲线图出现较小范围内的波动，其原因主要是由于在测量中不可避免的引入的人为误差造成的，规范实验操作可以减小其影响。

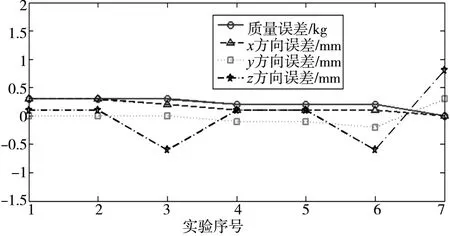
图3 测量误差分析曲线图

3 结论

与传统的重心测量方法相比，本文所提出的大型复杂曲面工件的重心倾测方法，具有原理简单、实用性强、适用范围广和测量精度高的特点。该方法能大幅提升测量效率，不仅适用于大型复杂曲面回转类工件的重心测量工作，还可对非回转类工件的重心位置和重量进行精确测定，其测量结果对于工件的平衡性能指标具有参考价值，为工件的加工提供可靠的依据，满足设计要求并提高使用寿命。

［1］韩向东. 机械工程力学［M］. 北京:机械工业出版社，2002.

［2］袁昌盛，宋笔锋. 改进复摆法测量转动惯量的方法和设备研究［J］.中国机械工程，2006，17(6):598－600.

［3］王存堂，胡红波，刘志勇. 船用螺旋桨静平衡计算机检测原理与实验研究［J］. 船舶工程，2011(2):41－43.

［4］李芳. 桨叶重心检测系统设计［C］. 中国智能交通年会优秀论文集，北京，2012.

［5］Gao Z H，Mao J D. Dynamic Weighing Technology Combining Parameter Identification［C］. 第三届国际仪器科学技术学术研讨会论文集，西安:2004.

［6］潘若刚，曹雷，王巍. 高精度全机重心测量方法的探讨［J］.飞机设计，2010，30(2):1－4.

［7］唐勇超，梁延德. 翻转法测量工件重心技术研究［J］. 机械研究与应用，2012(2):44－46.

［8］杨满兴，梁栋栋，魏立峰，等. 在线智能重量测量测量仪的设计［J］. 仪表技术与传感器，2007，23(4):187－189.

［9］黄长艺，卢文祥，熊诗波，等. 机械工程测量与测试技术［M］. 北京:机械工业出版社，2000.

［10］Fu L，Hong Y. Thermal Equilibrium Reached by Interaction between Two Identical Systems［J］. Communications in Theoretical Physics，2008，49(6):1461－1462.

［11］郑叔芳，吴晓琳. 机械工程测量学［M］. 北京:科学出版社，1999.