基于热量分布的布朗尼饼烤盘最佳形状探索

王 睿

大连交通大学， 辽宁大连 116000

0 引言

制作布朗尼饼的两个重要工具是：烤箱和烤盘。而影响布朗尼饼口感的因素有很多，比如：烤箱内的热量分布是否均匀，烤盘的形状等等。我们了解到烤箱的作用机理：大部分的电烤箱有内置风扇，因此在预热之后烤箱内的热量是均匀分布的。针对目前市场销售较为广泛的三种常见的烤盘：方形烤盘，圆形烤盘，边缘型烤盘。考虑到人们对于烘焙的布朗尼饼口感评价的直接因素便是在烘焙过程中在预热过后的布朗尼受热是否均匀。因此探讨圆形烤盘热量分布便成为了问题的核心。在布朗尼饼的烘烤过程中，通常需要对烤炉进行预热，当炉内温度达到额定值时，将平底锅放入炉中进行烘烤，因此在整个烘烤过程中可以假定炉内温度是保持不变的。可只考虑热传导现象，因为即使热量通过炉内空气自然对流进行传播，其相比于热传导也是可以忽略的。由于平底锅的厚度可忽略并且在初始状态下炉内的温度已经达到了额定值，无论平底锅的形状如何，热量都是由平底锅的外边缘向内部传递，所以一般学者将问题简化为了稳定状态的二维热传导问题。该过程通常可以利用下面的二维热传导方程[4]来描述：

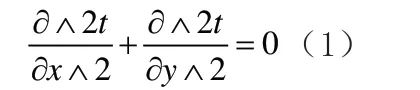
由于上述方程求解较为复杂且无法求出解析解，所以现阶段国内外的很多学者对布朗尼盘的最佳形状进行了探索，并提出运用有限元，偏微分方程等方法进行数值求解，并通过ANSYS 和COMSOL 进行仿真，但是到目前为止，由于烤盘的边界温度条件尚未研究出统一结果，而且在仿真过程中ANSYS 和COMSOL 等软件在使用neumann 边界条件还是dirichlet 边界条件或者混合边界条件仍然存在一定的争议，因此我们希望能够寻找到一个更加简单的模型求解出烤盘的热量分布。

1 热量分布建模的建立

1.1 基本模型

为了能够得到更加清晰的能量分布描述，可对布朗尼饼烘烤的过程进行模拟，以便对平底锅的外部形状和烘烤状态进行实时控制，我们考虑对热传导过程进行分析，即通过参考普朗克提出的能量量子化思想：将能量看作能量子，能量子会从能量多的地方流向能量少的地方。同时因为有预热处理，可将在内部空间中温度的均匀分布（温度是热能分布的直观体现），等效为能量子的均匀分布。

当放入平底锅时，假设此时烤箱内平底锅所占用空间的能量子总和为零。根据量子化思想，由于这部分空间的能量子密度低于非平底锅占用空间的能量子密度，能量子将会从其他空间流入平底锅所在空间，这个过程便可等效为以平底锅边界作为热源，向其中心进行热传导，即能量子向中心汇聚。由于平底锅的边缘形状需要多个参数才能进行细致地刻画，处理起来较复杂。这里采用另外一种简化的处理方法，即将平底锅和锅内的布朗尼饼看成一个封闭的系统，该系统是能量保守系统，考虑到平底锅形状的对称性，则将从平底锅外边缘向内发射能量子的过程看作是从平底锅内部的中心点向外发射能量子的逆过程。通过查阅文献[10][11]可知，能量子沿着边缘到中心的矢径服从正态分布，其一维点热源热量分布为：

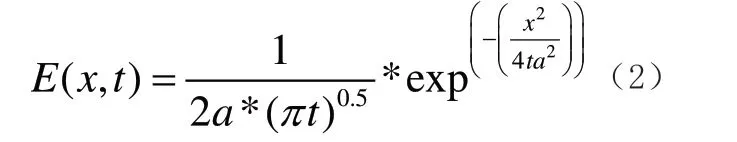
其中：

E（x，t）为在时刻t，x 点处的热能；

a 为初始时刻点热源与热势能零点的初始温度差；

t 为时间，当t 趋于无穷时，E（x，t）趋近于一条与x轴重合的直线。

鉴于此，我们将其扩展到二维区域，可得到二维点热源热量分布为：

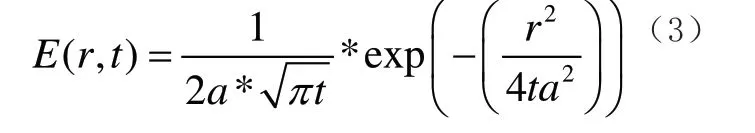
其中：r^2=x^2+y^2。

为了更直观地体现热量分布，我们根据上述二维点热源热量分布函数绘制了热量分布图：

图1 二维点热源热量分布图

通过上述公式利用Matlab 模拟出圆形烤盘的能量分布如图所示，由图，我们将能量划分为7 个能区，由高到低分别用颜色红，橙，黄，绿，靛，蓝，紫表示。

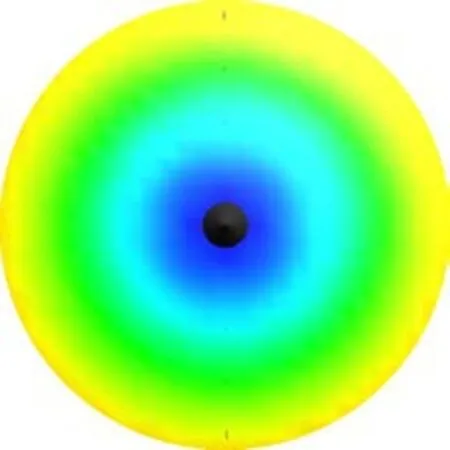
图2 t=10 时能量分布图

图3 t=25 是能量分布图

从能量分布图上可以看出，圆形烤盘的边界始终为同一能区。圆形烤盘的能区数逐渐减少，说明随着烘烤时间的增长烤盘内部的热量会逐渐趋近均匀分布。没有红，橙色能区说明不会出现受热过度而烤糊的情况。

1.2 模型改进

上述能量分布图是在边界无穷大的理想情况下根据热量分布函数公式绘制出的，而实际问题中，由于受到烤盘边界的影响，发射出去的能量子不会始终以一种方式传播，因此需要修正之前的模型。这里我们将外边界视为无穷远点，因此图形的尺度发生了变化。从而对公式（3）中r 进行修正，将由二范数定义的距离修改为由椭球范数定义的距离，二者在拓扑意义下是等价的。

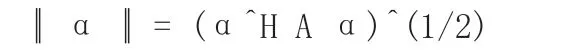
上式中矩阵A 与外边界直接相关，比如对于圆形区域，A可取为：

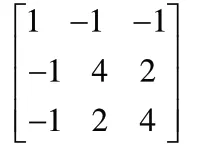
根据修正后的模型利用Matlab 绘制出新的能区分布图：

图4 修正后的能区分布图

将图4 与图2、图3 比较，不难发现：两个模型所分析出的圆形烤盘能量分布大致相同，验证了模型的准确性和稳定性。

2 模型的校检

通过查阅的资料，我们将模型与COMSOL[7]和ANSYS[8]软件仿真得出的图形与图4 进行了比较，如下图。

由图，我们发现我们的模型与用COMSOL 软件和ANSYS 仿真得出的图形没有差异，而且我们的模型避免了对有限元等专业知识的运用，并且避开了现在cosmol 软件及ansys 软件分析中遇到的边界选择问题和导热过程中导热函数选择的难题。因此更具备通用性，对于那些尝试进行布朗尼烘烤的人员而言也更加简单通用。

图5 COMSOL 软件的仿真能量分布图

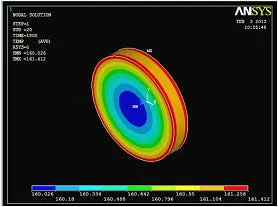
图6 ANSYS 软件的仿真能量分布图

3 结论

通过对我们的模型进行分析，我们发现使用布朗尼饼烤盘有均匀的热量分布，并且与其他软件仿真得出的结论一致，说明模型构建合理可信；同时模型避开了复杂的热量边界条件及目前科学界仍有争议的导热函数的选择，仍得出了圆形烤盘具有较好的热量分布结论，并通过仿真使得人们能够更加直观的得出圆形烤盘具有较好的热量分布，而这也符合了实际的布朗尼烤盘的形状。

[1]郑志敏，李红平.电烤箱设计规范.广东新宝电器股份有限公司研发中心， 2009，5.

[2]姬瑞海.产品造型材料与工艺.北京交通大学出版社， 2010，1.

[3]钟志惠.西点生产技术大全.化学工业出版社，2012.8.

[4]杨世铭，陶文铨.传热学，4版，高等教育出版社，2006，8.

[5]Dhandapani， S.，Navaneethakrishnan，K. and Srinivasan，P. P.2006， Heat transfer and heati ng rate of food stuffs in commercial. Sadhana. India，Department of Mechanical Engineering， Kongu Engineeri ng College ： Vol. 32，Part 5， October 2007，pp. 535-544.

[6]Tony F. Chan and Luminita A. Vese. Active Cont ours Without Edges.IEEE Transactions Image Processing.Vol.10，No.2，February 2001.

[7]http：//wenku.baidu.com/view/7b159cc3524de518964b7df4.html.8.31，2013.终极布朗尼烤烤盘.

[8]Song E，Li Shiguo： Technique and application of thermal field analysis for electro-thermal products based on ANSYS. Machinery Design and Manufacture.(2005). Number10，117-119.

[9]曾谨言. 量子力学，4版，科学出版社，2007，1.

[10]李福善，空翠翠.曲阜师范大学学报.2006，7，32(3).

[11]谷超豪，李大潜.数学物理方程[M].2版，北京.高等教育出版社，2002.