高校学生考试成绩分布的正态性检验
2013-12-22李萍
李 萍
(陕西学前师范学院计算机系,陕西西安 710100)
考试是教学工作的重要环节,是检验学生学习效果和教学效果的主要手段。用科学的方法对学生的考试成绩进行鉴定与考核,可以对教学质量进行定量的评价与分析。本文从提高教学质量出发,对学生考试成绩分布作正态性检验(质量指标之一),从而较准确地评判考试的状况,以期对改进我们的教学工作提供参考。
1 成绩正态分布检验的意义
按照教育测量学的原理和考试系统的特征,对考试成绩进行正态分布检验的意义主要有两点[1]。一是许多重要的考试质量评价指标[2]的计算都以成绩服从正态分布为前提,例如在对考试成绩及试题参数的统计过程中,使用的均值、方差等主要统计参数的估计和检验,只适用于正态分布或近似正态分布的情况,因此在使用这些统计方法前,必须进行正态性检验。二是用于对考试成绩的解释,不同的成绩分布可以解释为试题的难度分布情况和学生的学习情况,或者在不同类型的考试中可以解释为教师的教学情况。
研究证实自然人群中个体智力分布特征为处于中等智力附近的个体数量较多,由中间向两端(智力低下和智力超强)数量逐渐减少,从形态上看是一条单峰、对称呈钟形的分布曲线,该曲线符合统计学上的正态分布(normaldistribution)[3]。在教学过程中,教师如果按照课程的教学大纲和教学基本要求组织教材,结合学生的实际选定适当的教学方法,备好课,讲好课,认真地批改作业,那么学生成绩应受智力影响较大,则服从正态分布。同时成绩的正态分布性也反映了试题的知识点全面,难易程度适中,学生对本门课程在知识结构和能力发展方面已达到基本教学目标。因此,成绩分布的正态性检验可为教师提高教学质量和教学行政部门改进教学管理提供科学依据。
学生总体学习成绩分布有以下几种情况:(1)正态分布:说明测试结果与学生的实际情况一致,试题的知识点全面,难易程度适中。(2)正偏态分布:说明试题难度偏高。(3)负偏态分布:说明试题难度偏低。(4)双峰型分布:说明试题存在两极分化现象,即难度偏高的和难度偏低的项目较多,而中等难度的项目偏少,项目难度的分布缺乏梯度,不够合理。(5)平坡型分布:说明试题中各种难度的项目比例接近,梯度较大(如图1)。
2 χ2检验
成绩是否服从正态分布通常采用直方图描绘分数分布曲线的方法大致地判断,但没有定量的标准。下面介绍一种简单实用的正态性检验方法,拟合优度的χ2检验法[4],从而可以对试题质量进行粗略的评价,实现对教学质量的定量分析。

图1
χ2检验是利用随机样本对总体分布与某种特定分布的拟合程度的检验,也就是检验观测值与理论值(期望值)之间的紧密程度。当我们研究n(n>2)个事件时,可以测定n个观测值与相应的理论值之间的差异,为此而构造的统计量称为χ2统计量。χ2是1900年由英国统计学家K.Pearson提出的定理。该定理说明,当样本容量充分大时,样本分成k类,每类实际出现的观测频数用f0表示,其理论频数用fe表示,则统计量Σ(f0-fe)2/fe服从自由度为k-1的χ2分布。在非参数统计中,拟合优度的χ2检验法是检验总体是否来自已知分布函数的常用方法,它的优点在于不管总体分布函数是何类型,都可用此方法。
但是考试成绩总体是一个很特殊的总体,用χ2的拟合优度检验法对其进行正态检验时存在明显缺陷。例如,一批含有负值但有对称性的数据,经χ2检验后也可被认为服从正态分布,但它作为学生的考试成绩就不具有实际意义。所以,对考试成绩总体进行正态分布检验时,仅按通常χ2拟合优度检验是不够的。设学生成绩总分为W,根据教育统计学的基本原理,在正常的教学条件下,学生成绩应该服从均值为W*70%,标准差为W*10%的正态分布。因为均值和标准差的值过低或过高,说明我们在教学过程中贯彻教学基本要求,组织课堂教学,课程考试等工作环节出现了较大的失误,此时进行正态性检验已失去应有的实际意义。为了能反映在正常教学条件下,教和学的具体情况,找出教学过程中成功的经验和存在的问题,在对考试成绩这一特殊总体进行χ2的拟合优度检验时,合理服从正态分布的成绩应满足以下条件:
Ⅱ 根据概率论中的3σ原则,标准差σ∈〔5,15〕
Ⅲ 按通常拟合优度的χ2检验法,检验学生成绩总体服从正态分布。
3 成绩正态分布的χ2检验
设x1,x2,…,xn是从学生成绩总体中提取的样本试卷,并把成绩区间划分为k个区间,即(0,t1),(t1,t2],… ,(tk,W),从而全部n个样本分成k组。用Vi表示x1,x2,…,xn落入第i段的个数(观测频数),(i=1,2,…,k),Vi/n表示频率。
判断是否满足条件ⅠⅡ,若不满足则认为成绩不服从正态分布,若满足则进行以下步骤。
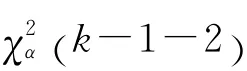
4 实例分析
随机在某学校抽取了某年级某学期的多媒体技术基础试卷,具体成绩数据见表1。对其成绩分布进行正态性检验。
(1)计算样本的均值和方差
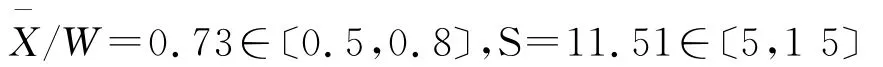
结果满足条件ⅠⅡ,可进行χ2的拟合优度性检验。
(2)假设H :成绩总体Χ服从正态分布;H :成绩总体Χ不服从正态分布。其成绩分组与2计算结果见表2。
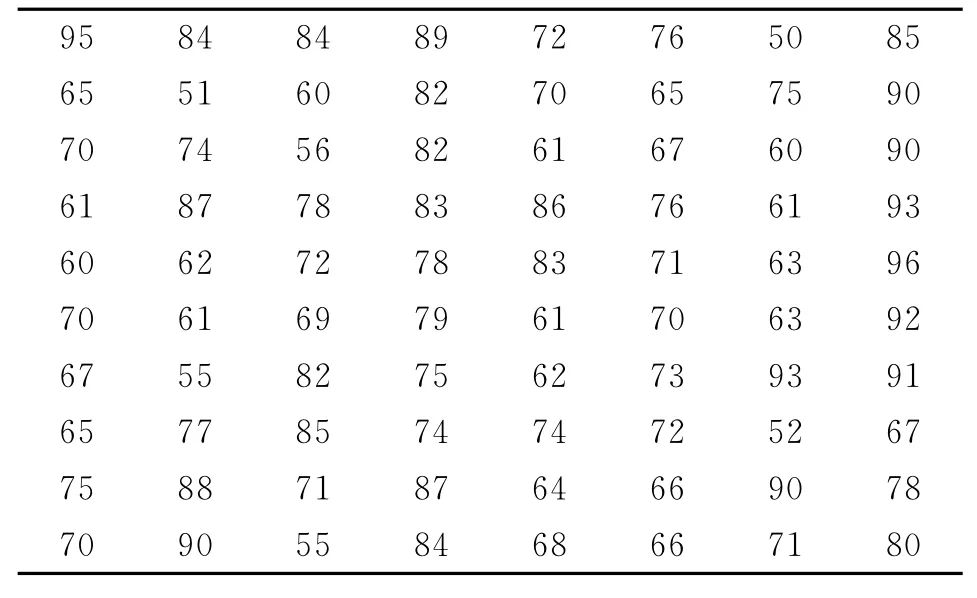
表1 学生成绩表
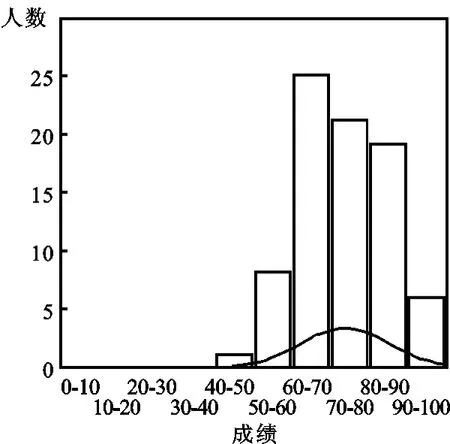
图2 成绩分布直方图
说明:表2的第5栏是各组实上限对应的左尾部面积比例,根据相应的标准分Z查正态布表所得。表2的第6栏是从最低组算起,0.0212直接来自第5栏,其他值由第5栏中上下相邻两组的表值相减得到。
(3)根据原始数据的统计作频数直方图如图2。
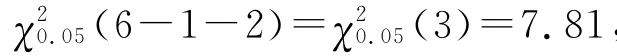
经由步骤(1)(2)(3)(4)知,这次多媒体技术基础的成绩服从“成绩正态分布”。它反映了本期的教学活动正常,教学措施有力,正确地贯彻了该课程教学大纲和教学基本要求,认真进行课堂教学,教学效果较好。
[1]王孝玲.教育测量学[M].上海:华东师范大学出版社,2001.
[2]张志英.教育统计学[M].北京:中国财经经济出版社,2002.
[3][美]M.R斯皮格尔,J.希勒,R.A.斯里尼瓦桑.概率与统计[M].2版.孙山泽,等译.北京:科学出版社,2002.
[4][美]斯皮格尔(Spiegel,M.R),等.统计学[M].3版.杨记龙,等译.北京:科学出版社,2002.
