数学教育哲学是什么——从一则隐喻谈起

魏 佳，罗萍萍

（赣南师范学院，江西赣州 341000）

“数学教育哲学是什么”？与数学教育直接或间接相关的人似乎都能提出这个问题。这是一个最基本的、却又难以直接定义的问题。从数学教育哲学自身的发展进程来看，现已不断涉及对“数学教育哲学是什么”这一问题的追问；另外，由于每个人的哲学观不同，对数学教育哲学的理解就不同，于是导致了多种多样的回答，逐渐引起人们的兴趣和关注。

在数学教育的历史上，不乏对数学教育进行的哲学思考。因为任何一种数学教育观念，或者是在一定的哲学思想之下的直接产物，或者间接反映了某种哲学思想。数学教育哲学作为一种专业化的研究，是在20世纪末开始的，其标志是英国数学哲学家Ernest于1991年出版的《The Philosophy of Mathematics Education》，进一步奠定了数学教育哲学的系统研究。Emest认为对于数学教育哲学的研究应围绕数学教育活动本身，即“数学的本质、数学学习活动的本质、数学教育的目的、数学教育活动的本质”来展开。［1］在我国，南京大学的郑毓信教授率先对数学教育进行了哲学思考，并致力于为数学教育奠定哲学理论基础。他指出：“数学教育哲学的兴起是数学教育现代发展的必然趋势，因为，在经历了种种的‘改革运动’以后……为了更好地解决数学教育何去何从的问题，人们无疑需要从理论的高度对数学教育的一些基本问题做出更为自觉的分析与反思。”［2］此外，还有许多国内外学者都对“数学教育哲学是什么”进行了探讨，并形成了一定的理论基础，而对于这个问题是否存在一种普遍接受的、公认的答案，又成为另外一个论题。

数学教育哲学应该有自己特殊的、相对稳定的研究内容，它不能仅等同于数学教育主体的日常哲学理解或反思；同时，它又应当是一种哲学，而不是什么别的理论，从而也不应把一些不具有哲学意义的论题包括进去。数学教育哲学的研究应从何谈起，根据其发展历程来看，数学教育哲学能够以一中心引发不同答案的方式，即以许多主要问题的讨论为发射中心逐步构建数学教育哲学模式。每一个被提出的有趣问题都存在一个完全不同的视角，从而说明了数学教育哲学中其他系列的重要问题。为了能以第一直觉展示这些不同的视角，本文将通过一个隐喻透视数学教育哲学的诸多研究视角，隐喻故事发展如下。

一、一则隐喻

某日，某公司通知公司全体职员前往208号楼召开会议。公司发令者（我们称之为教师）将提前向其他职员（我们称之为学生）讲述：如何从公司所在位置101号楼（作为起点），到达208号楼（作为终点）。所有职员得到一系列前往208号楼的指令后开始行动，寻找目的地：有些人按指令直接到达了目的地，有些人找错了地方，有些人完全迷路了，有些人跑到“野外”去了，有趣的是竟然有一个人在没有听从指令的情况下，也找到了208号楼（见图1）。

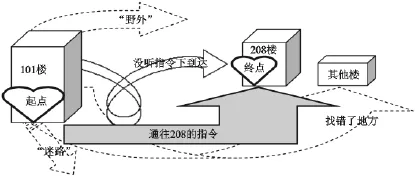
图1

让我们一起来分析一下这则隐喻。在这里，我们将其类比为数学教育现象，尝试用不同的哲学观对其进行“自下而上”的分析，以此来类比研究教师与学生活动中的某些具体关系。从某个哲学视角出发，我们很可能提出以下问题：

1.教师具有怎样的哲学观？哲学观是如何促使他作出指令的？

2.良好的道路指令是怎样的？

3.学生是怎样理解教师的指令的？学生不同的文化背景起到什么作用？简言之，学生具有怎样的哲学观？

图2

换一个哲学视角，如果我们以使“内隐知识外显化”的方式回答这些问题，就会引出以下两个问题：

（1）真的存在一些使“内隐知识外显化”的方式吗？如果存在，那么教师是如何选择恰当的教学方法来发布指令的？

（2）观念是否能帮助教师和学生更加清楚地了解任务的内在背景？（见图2）

如果以上的分析仍不足以说清楚，还可以尝试另一种方式：看看问题中的指令与实际情况之间的关系。从这个哲学视角出发，又派生出一系列不同的问题：

（1）在101号楼和208号楼之间确实有一条路吗？或者，它们之间可能有许多条路，那么我们能否简单地选择一条特定的路而不考虑其他可能性？

（2）在101号楼和208号楼之间根本没有路可走。在某种程度上，这些指令只是相当于一张邀请函：请大家走到外面，创造一条路。这里又引发一个次要问题——我们要建造哪条路，如何建造。

隐喻故事中大部分讨论的假设都与“结构主义观”（道路指令中的语言是该问题的理论集）和或多或少激进的“建构主义观”（道路是人们在野外游玩时集体创造的）有关。然而我们不纠结于这个问题。

到目前为止，一直还没有人质疑“为什么我们都要去208号楼？”这个问题。从这个哲学视角出发，又引发一系列新的“大”问题：

（1）为什么我们都应该知道208号楼在哪？

（2）是谁提出了这个任务，进而引发了探寻之路？

（3）对于少数、多数或全部的学生来说，还可以借助其他哪些建筑物来到达208号楼？

这些问题还可能将我们引入数学教育中有关社会问题的哲学，甚至对它进行公开批判。最后，你可能会惊讶——为什么我们突然之间变得如此具有批判性？

从这个隐喻中，我们可以得出以下结论：

（1）从上述提到的所有视角来看，每种哲学观在进行问题分析时所起的作用是截然不同的，同样适用于分析“数学教育哲学是什么”这一复杂的问题。

（2）数学教育哲学的思考可以“分工”吗？比如，对 “208号楼是否存在”和“指令的质量”的质疑之间是否有联系？数学教育哲学中所有问题都具联接性的观点是令人欢喜的，但却常常无法实施。

（3）如果考虑到问题的另一层复杂性，则要考虑以下问题：假设一位哲学家在某种程度上成功地证实了208号楼根本不存在，那么101号楼里那个可怜的发令者应该怎么做呢？“如果能回答这个问题，那么将有一个大难题被历史性地解决。”（Jean Paul van Bendegen在ICME-10上发表的演讲）

系统地看这则隐喻，在理论上可以说，所提出的不同问题都受到哲学观的影响。随着时代的发展，人们对数学教育的认识和要求发生了变化，用于指导数学教育的哲学思想也有所不同。仅就西方传统的数学教育观念而言，就有所谓严格训导派、技术实用主义、旧人文主义、进步教育派和大众教育派等众多派别，他们对数学教育本质和活动有着不同的见解，代表了各自所持有的不同的哲学立场。像上述隐喻中所涉及的数学教育哲学的中心问题也被不同的派别以众多不同的方式予以回答，每种方式可能都非常生动、有趣。总体上归纳而言，数学教育哲学将受到哲学、数学哲学、教育哲学的影响，并在某种程度上指引人们从这三个视角对数学教育哲学是什么进行回答，这将逐步建构出较为清晰的数学教育哲学的分析框架。

二、哲学、数学哲学、教育哲学的影响

根据Stephen Brown关于数学教育哲学提出的三分法，数学教育界掀起了关于哲学、数学哲学、教育哲学对数学教育的影响的探究。核心问题是：数学教育哲学“是将哲学运用于数学教育，还是它就是数学教育哲学？是将数学哲学运用于数学教育还是一般的教育？是将教育哲学运用到数学教育？”我们用一个图来阐述其中所隐含的关系（见图3）。这三条线索中的任何一条都代表着不同的观点，也将产生不同的争议和问题。但是，我们的目的并不是调查所有的可能性，而是为了将那些在讨论中占主导地位的争议具体化，并尝试揭示它们之间的关系。

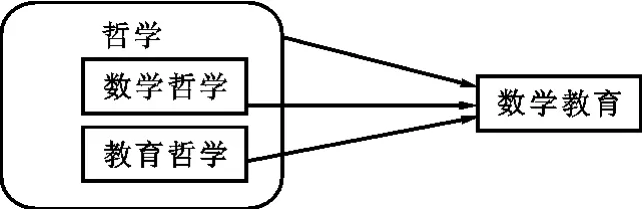
图3

（一）哲学对数学教育的影响

数学教育问题最终都是哲学问题，它应遵循对基础问题的系统分析和严格检验。对数学教育的研究必须上升到哲学的高度，具体地包括与数学教育相关的世界观与方法论，特别是对学生思维、智力、推理、信念和评价的研究。更基本的，还将还原数学教育的本质的探究：数学是什么？数学教育是什么？数学教育的本质是什么？数学与人类的经验是什么关系？这些看似纯理论的问题，对于数学教育来说却是很实际、很重要的，因为它们直接关系到教师和学生的教与学的过程和行为，从而形成不同的观念。例如，数学是一种永恒不变、毋庸置疑的真理？还是从人类社会实践中总结创造出来的知识？这种对数学的哲学思考将直接影响到数学课程的设计和教师的教学方法，隐性的观念传递到学生身上，学生也必然会采用相应的学习方法。哲学对数学教育的作用已指向数学上有关期望效应的标准性问题。［3］例如，培养学生解决问题的辩证思维能力，以哲学理论加深学生对数学概念的哲学理解，在认识概念时获取对概念的哲学价值取向，树立正确的数学教学观，激活人文主义思想，健全学生的个性品质等。要善于用哲学的观点和方法组织数学教学，教会学生用运动观点理解数学知识，使学生树立辩证思维方式，掌握正确解决问题的方法。甚至于，为了解决新课程改革中的种种矛盾，也必须根本地保持“在对立统一中寻找数学教育法则”的平衡。在这些探讨中，一个过分简单的反对派常常出现在数学的“绝对主义者”或“易犯错误者”之间。哲学对数学教育的影响不仅仅是将一些简单的哲学图片描述成有数学教育性质的呈现或加以一些多面的解释。［4］

数学教育实践在哲学指导下所进行的探索提高了哲学本身在数学教育中的地位。许多数学教育哲学的支持者已经总结出经验，即改变数学课堂中的教学实践不仅仅是新课程或资源供应的事情，同时教师个人的传统哲学观念也将会受到挑战，由此可以想象个人哲学观念对课堂实践的重要性，同时也是哲学反思在教师教育课程中变得越来越重要的原因。［5］从科学认识论的观点看，任何知识的获得都要经历一个从具体到抽象、从感性到理性的发展阶段，并且每个人的抽象概括能力总是随着发展规律逐步形成的。因此，教师持有科学的哲学观将帮助学生增长知识，使学生获得不同层次的训练。

除了这些之外，如果我们认识到内隐哲学的影响力的话，那么数学教育最重要的策略之一就是使“内隐知识外显化”。这种思想也是本文的主导思想之一，即使个人内部隐性知识显性化，这样他才能与他人进行有力的交流、沟通，才能引发他人对问题的各方面思考。这一思想并不局限于教师数学课程设计或课程改革的专业讨论，进一步地，它应该运用到课堂中，强调教师的组织性和协调性。只有引导学生对与数学有关的哲学核心问题进行反思时，才能使他们更好地构造数学知识结构，逐步形成科学的思维方式和思维习惯，进而发展各种应用能力。

（二）数学哲学对数学教育的影响

数学教育的发展与数学性质的探究分不开，如数学家创造的方法与美学、数学史在数学教育中的作用与数学教育的紧密联系等，最直观地表现为课程标准的制定者和教材的编写者凭借这种方式传播他们的数学观念。正如Thom，R.所说：“即便数学教学法之间几乎不相干，但它们都以数学哲学为基础。”［6］这种观点是研究数学观对数学教学影响的经典开端。Steiner也从另一个方向强调它们之间的关系，即每种数学哲学都包含数学教学实践中隐含的意义。［7］数学方法是构建哲学体系的重要方法之一，数学教育哲学离不开数学哲学的影响。

数学哲学对数学教育的影响特别强调数学的学科特性。徐利治对数学哲学从数学本体论、数学认识论、数学方法论出发进行分析，这三论具体地体现了数学教育与数学哲学、数学史之间的密切联系。［8］更重要的是，由于数学模式是确定的、特定的客观内容，而这种内容又不可能借助于真实世界的联系获得直接简单的说明，因此这些模式构成另一类与真实世界互不相同的独立存在。数学这种思维的逻辑性与抽象性，决定了数学教育的指导方向。例如，数学认识论对数学教育的价值最重要的作用在于阐述了数学教育的特殊性——数学是通过模式建构、以模式为直接对象，从事客观实体量性、规律性研究的科学。

数学教育实践中，数学哲学具有确定的影响力。一些常见问题如：怎样解决数学问题、怎样发现数学原理和创造数学问题解决的方法，学生如何理解概念、掌握方法、解决实际问题，甚至是如何切身体会数学的美、感受数学家对数学的情感等，都离不开这种数学工具。特别地，徐利治对数学方法论的分析包括：归纳法和类比法，抽象分析法和倒推分析法，尝试法，一般解题方法。［8］不难发现，其中的任何一种方法在数学教育中都有着广泛的应用。

除数学哲学这种主要受学科性质影响的哲学观外，教师本人持有的数学哲学观对他的教学方式也有很大影响。一项著名的研究结果表明：教师数学专业思想的形成与他们所表达的数学内容的典型性之间存在着一致性，这有力地说明了教师的数学观、数学信仰和爱好的确影响着他们的教学活动。［9］

然而，数学教育的理解难道可以仅仅局限于数学哲学方面？数学教育哲学仅仅是数学哲学问题？数学哲学占据什么样的地位？数学哲学性质如何转化为学校教育目标，它对数学的教与学有什么作用？……Brown主张不要将数学教育哲学的讨论仅仅局限在数学哲学方面。［10］如果我们将哲学理解为反思性学科对数学教育所产生的影响的话，那么这一领域便开始扩大，一些问题将会不断涌现，如数学与社会有什么关系？数学，教师应该教什么？学生应该学什么？数学教育在知识领域中的地位如何？

（三）教育哲学对数学教育的影响

教育哲学的基本问题包括教育本质、教育价值、教育目的、知识与教学、道德与美学等。教育哲学强调教育、社会与人三者之间的关系；讨论人的价值和主体性在教育中的体现；分析马克思关于人的全面发展学说与教育目的制定之间的关系；探讨教学论及其发展规律；传授传统道德经验和探讨美育的任务等。教育哲学的要求和理论直接影响到数学教育的发展。从教育哲学角度对数学教育进行分析，我们可以得到有关数学这样的定义：如果数学教育旨在使人能对数学进行批判性地反思，那么数学教育应提供让普通人进行评论的数学。因此，数学必须包含目标和目的以及意义和含义，而这些都是哲学课程的核心思想，被称作普通数学。［11］

对于数学教育工作者来说，教育哲学不是可有可无的，而是不可缺少的，包括对教育问题进行哲学的思考，从哲学的视角对教育中的问题和现象进行深入本质的分析研究等，以促进教育实践者的自我反思和理性自觉。任何一位数学教育工作者在对“好”的数学教育进行价值判断时，都必须关切教育制度、教育形式和教育活动，通过理性思考建构起关于数学教育的较为系统的、理论化的个人基本观念体系。这样，不仅有助于教师自身的发展，还有助于培养学生的人文素质，同时还将推动教育改革。

教育哲学的主题随时代变迁而不断转换，追寻这一轨迹，我们可以看到数学教育也紧随这些哲学家、思想家的脚步及时调整步伐。在当代教育世界里，人在功利主义价值导向下正在全面地失去自然，学校教育学科分割、知识与能力分裂脱节，这些正使我们下一代的成长经验受到压抑和宰割；另外，当代学校教育体制急剧膨胀正成为人类教育的主导形式，而家庭和社会教育日益弱化。于是，尊重多样、发展个性、鼓励多元等成为教育哲学的又一话题。教育哲学的要求和理论直接影响到数学教育的发展。如《进入21世纪的中小学数学教育行动纲领》（以下简称《行动纲领》）是上海迈向新世纪，以建设一流教育理念为先导的计划纲要。考虑到上海的现代化建设需要更多、更有用的数学，于是在《行动纲领》中提出以“学生发展”为21世纪数学教育改革行动的口号，具有鲜明的时代特点。

在教育哲学对数学教育产生影响的同时，反过来数学教育对教育哲学也将产生影响，两者之间相互作用。反思数学教［12］——即数学教育的目的主要是通过批判学生数学使用的能力和批判数学教育的“权利格式化”来实现。因此，强调学生应该更多地参与到注重应用的数学课型中。

三、反思

数学教育哲学是什么？对这一问题的探讨还没有或许永远不会停止。Stephen Brown的三分法选取了几个主要的论题搭建了数学教育哲学的分析框架，是现在主要盛行的分析思路。对此，现代的哲学家和思想家更多地采取了相对主义立场，即采取反对绝对运动和承认相对静止的观点来看哲学、数学哲学、教育哲学与数学教育的关系，从而研究数学教育哲学。哪个才是最重要的观点呢？正如相对主义所持的观点，最基本的一步是先明确所有的观点都有其重要的一面，因此它们是互补的——必须共存共生，互相借鉴与发展，共同刻画数学教育哲学的雏形，哺育其成长。同时，我们也不能否认它们之间存在明显的并行关系（更多地解释为相对独立性）——应关注各派别组织中所提出的重大问题及对数学教育所产生的重大影响。这也是为什么我们一方面要继续相互学习、接纳不同的观点，另一方面又不能轻视讨论中提出的重大问题。在进行数学教育哲学思考时，应注意其多样性与统一性的结合，这样才能与数学教育的本质相符。因此，再次回顾上述隐喻故事，它对应着数学教育哲学的许多中心问题，每一个问题都存在不尽相同的视角，值得我们去思考。

［1］ERNEST P.The Philosophy of Mathematics Education［M］.London：Falmer Press，1991.

［2］郑毓信.数学教育哲学［M］.成都：四川教育出版社，2001.

［3］ERNEST P.Mathematics Education and Philosophy：An international perspective［M］.London：The Falmer Press，1994.

［4］MENEGHETTI R.About possible relations between philosophy of mathematics and philosophy of mathematics education，Contribution for DG 4.2004.

［5］LINDGREN S.Plato's Epistemology and Mathematics Education，Contribution for DG 4.2004.

［6］THOM R.Modern mathematics：does it exist？［J］.Howson，A.Geoffrey（ed.）Developments in Mathematics Education，Proceedings of the2nd ICME，Cambridge University Press，1973.

［7］STEINER H.G.Philosophical and Epistemological Aspects of Mathematics and their Interaction with Theory and Practice in Mathematics Education［J］.For the Learning of Mathematics 1987，7（1）.

［8］徐利治.徐利治谈数学哲学［M］.大连：大连理工大学出版社，2008.

［9］Davis P J.Fidelity in Mathematical Discourse：Is One and One Really Two？［J］.American Mathematical Monthly，1972，79（3）.

［10］BROWN S I.Philosophy of Mathematics Education：POM（E），PO（ME）OR POE（M）？［J］.Philosophy Of Mathematics Education Newsletter.1995（8）.

［11］LENGNINK K，PREDIGER S，SIEBEL F.Mathematik und Mensch.Sichtweisen der Allgemeinen Mathematik［J］.Verlag Allgemeine Wissenschaften，Mühltal，2001.

［12］SKOVSMOSE O.owards a philosophy of critical mathematics education，Kluwer，Dordrecht，1994.