基于高频数据沪深300股指期货量价关系研究＊

张小勇，任德平，2

（1.湖南大学 工商管理学院，湖南 长沙 410072； 2.长沙理工大学 经济与管理学院，湖南 长沙 410114）

一 引 言

由于量价关系是股票技术分析理论的重要基石，也是广大投资者在投资实践中判断市场或个股运行趋势的主要手段之一，因此，量价关系研究一直以来是金融学领域的研究热点之一。

早在1970年，Crouch［1］发现无论指数还是个股，其绝对价格收益与交易量呈现同期正相关关系。Karpoff［2］研究发现成交量与股票绝对收益率变化呈现一种正相关关系。Gallant等［3］进一步证实了该结论。国内的陈怡玲和宋逢明［4］对中国股市实证发现日交易量与日绝对价格变化之间也存在线性正相关关系。后来有很多学者试图从各个角度对这一正向相关关系加以解释，但始终没有得出一个统一的结论。Clark［5］提出了混合分布假说，认为市场一种潜在不可观察的信息流是导致交易量和价格波动变化的共同驱动因素。Copeland［6］提出了连续信息到达假说，认为市场信息逐步向外扩散导致了价格波动和交易量同步扩大。Harris和Raviv［7］构建了“判断差异模型”，认为投资者对市场同一信息的判断偏差导致了交易的发生，股价绝对变化与成交量表现出正相关关系。Wang［8］建立了“理性预期资产定价模型”，认为投资者之间拥有的私人信息和投资机会不对称导致了成交量与价格变化的正相关。

尽管如此，上述研究主要集中价格变化与成交量的同期相关上，对量价关系背后的驱动因素没做深入探讨。为了更深入地研究交易量与价格波动之间的关系，许多学者从更微观的角度去探究量价关系背后的主要驱动因子。Kyle［9］研究了知情交易者的订单流非平衡（order imbalance）对价格波动的影响。Jone等［10］将交易量分解成成交次数和平均交易头寸来考察不同交易量成分对股价波动的影响，结果发现成交次数解释了大部分股价波动率。Huang 和Masulis［11］使用伦敦交易所的数据进一步证实了他们的结论。Chan 和Fong［12］证实了订单流非平衡可以解释一部分股票收益，而且过滤订单流非平衡的成交次数对股价波动率影响很小，因此推断订单流非平衡可能是量价关系主要驱动因子。Easley等［13］研究发现知情交易者更倾向于大额订单交易，因此，认为交易头寸可能包含更多价格信息。为了避免隐藏信息在市场提前暴露，知情交易者往往倾向于将隐藏信息通过大额交易拆分成许多小额交易的渠道来在市场上逐步释放。Chakravarty［14］进一步证实了隐藏交易假设的存在，认为订单流非平衡、成交次数包含更为丰富的股票价格信息。Chan和Fong［15］用高频已实现波动率代替绝对价格收益来研究量价关系背后的驱动因子，结果发现成交次数能够对量价关系形成有力解释，交易头寸和订单流非平衡对量价关系的解释力有限。Giot等［16］实证了连续样本路径方差和跳跃方差分别与交易量、交易头寸、成交次数和订单流非平衡之间的相关关系。Chevallier和Sevi［17］使用能源期货市场日内高频数据考察了已实现波动率及其衍生波动率与交易量、成交次数和交易头寸之间的相关关系。

国内对量价关系的研究主要集中在相关性检验和因果分析上，张维、闫冀楠［18］采用Granger因果检验实证了上证指数，结果发现周收益对交易量具有明显的线性因果关系，但交易量对收益率不具有线性因果关系。随后，陈良东［19］利用因果检验和回归分析对上证股市进行实证研究，结果显示交易量与价格绝对变化存在显著的正相关关系。王承炜等［20］实证发现沪深两市都存在价格收益对交易量的的线性因果关系和双向非线性因果关系。王杉、宋逢明［21］建立了简单的量价关系模型进行实证，发现非知情交易者持仓量的变化和预期变化对量价关系有重要影响。梁丽珍［22］利用分量回归法来分析中国股市的量价关系，结果发现中国股市具有“价量齐扬”和“价跌量缩”的现象。随着金融高频数据应用的逐步推广，有的学者开始尝试利用高频数据来对量价关系进行研究。李梦玄、周义［23］使用沪深两市高频5 分钟指数数据对量价关系进行了实证研究，结果表明两市量价之间仅存在双向线性引导关系，并不存在非线性Granger因果关系。郭梁、周炜星［24］通过高频数据研究了中国股市个股的成交量与价格变化之间的关系，实证研究发现中国股市成交价格波动与成交量之间具有相关关系，量价关系曲线为一非线性凸函数。

综合以上研究分析，国内学者主要集中在对中国股市交易量与价格波动之间正相关关系的检验和因果分析上，且多数停留在宏观层面上的简略分析，对量价关系背后的驱动因子的探索研究几乎没有，此外，鲜有学者对股指期货市场的量价关系做出研究。因此，本文在MDH 理论的基础上，以沪深300股指期货为研究对象，通过建立相应的线性模型并结合沪深300股指期货的高频数据进行实证分析，以求能够综合全面地揭示我国期指市场量价之间的规律性特征。

二 研究方法介绍

（一）量价关系模型的建立

本文将通过建立简单的线性模型来考察沪深300股指期货的量价关系的变化，即以波动率作为被解释变量和以交易量和其他影响因子作为解释变量构建多元线性回归模型来进行研究。为了综合考察沪深300股指期货的量价关系，本文将从基本量价关系、连续和跳跃波动的量价关系以及量价关系非对称性等三方面来建立相应的线性模型进行研究。

（1）量价关系基础模型

Chan 和Fong［15］研究发现已实现波动率代替绝对收益作为波动率的精确估计量可以更好地刻画交易量与价格波动之间的关系。因此，本文将选取已实现波动率作为沪深300股指期货价格波动率的有效估计量。由于我国股指期货合约交割日为合约到期月的第三个星期五，其价格波动往往随着期指临近到期而变得日趋剧烈，同时也为了考虑周末效应对期指波动的影响，引进虚拟变量DUMMYt，Friday。另外，已实现波动率往往存在很强的自相关性，故在模型中将已实现波动率的滞后期考虑进来。基于以上分析，构建如下线性模型：

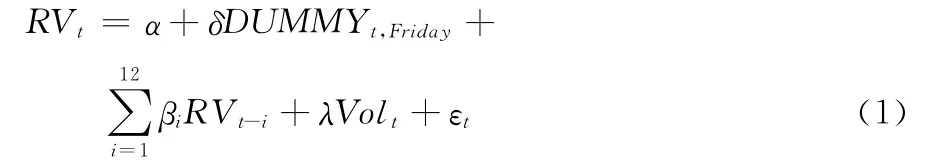
模型（1）是本文构建最基础的量价关系模型，其中：RVt表示第t天所对应的已实现波动率，即：为第t天所对应的成交量。

为了进一步深入研究沪深300股指期货之间的量价关系，以找出量价关系中最主要的驱动因素。我们根据Jones等［10］的研究将日成交量分解为日成交次数和平均交易头寸，在模型（1）的基础上都建了如下模型：

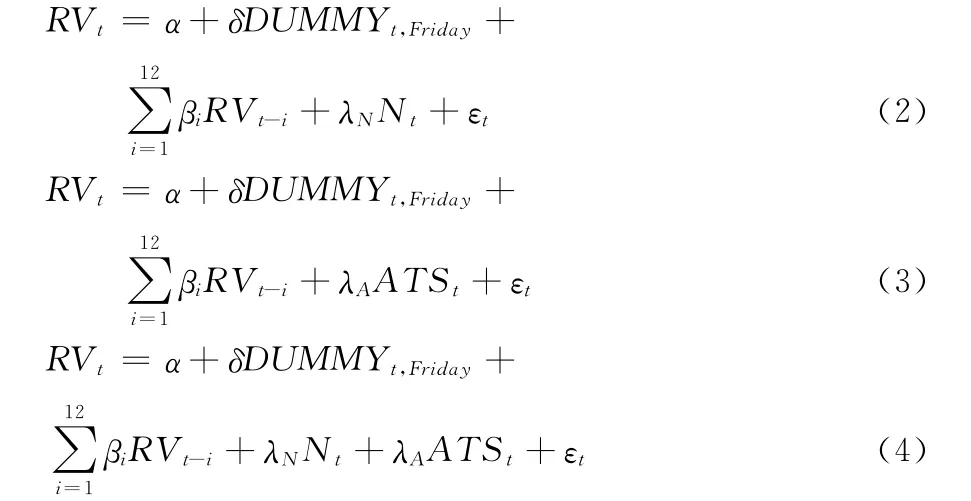
其中：Nt为第t天的成交次数，ATSt为第t天的平均交易头寸（日成交总量除以成交次数），即

（2）连续和跳跃波动量价关系模型

Andersen和Bollerslev等［25］基于二次变差理论将已实现波动率分解成连续样本路径方差和跳跃方差。为了考察成交量对已实现波动率中连续样本路径方差和跳跃方差的影响，我们仿效Giot等［16］的建模原理，构建了如下模型：

（3）量价关系非对称性模型

为了对资产价格下降时的风险进行准确度量，BNKS（2008）［26］针对已实现波动率提出了上偏已实现半方差（RS＋t）和下偏已实现半方差（RS－t）。Chevallier和Sevi［17］将它们应用到量价关系的非对称研究上。为了检验沪深300股指期货量价关系的非对称性，我们参照Chevallier 和Sevi［17］的研究成果，建立了如下模型：

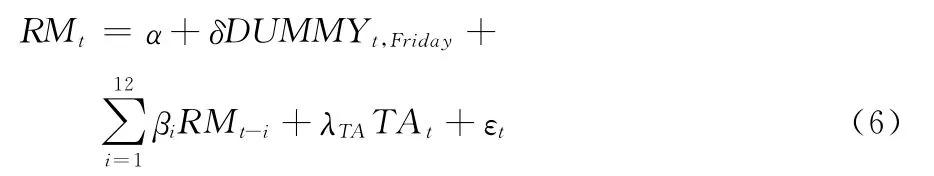
其中：RM＝｛RSt＋，RSt－｝，TA＝｛Volt，Nt，ATSt｝，RV＝RSt＋＋RS－，RSt＋、RSt－分别表示上偏已实现半方差和下偏已实现半方差，即：。对模型（6）的估计，我们仍将采用类似于模型（5）的估计原理，即：对RS＋t和RS－t分别按照（1）—（4）式进行估计，然后从总体上对沪深300股指期货的量价关系的非对称性进行准确判断。

考虑到以上量价关系线性模型估计结果的残差可能存在自相关或异方差性，为了提高模型的估计精度，本文除了跳跃波动以外都将采用OLS with Newey west估计法进行参数估计，对跳跃波动量价关系模型将仿效Giot等［16］采取TOBIT 回归进行估计。然后，分别对各量价关系模型的估计结果进行细致分析，最后从总体上对沪深300股指期货的量价关系进行归纳总结。

（二）跳跃方差的分离

由于上述量价关系的线性模型涉及到已实现波动率中跳跃方差，因此，我们有必要对已实现波动率中跳跃方差的分离原理做出简单的说明。跳跃方差实际上为已实现波动率与跳跃稳健估计量之差，为了提高跳跃方差的分离有效性，我们还需要通过相应的统计量对显著的跳跃波动进行检验。

首先，对于一个服从连续跳跃离散过程的资产对数价格，我们将其样本期内t日离散时间区间的日内收益率定义为：rt，j＝pt，j－pt，j－1。根据Andersen和Bollerslev［27］对已实现波动率的定义，我们可知第t日的已实现波动率为RVt＝（M为日取样次数）。

其次，Barndorff－Nielsen和Shephard［28］，［29］考虑市场存在有限次跳跃波动的情况下而提出了“已实现”双幂次变差（Realized Bipower Variation，RBV），它可以作为已实现波动率中的跳跃成分的稳健估计量。

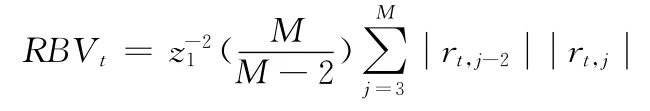
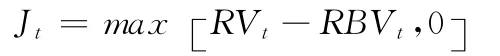
再次，为了提高跳跃波动的估计精度，我们采用Huang和Tauchen［30］提出一个渐近服从标准正态分布的Zt统计量来对显著性跳跃性波动进行检验。即：

Andersen等［31］提出了一种全新的估计量MedRV 来代替RBV 作为估计跳跃波动的稳健估计量可以明显提高检验显著跳跃性方差的有效性。即：

相应的，Zt统计量中的RTQt将由MedRTQt来代替。即：

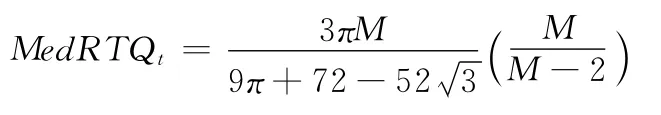
通过对Zt统计量的计算，在1－α的显著性的水平下（α＝99%），我们得到离散跳跃方差的估计量：

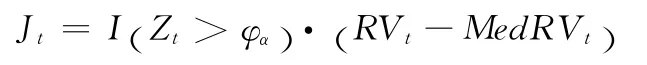
连续样本路径方差估计量：

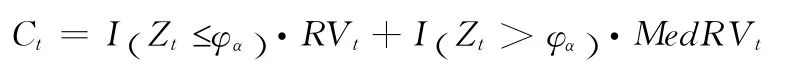
三 实证分析

（一）样本数据获取及基本分析

本文以沪深300股指期货当月连续指数为实证样本对象，选取样本期2011年4月11日至2012年4月10日共计244个交易日的5分钟高频数据进行实证分析。由于沪深300股指期货的交易时间为上午9：15－11：30，下午13：00－15：15，交易时长为4个半小时，比股市多出半个小时，因此，我们剔除交易时间外的数据还剩下13140个有效数据，平均每天约为54个数据。选取的样本指标为交易时间、收盘价、成交量及成交次数，数据来源于同花顺行情分析软件。

表1记录了沪深300股指期货各实证统计量描述性统计特征的相关数据。通过分析，已实现半方差的均值（RS＋和RS－）为已实现波动率的一半，且上偏已实现半方差的均值要约大于下偏已实现半方差的均值，这说明沪深300股指期货市场期指价格上涨的风险要高于价格下跌的风险，也间接反映市场的投资者的交易策略倾向于做多，对市场做空相对谨慎。另外，已实现波动率中的连续成分所占比约为72.8%，这说明了连续波动成分相对跳跃波动成分在已实现波动率中占据主导地位。除跳跃波动以外，各统计量在滞后12阶仍具有很强的自相关性，因此，针对各量价关系模型中考虑滞后变量的相关性影响的建模分析具有一定的统计基础。

表2给出了沪深300股指期货各统计量之间的相关系数，我们发现已实现波动率与成交量表现出明显的正相关关系，即期指波动随着成交量的放大而不断加剧，这与国内外量价关系正相关性的结论相一致。成交量（Vol）与平均交易头寸（ATS）的很高的相关性强度，且它们之间的相关系数要明显高于成交量（Vol）与成交次数（Num）的相关系数，这说明交易头寸与成交量包含大量类似的市场信息成分，此外，已实现波动率（RV）与平均交易头寸（ATS）也表现出很强的相关性，这与Chan和Fong［15］及Giot等［16］研究的结论截然相反。沪深300股指期货的已实现半方差与平均交易头寸（ATS）保持很强的正相关关系，有别于Chevallier和Sevi［17］在能源期货上研究发现的负相关关系，且上偏已实现半方差（RS＋）与成交量（Vol）之间的相关系数要明显高于下偏已实现半方差（RS－）与成交量（Vol）之间的相关系数，但都与成交量保持正向的相关关系。相比跳跃波动成分下微弱的量价相关性，连续波动成分与成交量之间拥有更强的相关关系。

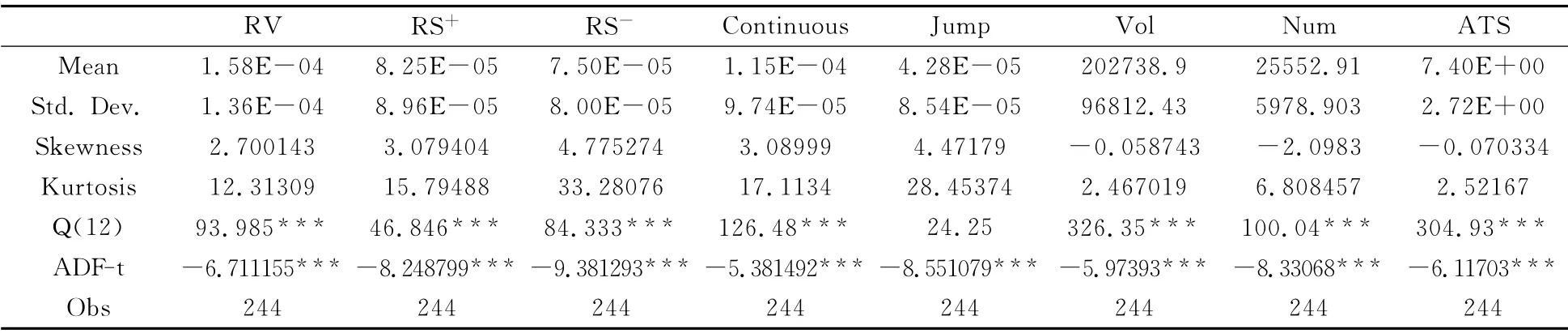
表1 沪深300股指期货各指标描述性统计分析

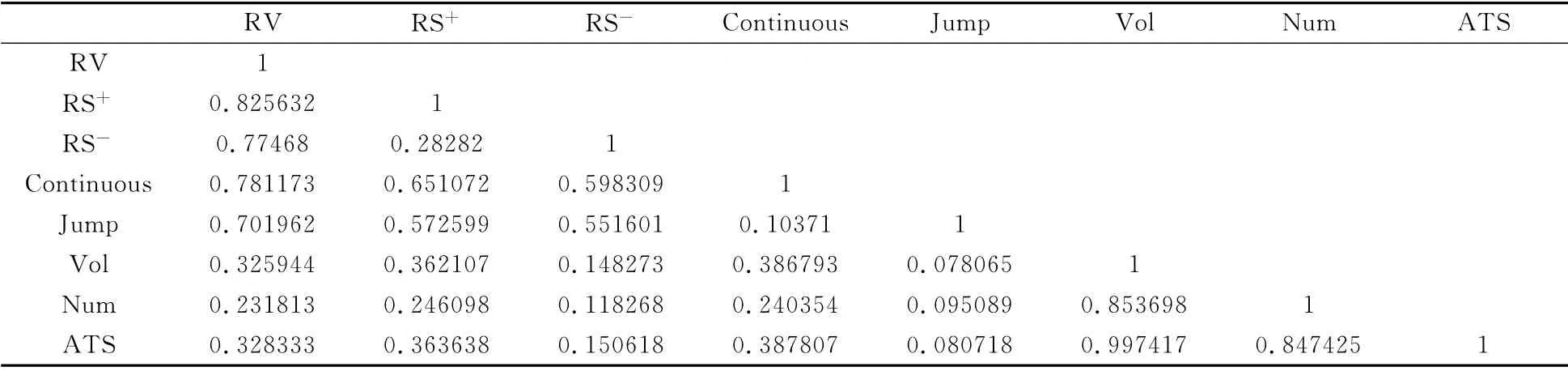
表2 沪深300股指期货各统计量相关系数矩阵

（二）量价关系模型的估计及分析

在上述各统计量描述性特征及相关性分析的基础上，我们对沪深300股指期货的量价关系进行了初步论证。为了进一步探究我国沪深300股指期货市场的量价关系内在表现形式，以便我们挖掘出隐藏在量价关系背后的驱动因子及相关动态特征，我们将分别对文中建立的量价关系基础模型、连续和跳跃波动量价关系模型及量价关系非对称模型进行实证参数估计，并结合实际市场情况加以分析。

关于未来，马国新说：“我没有什么豪言壮语，也不表什么决心，我只要扎扎实实的干好本职工作，无愧于党和人民，这就足够了。”

1.量价关系基础模型估计

表3记录了量价关系基础模型主要变量的参数估计结果，我们发现反映“周末效应”影响效应Dum 所对应系数在1%的显著性水平下都不显著，这说明“周末效应”对沪深300股指期货的量价关系没有形成明显的影响。从RV－model（1）来看，成交量对已实现波动率存在显著的正向影响，这说明市场波动伴随成交量的放大而加剧，伴随成交量的萎缩而减弱，即沪深300股指期货市场呈现“价量齐涨”和“价量齐跌”的现象。将成交量分解成成交次数和平均交易头寸再进行估计，由RV－model（2）和RV－model（3）参数估计结果来看，成交次数和平均交易头寸都对期指波动存在显著的正向影响，另外，RV－model（3）的Adjusted R2要大于RV－model（2）的Adjusted R2，这说明沪深300股指期货市场的平均交易头寸相比成交次数更好地解释了期指的波动。当成交次数和平均交易头寸同时加入到模型中进行估计时，成交次数前的系数并不显著，Adjusted R2并没有太大提高，从而进一步证实了平均交易头寸在解释期指已实现波动率中扮演着最为重要的角色，是期指量价关系背后的主要驱动因子，这与Giot等［16］在美国股票市场发现量价关系背后的驱动因子是成交次数，而不是平均交易头寸的结论截然相反。这反映了我国期指市场的投资者对市场信息倾向于使用大单交易来做出反应，因而平均交易头寸包含了更多的真实市场信息；而发达国家金融市场投资者的交易行为更符合隐藏交易假说相关理论，即将大单交易拆分成许多小单交易来隐藏市场信息，因此成交次数是量价关系背后驱动因子。

表3 量价关系基本模型的参数估计结果

2.连续和跳跃波动量价关系模型估计

表4和表5分别记录了连续和跳跃波动量价关系主要变量的参数估计情况。经分析我们发现，成交量、成交次数和平均交易头寸对已实现波动率的连续和跳跃成分都有着不同程度的正向影响。基于连续波动构建的量价关系模型参数估计结果在1%的显著性水平下都是显著的，而基于跳跃波动构建的量价关系模型参数估计结果在10%的显著性水平下才显著，这说明相比跳跃波动，连续波动的量价关系较为精确地反映了沪深300股指期货的量价关系，同时也间接反映出连续波动成分包含了更多的已实现波动率的信息成分，因此，我们可以利用连续波动相关历史信息对期指的已实现波动率做出预测。表4中的C－model（1）中的Adjusted R2要高于表3中的RV－model（1）中的Adjusted R2，即剔除跳跃波动后的量价关系模型的拟合优度有了明显改善，这反映了期指的量价关系还受到跳跃波动所带来的噪音影响。另外，结合表4和表5中的模型（2）（3）（4）来分析，我们发现无论是从待估参数大小还是从模型的拟合优度都显示了平均交易头寸做为量价关系背后的关键驱动因子，能够更好地解释连续和跳跃的波动的相关变化。

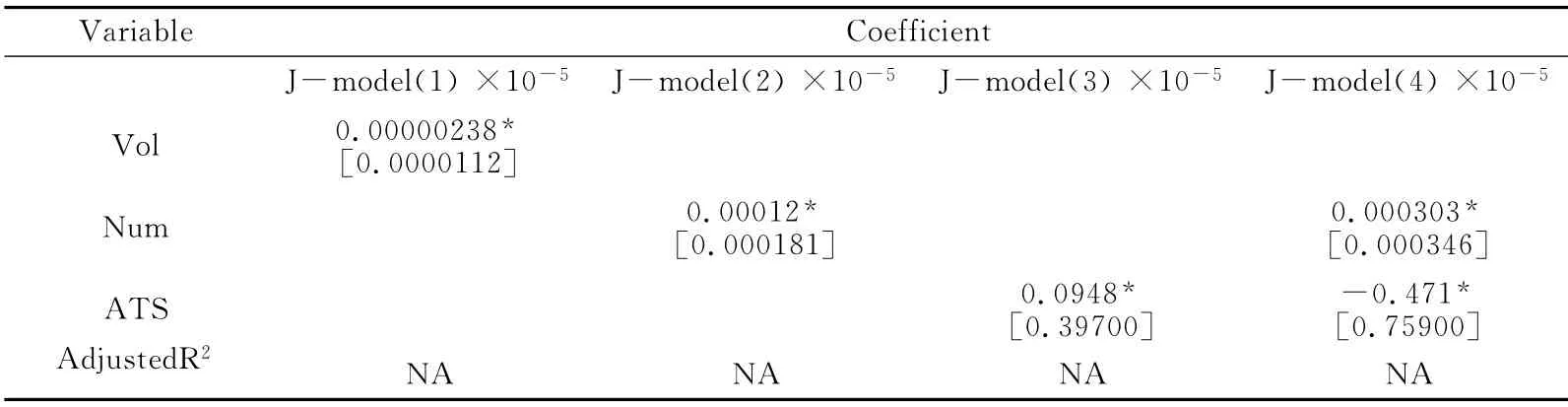
表5 跳跃波动量价关系模型估计结果

3.量价关系非对称模型估计

为了反映沪深300股指期货市场价格上涨和价格下跌量价关系的变化，我们建立了相应的量价关系非对称模型，并利用市场数据对模型进行了估计，结果如表6和表7所示。通过对成交量、成交次数及平均交易头寸三个变量进行单独估计的结果来看，三个变量对上偏已实现半方差和下偏已实现半方差都有着明显的正向影响，但是它们对两者的解释力有着很大的差别。纵观表6和表7所对应的Adjusted R2，下偏已实现半方差量价关系模型的调整拟合优度明显大于上偏已实现半方差量价关系模型的拟合优度，这说明成交量、成交次数及平均交易头寸等变量对下偏已实现半方差的解释程度要高于上偏已实现半方差，也间接反映出下偏已实现半方差相对于上偏已实现半方差包含更多的波动信息，进一步证实了Potton和Sheppard［32］的研究结论，即下偏已实现半方差更适合用于对已实现波动率进行预测。另外，从各模型单独估计情况来看，平均交易头寸相比成交量和成交次数较好地拟合了已实现半方差的量价关系模型，且对已实现半方差的解释程度最高，因此，平均交易头寸实际上为沪深300股指期货量价关系背后的主要驱动因子。

表6 上偏已实现半方差量价关系模型估计结果

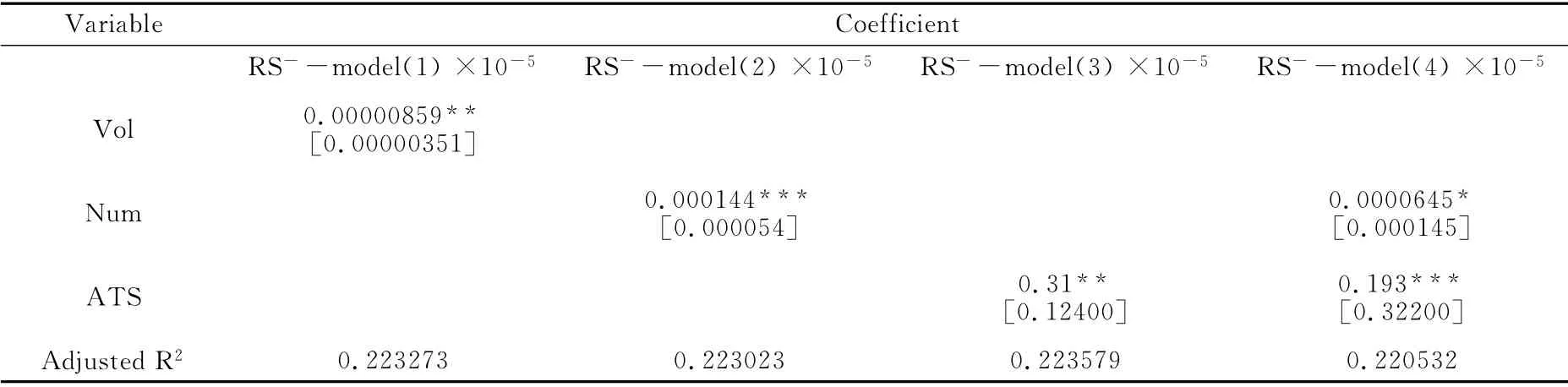
表7 下偏已实现半方差量价关系模型估计结果

四 结 论

（1）与中国股市一样，沪深300股指期货市场成交量与已实现波动率之间表现出明显的正相关关系，即期指的波动伴随着成交量的放大而不断加大，伴随着成交量的缩小而不断减少。成交量、成交次数及平均交易头寸等变量对期指的波动率有着正向的影响，能对市场波动做出一定程度的解释，因此，它们在某种程度上都可以充当市场信息的代理变量。其中，平均交易头寸相对成交量和成交次数而言，能够更大程度地解释期指市场已实现波动率，从而证实了标准的市场微观结构理论，即平均交易头寸包含了更多知情交易者的行为信息，市场波动大部分是知情交易者的买卖行为导致。

（2）沪深300股指期货市场上成交量、成交次数及平均交易头寸等变量对已实现波动率的连续和跳跃波动成分有着显著的正向影响。连续波动成分包含更多价格波动的相关信息，利用连续波动的相关信息可以更为精确地对已实现波动率做出预测。成交量对连续波动的正向影响要明显大于其对跳跃波动率的影响。因此，连续波动与成交量之间的正相关关系可以较为精确地反映沪深300股指期货市场总的量价关系的变化。

（3）沪深300股指期货市场的量价关系存在一定程度的非对称性特征，主要体现在期指价格上涨和下跌过程中的波动信息含量不一样，即下偏已实现半方差较上偏已实现半方差包含更多的已实现波动率信息；成交次数和平均交易头寸的成交量信息含量不一样，即平均交易头寸较成交次数包含更多的市场信息。

（4）通过对三种量价关系模型的实证分析结果，我们发现平均交易头寸比成交量和成交次数更好地拟合了量价关系模型，同时也更好地解释了市场波动的相关信息，因此，平均交易头寸实际为沪深300股指期货市场量价关系背后的主要驱动因子，它可以作为期指市场新信息到达市场的代理变量。

［1］Crouch，R.L.The Volume of Transactions and Price Changes on the New York Stock Exchange［J］.Journal of Financial Analysts，1970，（26）：104－109.

［2］Karpoff，Jonathan M.The relation between Price Changes and Trading Volume：A Survey［J］.Journal of Financial and Quantitative analysis，1987，（1）：109－126.

［3］Gallant，A.R.，Rossi，P.E.，Tauchen，G.Stock prices and volume［J］.Review of Financial Studies，1992，（5）：199－242.

［4］陈怡玲，宋逢明.中国股票市场的价格变动与交易量关系的实证研究［J］.管理科学学报，2000，（2）：62－68.

［5］Clark P K.A Subordinated Stochastic Process Model with Finite Variance for Speculative Price［J］.Journal of Econometric，1973，（1）：135－155.

［6］Copland T E.A Model of Asset Trading under the Assumption of Sequential Information Arrival［J］.Journal of Finance，1976，（9）：1149－1168.

［7］Harris M.，Raviv A.Difference of Opinion Make a Horse Race［J］.Review of Financial Studies，1993，（6）：473－506.

［8］Wang J.A Model of Competitive Stock Trading Volume［J］.Journal of Political Economy，1994，（1）：127－168.

［9］Kyle，A.S.Continuous auctions and insider trading［J］.Journal of Econometrica，1985，（53）：863－894.

［10］Jones C.，Kaul G.，Lipson，M.Transactions，volume and volatility［J］.Review of Financial Studies，1994，（7）：631－651.

［11］Huang R.，Masulis R.Trading activity and stock price volatility：evidence from the London Stock Exchange［J］.Journal of Empirical Finance，2003，（10）：249－269.

［12］Chan，K.，Fong，W.M.Trade size，order imbalance，and the volatility－volume relation［J］.Journal of Financial Economics，2000，（57）：247－273.

［13］Easley D.，Kiefer N.，O’hara M.One day in the life of a very common stock［J］.Review of Financial Studies，1997，（10）：805－835.

［14］Chakravarty S.Stealth－trading：Which traders trades move stock prices？［J］.Journal of Financial Economics，2001，（61）：289－307.

［15］Chan K.，Fong W.Realized volatility and transactions［J］.Journal of Banking and Finance，2006，（30）：2063－2085.

［16］Giot P.，Laurent S.，Petitjean M.Trading activity，realized volatility and jumps［J］.Journal of Empirical Finance，2010，（17）：168－175.

［17］Chevallier J.，Sevi B.On the volatility－volume relationship in energy futures markets using intraday data［R］.Working Paper，2011

［18］张维，闫冀楠.关于上海股票市场价量因果关系的实证探测［J］.系统工程理论与实践，1998，（6）：111－114.

［19］陈良东.上海股市价量关系的实证分析［J］.上海财经大学学报，2000，（3）：37－41.

［20］王承炜，吴冲锋.中国股市价格—交易量的线性及非线性因果关系研究［J］.管理科学学报，2002，（2）：7－12.

［21］王杉，宋逢明.中国股票市场的简单量价关系模型［J］.管理科学学报，2006，（4）：65－72.

［22］梁丽珍.分量回归下的中国股市价量关系研究［J］.统计研究，2008，（12）：73－78.

［23］李梦玄，周义.基于高频数据的中国股市量价关系研究［J］.财经论坛，2009，（3）：132－133.

［24］郭梁，周炜星.基于高频数据的中国股市量价关系研究［J］.管理学报，2010，（8）：1242－1247.

［25］Andersen T.G.，Bollerslev T.，Diebold F.X.Roughing it up：including jump components in the measurement，modeling and forecasting of return volatility［J］.The Review of Economics and Statistics，2007，89：701－720.

［26］Barndorff－Nielsen O.，Kinnevrock S.，Shephard N.Measuringdownside risk—— Realised semivariance［A］.T.Bollerslev，J.Russell and M.Watson（Eds.）Volatility and Time Series Econometrics：Essays in Honor of Robert F.Engle［C］.2008，Oxford University Press.

［27］Andersen T.G，，Tim Bollerslev T.，Diebold F.The distribution of exchange rate volatility［J］.Journal of American Statistical Association，2001，（96）：42－55.

［28］Barndorff－Nielsen O.E.，Shephard N.Power and bipower variation with stochastic volatility and jumps［J］.Journal of Financial Econometrics，2004，（2）：1－37.

［29］Barndorff－Nielsen O.E.Econometrics of testing for jumps in financial economics using bipower variation［J］.Journal of Financial Econometrics，2005，（4）：1－30.

［30］Huang X.，Tauchen G.The relative price contribution of jumps to total price variance［J］.Journal of Financial Econometrics，2005，（3）：456－499.

［31］Anderson T.G.，D.Dobrev，and E.Schaumburg.Jump－robust volatility estimation using nearest neighbor truncation［R］.NBER Working Paper No.15533，2009.

［32］Patton A.，and Shapperd K.Good volatility，bad volatility：signed jumps and the persistence of volatility［R］.Working Paper，2011.