接触式纱线张力传感器动态测量模型

吴震宇，陈琳荣，李子军，叶进余，胡科桥

(1.浙江理工大学浙江省现代纺织装备重点实验室，浙江杭州 310018;2.山东日发纺织机械有限公司，山东聊城 252000)

对纱线快速变化的张力进行准确测量是保证优质纺织品质量的重要环节［1－2］。接触式霍尔纱线张力传感器是一种有效的张力测量工具。在纱线保持一定张力时，霍尔式张力传感器中的悬臂梁系统受力平衡，待测张力转换为磁钢探头位移的变化，并以位移为中间参变量，建立了张力与霍尔电压之间的线性关系，从而实现纱线张力测量［3－4］。

在张力剧烈波动的情况下，磁钢探头将跟随纱线进行快速运动。随着纱线张力变化频率地增大，磁钢加速度也相应增大，从而破坏了纱线张力和由悬臂梁形变导致的应变力之间的力学平衡，对探头位置产生明显的影响，使输出张力出现明显偏差［5］，因此霍尔式张力传感器比较适合用于纱线张力变化较慢的纺织装备，例如加弹机。对于一些纱线张力变化频率较高的装备，如高速喷气织机引纬系统，霍尔式张力传感器输出结果误差较大［6］。

有学者对测力传感器在动态测量中振动误差问题展开研究。吴强等［5］通过提高测力传感器测头的固有频率，从而减小测力传感器的振动响应幅值。也有文献通过对传感器输出信号滤波的方法，从而实现动态响应修正。JAFARIPANAH 等［7－8］提出了模拟技术滤波用于误差信号的抑制，SHI等［9］发展了一种数字自适应滤波算法进行传感器响应校正。但运用滤波方法在减小振动误差信号的同时也影响了被测力有效信号的输出。滤波方法比较适合正在振荡但最终值确定的传感器信号，如称重器等［7］。但是纺织装备中，纱线张力一直处于波动变化中，少有最终值确定的情况。对于这一类问题，鲜有文献涉及。

为提高霍尔式张力传感器在纱线张力快速变化工况下的输出结果准确性，本文对霍尔式张力传感器的磁钢探头建立运动学模型，并在此基础上发展了一种用于减少由悬臂梁上磁钢自身运动惯性所造成误差的数值求解算法，提出了动态张力信号提取方法，并建立了张力测试实验台，对不同条件下的测试结果进行对比研究，验证了信号提取算法的有效性。

1 动态张力测量模型

图1为接触式张力传感器检测单元工作原理示意图。纱线压过张力传感器的测头时，忽略摩擦力，假设纱线在测头前后张力值相等。F为纱线张力对磁钢作用力，其值为

式中:T为纱线张力;α为纱线包络磁钢所形成的角度。F方向与悬臂梁所成角度为β。在悬臂梁的小变形情况下，α可以近似认为不变。

图1 基于霍尔效应的接触式纱线张力传感器工作原理Fig.1 Operation principle of Hall-type tension senor

在长度为L的纱线张力传感器悬臂梁上建立如图2所示的笛卡尔坐标系，坐标系原点设在A点上，悬臂梁自重忽略不计，B端不受力时，AB与x轴重叠。受磁钢重力G作用时，AB发生弯曲变形，B端到达B'点，AB'构成一挠曲线。B点到达B'点的距离为δ，重力G与悬臂梁构成角度φ。

图2 磁钢受重力作用下悬臂梁力分析Fig.2 Force analysis of cantilever beam undermagnet steel's gravity

在小变形的情况下，挠曲线的近似微分方程［10］

式中:E为悬臂梁材料的弹性模量;I为悬臂梁转动惯量;E与I的乘积为梁的抗弯刚度;M(x)为悬臂梁在坐标x处受到力矩的函数。

将G沿x轴与y轴方向分解。对均匀截面梁EI为常数，因受集中力G作用，故

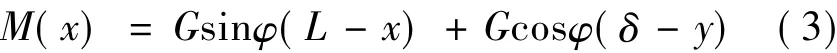
将式(3)代入式(2)，得

式(4)中δ的大小与x，y取值无关，式(4)是一个常系数非齐次线性微分方程，其特解为

考虑边界条件:当x=0时，=0且y=0;因为悬臂梁是小变形，所以当x=L时y=δ。

因此挠曲线方程为

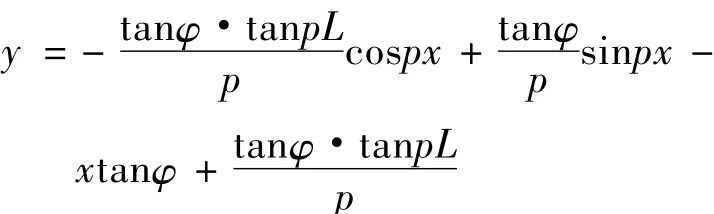
将tanpL泰勒展开

因为在张力的量程内，pL是个接近零的值，取tanpL≈

重力G在y轴方向上的分量为Gsinφ，计算振动系统的弹性系数

计算振动系统的固有频率［11］

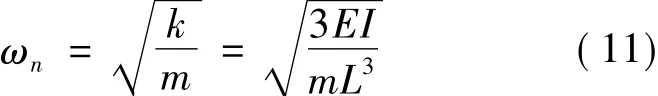
式中m为磁钢的质量。

计算振动系统受到的空气阻尼力的阻尼系数［11］

式中ζ为阻尼比。

图3示出悬臂梁受力情况。在图中，纱线张力传感器的悬臂梁在受到纱线张力的作用产生大小为s的位移。悬臂梁上的磁钢同时受到重力、纱线张力和悬臂梁因弯曲变形而产生的恢复力的作用，根据牛顿第二定律，得到动力学平衡方程

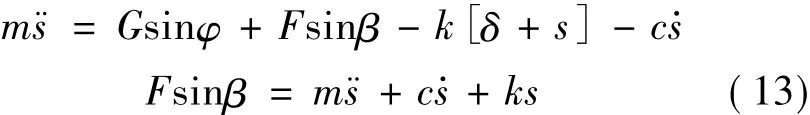
式中·s·和·s分别表示s对时间t的二阶导数与一阶导数。

将式(10)～(12)代入式(13)，得

因为挠度与霍尔电压成线性关系，得

式中:a为传感器的输出电压与悬臂梁挠度的比例系数;Ut为霍尔式张力传感器在t时刻的输出电压;U0为传感器仅受磁钢重力时的静输出电压。

将式(15)代入式(14)，得

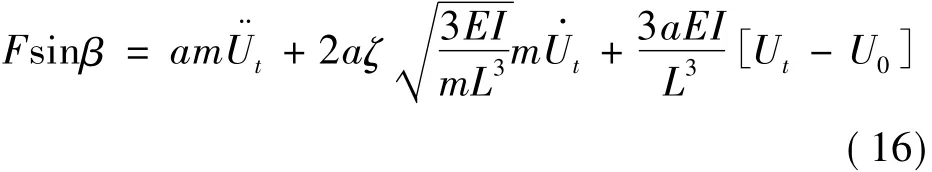
将式(16)代入式(1)，得动态张力测量模型

式(17)中 α、β、a、E、I、m、L、ζ均为张力传感器固有参数，可以通过测量方式获得。U·t，U··t分别为传感器输出电压Ut对时间t的一阶和二阶导数。

图3 悬臂梁受力分析Fig.3 Force analysis of cantilever beam

2 数值离散方法

通过A/D采样电路获得用于表示传感器输出信号的等时间间隔△t的Ut，对采集张力传感器输出的初级离散数字信号进行差分格式转化获得 ，。其中 采用二阶精度中心差分格式

式中:Ut+△t为t+△t时刻的传感器输出电压;Ut－△t为t－△t时刻的传感器输出电压。

将上述变量代入式(17)，所得T为的经动态测量模型抑制振动误差后的纱线张力输出值。

3 实验及结果分析

3.1 实验设计

为了验证上述模型及数值算法的有效性，建立了数据采集和分析实验系统。该实验系统核心部分由32位Cortex-M3微处理器和24位A/D转换模块构成，处理器按照125 kHz采样频率进行张力数据采集，并对采样结果应用误差抑制算法。实验系统如图4所示。

图4 测量系统框图Fig.4 Block diagram ofmeasurement system

在该实验系统上，分别进行了瞬态张力释放和加载2类实验，用于振动误差抑制算法有效性的验证。

图5为瞬态张力释放实验示意图。由图可知，通过悬挂重物使纱线处于张紧状态，重力不超过传感器的量程，待传感器输出稳定后，用高温火焰烧断承载纱线［5］，由于重物脱离被瞬间烧断的纱线，因此纱线张力得到迅速释放，传感器相当于获得一个阶跃输入。

图5 瞬态张力释放实验示意图Fig.5 Experiment schematic of instantaneous release of the tension

图6为瞬态张力加载实验示意图。由图可知，跨接张力传感器的纱线原先处于松弛状态，释放重物后将张力加载到纱线上。由于纱线的弹性作用，重物将产生振动现象，使纱线反复经历快速伸张收缩的过程，这个实验更真实地反映纺织装备中纱线受力情况。

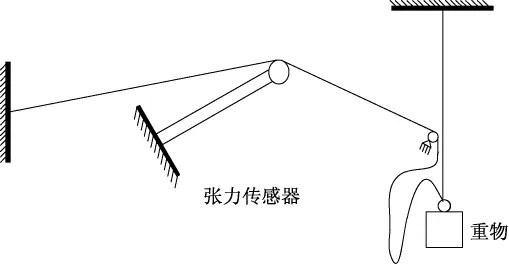
图6 瞬态张力加载实验示意图Fig.6 Experiment schematic of loading instantaneous tension

3.2 实验数据分析

图7和图8分别示出张力释放和加载2种情况下传感器输出和通过动态模型计算的输出结果。其中传感器输出曲线表示传感器输出电压依据静态测量时对应的线性关系转换得到的纱线张力与时间的关系。动态模型输出的纱线张力值由将张力传感器的输出电压代入动态测量模型式(17)得到。

图7 张力释放实验原始输出和动态测量模型输出比较Fig.7 Comparison of force between original system and dynamic measurementmodel in experiment of instantaneous release of tension

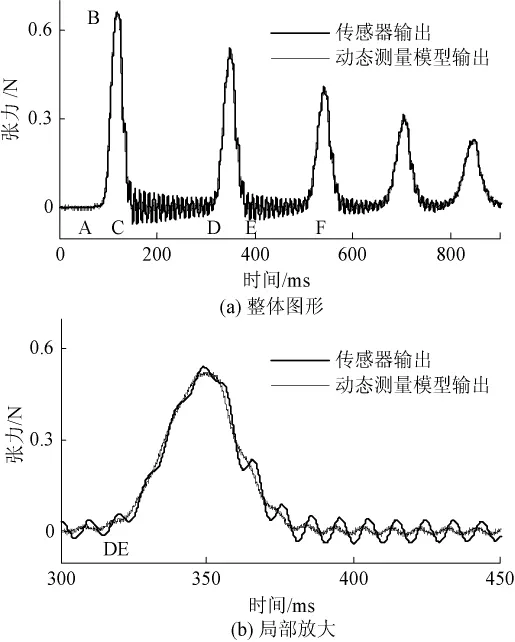
图8 张力加载实验原始输出和动态测量模型输出比较图Fig.8 Comparison of force between original system and dynamic measurementmodel in experiment of loading of tension.(a)Global view;(b)Partial enlarged view

图7中的理想输入曲线表示张力释放实验中理论纱线张力与时间的关系。对其分析如下。

1)图7中，传感器实际输出与理论输入相差很大，在纱线张力剧变时，传感器的输出值不能表示纱线真实张力值。这是因为张力传感器系统属于二阶欠阻尼机械振动系统，振荡不可避免。

2)图7中，纱线张力变化时，动态测量模型比传感器输出值更符合真实张力值。动态测量模型能有效减小因张力快速减小到零导致的振动误差。

3)图8(a)中，AB段，重物速度方向竖直向下。B点速度为零到达最低点，BC段重物受纱线张力上拉，速度方向竖直向上。在CD段及EF段重物处于空中高位，期间纱线松弛，张力为零，传感器输出表现出非张力信号的抖动特性。通过比较证实了该动态测量模型能有效去除这个抖动特性。

4)图8(b)中，局部放大了图8(a)中的DE段，可以看出在纱线张力不为零时，传感器输出也叠加着振动误差信号。DE段出现了多次极大值，与重物在DE段下落时纱线只出现1次极大值的实际情况不符。而经动态测量模型振动误差抑制算法处理后的张力，也只出现了符合实际情况的1次极大值。在纱线张力不为零的情况下，动态测量模型也能有效地减小因张力快速变化导致的振动效应产生误差。

5)从图7、8中可看出动态测量模型先于传感器输出做出变化，说明在纱线张力剧变时悬臂梁对张力信号的响应存在延时。动态测量模型能更迅速地响应张力的激励。

6)图7的0～20 ms时间段中，在A点前，传感器输出与动态测量模型输出曲线几乎重合，动态测量模型同样适用于稳定张力的测量。

4 结论

理论分析和实验证明，接触式张力传感器的检测单元动态测量模型及其数值求解算法能够抑制检测信号中因快速张力变化引起的振动效应所产生的误差。同时动态测量模型也可以用于稳定张力的测量，能更迅速地响应张力的激励。通过动力学分析建模可知，模型能从根本上减小误差。本文研究为动态条件下的接触式张力传感器运用提供了理论参考。

［1］ ADANUR Sabit，QI Jing.Property analysis of denim fabrics made on air-jet weaving machine:partⅡ，effects of tension on fabric properties［J］.Textile Research Journal，2008，78(1):10 －20.

［2］ 庾在海，吴文英，陈瑞琪.纱线张力动态测试方法［J］.自动化仪表，2005，26(10):33－35.YU Zaihai， WU Wenying， CHEN Ruiqi.Dynamic testingmethod for yarn tension［J］.Process Automation Instrumentation，2005，26(10):33－35.

［3］ 陈宁，宋传明，陈文芗.霍尔式力传感器的研制［J］.厦门大学学报:自然科学版，2005，44(1):47－49.CHEN Ning， SONG Chuanming， CHEN Wenxiang.Design of the Hall's force sensor［J］.Journal of Xiamen University:Natural Science Edition，2005，44(1):47－49.

［4］ 邱召运.微张力测量模型设计与实验研究［J］.传感技术学报，2009，22(4):608－612.QIU Zhaoyun.Design and experimental study of microtension measurement models［J］.Chinese Journal of Sensors and Actuators，2009，22(4):608 －612.

［5］ 吴强，吉爱红，王周义，等.一种测力传感器固有频率的提高与测试［J］.传感技术学报，2010，23(2):235－238.WU Qiang， JI Aihong， WANG Zhouyi， et al.Improvement and test for a force sensor s natural frequency ［J］.Chinese Journal of Sensors and Actuators，2010，23(2):235－238.

［6］ 祝章深.纬纱飞行和主喷射工艺参数［J］.中国纺织大学学报:自然科学版，1998，24(5):84－87.ZHU Zhangchen.Pneumatic weft insertion and main jet parameters［J］.Journal of Donghua University，Natural Science Edition，1998，24(5):84－87.

［7］ JAFARIPANAH M，AL-HASHIMIBM，WHITE N M.Application of analog adaptive filters for dynamic sensor compensation［J］.IEEE Transactions on Instrumentation and Measurement，2005，54(1):245 －251.

［8］ JAFARIPANAH M，ALHASHIMIB M，WHITE N M.Dynamic sensor compensation using analogue adaptive filter compatible with digital technology ［J］.IEE Proceedings—Circuits， Devices and Systems，2005，152(6):745－751.

［9］ SHIW J，WHITE N M，BRIGNELL J E.Adaptive filters in load cell response correction［J］.Sensors and Actuators A，1993，37－38:280－285.

［10］ AKSHOY Ranjan Paul，PIJUSH Roy，SANCHAYAN Mukherjee.Mechanical Sciences: Engineering Mechanics and Strength of Materials［M］.India:Prentice-Hall of India，2006:492.

［11］ 陈帮，郭明金，王熙熙.光纤光栅振动传感器的振动理论分析［J］.武汉理工大学学报:信息与管理工程版，2012，34(2):143－146.CHEN Bang，GUO Mingjin，WANG Xixi.Vibration theory analysis on fiber bragg grating vibration sensor［J］.Journal of Wuhan University of Technology:Information ＆ Management Engineering Edition，2012，34(2):143－146.