经编电子送经的模糊PID控制设计
2013-12-19夏风林蒋高明
刘 苏,夏风林,张 琦,蒋高明
(江南大学针织技术工程研究中心,江苏无锡 214122)
经编电子送经系统是通过控制伺服电动机驱动经轴按照工艺要求连续精确稳定地送出纱线来满足编织需要的系统,自从德国Karl Mayer于1981年首次在经编机上配置EBC电子送经系统后[1],电子送经系统以其送经精确、送经量可切换和调整方便等特点,适应了经编产品高品质及花色性要求。
目前国内外学者对经编电子送经系统的控制方式研究较多[2-3],部分学者还研究了送经 PID控制设计,即通过PID调节使经轴电动机指令转速与实际转速之间的差值趋于零,达到精确控制经轴电动机转速的目的[4-5]。在经编送经过程中,普通 PID的比例、积分和微分3个参数无法根据经轴电动机速度的变化实时调整[6],尤其是在开停车和多速送经序列切换时,经轴电动机指令速度与实际速度差值波动很大,影响高速经编机送经控制的实时性和动态稳定性。本文通过引入模糊控制技术,结合普通PID控制算法,为经编机电子送经系统设计了模糊PID控制算法,通过模糊PID实时调整经轴电动机的速度,可减小实际生产过程中出现的送经误差,改善送经系统的控制精度和跟随响应特性,有利于提高经编机的运转性能。
1 经编电子送经系统控制原理
1.1 模糊PID控制的提出
在经编生产中,经轴外周长、主轴转速等送经工艺参数经常变化,难以建立出精确的数学模型,传统的普通PID控制算法虽然成熟、稳定性好,但由于普通PID的参数不易实时在线调整,在应用中影响送经系统的控制品质,表现为抗扰动性和适应性较差[7],导致经编机正常运行时出现断纱、松纱等问题,难以适应实际生产中非线性、不确定的送经控制要求。模糊PID控制算法对这种复杂的系统处理能力强,控制性能好,根据专家实际控制经验制定控制规则,不依靠精确的模型,算法比较灵活[8],可以有效地降低编织过程中因送经系统内部或经轴参数差异等外部干扰带来的送经误差,减少断纱、解决纱线张力波动过大、横条明显等问题,因而这种方式特别适用于经编用电子送经系统。
1.2 系统工作原理
整经工艺合理时,通过简洁的半闭环控制式送经系统也能保证良好的送经精度[9]。图1为经编机半闭环电子送经系统的工作原理图。经编机运行时运动控制卡接收主轴位置信号和上位机的送经工艺参数,根据设定的送经量、经轴初始外周长和主轴转速等数据计算出当前的经轴电动机指令速度,向送经驱动器发出送经指令,控制经轴电动机按指令速度运转,并通过其内置的编码器将经轴电动机实际转速反馈给伺服驱动器和运动控制卡,运动控制卡将电机的指令速度和反馈速度比较,通过比较确定速度差值,由模糊PID调整电动机速度,使指令转速与实际转速之间的差值趋于零。
2 电子送经系统控制算法
2.1 控制算法基础
1)纱线均匀逐层缠绕在经轴上,经轴即时纱绕外周长与经轴退绕圈数呈线性关系[10]。
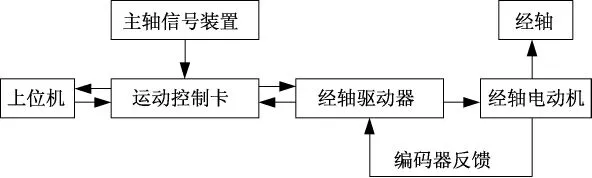
图1 半闭环电子送经系统工作原理图Fig.1 Working principle of semi-closed loop electronic yarn let-off system
2)主轴1转,编织机构需要消耗的纱线长度与经轴送出纱线长度相等。
2.2 控制算法
2.2.1 经轴电动机目标转速
在编织过程中,经轴退绕总圈数由经轴电动机上的编码器获得,根据运动控制卡读取的初始值,经轴即时外周长Ci的计算式如下:
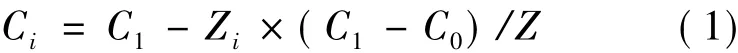
式中:Ci为经轴的即时外周长,mm;C1为经轴的满卷周长,mm;C0为经轴的空轴周长,mm;Z为经轴满卷时的绕纱圈数;Zi为经轴满卷至现时的退绕总圈数。
运动控制卡读取当前送经量FZi和经轴即时外周长Ci,由一定的主轴速度下需要消耗的纱线长度与经轴送出纱线长度相等,可得经轴电动机目标转速[11]
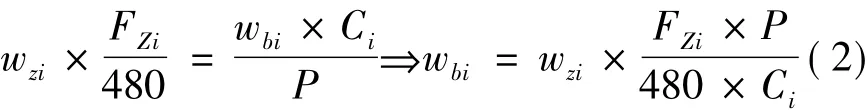
式中:i为周期标号;wzi为主轴转速,r/min;wbi为第i周期时经轴电动机的设定转速值,r/min;FZi为设定的当前送经量,mm/Rack,P为经轴驱动电动机与经轴间的机械减速比。
2.2.2 经轴电动机编码器反馈速度
主轴转速可通过测量主轴编码器输出得到,运动控制卡根据主轴编码器采样周期t(ms)、该采样周期内主轴编码器发出的脉冲数Xi和主轴编码器每转脉冲数K,即可获得当前主轴转速
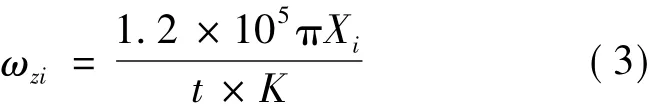
则得经轴电动机转速为
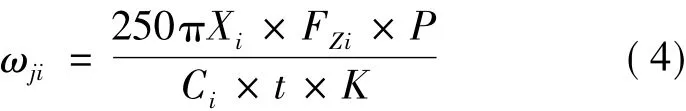
2.2.3 运动控制卡比较差值
运动控制卡比较经轴电动机编码器反馈的实际电动机速度与经轴电动机的指令速度,得到差值

确定速度差值后,再由运动控制卡把速度差值转化为速度调节值,从而得到新的经轴电动机速度指令值输出给送经驱动器,由经轴电动机驱动经轴按工艺要求的送经量送纱。
3 送经模糊PID控制设计
3.1 普通PID控制结构
在送经系统中,普通PID控制是根据运动控制卡的经轴电动机指令速度值和经轴电动机编码器反馈的实际值之间的偏差E来实现的,如图2为送经的普通PID控制原理图。通过将经轴电动机偏差的比例(P)、积分(I)、微分(D)组成控制量,以此对送经系统的偏差进行调节。比例环节的作用是对偏差作出反应,一旦产生偏差,便立即进行补偿,以减少偏差;积分环节的作用是消除静态误差;微分环节的作用是阻止偏差的变化,减小超调量。
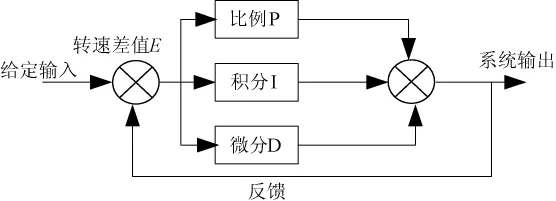
图2 普通PID控制原理图Fig.2 Working principle of common PID control
3.2 模糊PID控制结构
电子送经控制系统的要求是完成经纱送经量的精确控制,即实时控制经轴电动机的转速。开停车和多速送经序列切换时,送经系统中经轴转速变化很大,为避免普通PID控制的3个参数无法根据经轴转速变化在线整定,而导致送经量不精确、张力波动过大、横条明显等不足;将模糊控制技术引入到普通PID控制中,推导出一种模糊PID控制算法,在送经系统的模糊PID实时运行前,需将送经模糊规则及有关送经参数作为信息元存入运动控制卡信息库中;模糊PID控制器的输入是经轴电动机转速变化和变化率,利用送经模糊规则进行推理,查询运动控制卡内模糊规则表对送经PID参数进行调整,得出合适的PID参数,实现转速的精确控制。模糊PID系统结构图如图3所示。
系统对送经PID的比例、积分和微分3个参数进行修正调整,机制为
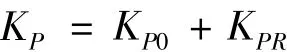
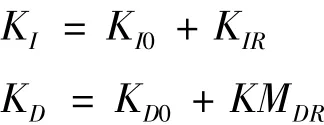
式中:其中KP0、KI0、KD0为送经系统 PID参数初始值;KPR、KIR、KDR为参数在线修正值;KP、KI、KD为最终送经系统调节参数输出值。
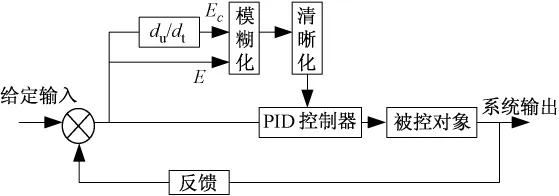
图3 模糊PID控制结构Fig.3 Structure of fuzzy PID control
3.3 模糊PID控制参数值域定义
在电子送经系统中,经轴电动机指令转速与实际转速的差值E及其变化率EC的实际变化范围,称为误差及其变化率的基本论域。模糊控制器论域常用[-6,6][12],这样论域的离散值有 13 个,理论上离散值个数越多,控制精度越高,但离散值个数多会导致系统运算量增大,反而引起系统响应滞后甚至崩溃。根据送经系统控制的需要,选择7个离散值即设置论域为[-3,3],正常生产状态下经轴电动机转速差值E一般较小,当送经量切换时差值可能很大,根据常见的状况设置其基本论域为[-500,500],变化率EC的取值范围[-5 000,5 000],由送经系统调试经验知,PID控制器3个参数修正值KPR、KIR、KDR的取值范围一般是[-3,3]、[-0.1,0.1]、[-0.01,0.01],再对模糊控制各参数值进行论域变换,使之落入设置论域里,基本论域里各参数E、EC、KPR、KIR、KDR变换到设置论域里分别是e、ec、kp、ki、kd,同时可得各参数的量化因子,如E的量化因子为0.006,然后对已经论域变换的参数值进行模糊化处理,输入e、ec和输出kp、ki、kd都均匀量化为7 级,它们的模糊子集定义为{NB,NM,NS,ZO,PS,PM,PB},分别对应负大、负中、负小、0、正小、正中、正大7个语言变量。模糊控制中,对论域U中的任一元素x,都有一个数A(x)∈[0,1]与之对应,则称A为U上的模糊集,A(x)称为x对A的隶属度,当x在U中变动时,A(x)就是一个函数,称为A的隶属函数,隶属度A(x)越接近于1,表示x属于A的程度越高,A(x)越接近于0,表示x属于A的程度越低,用取值于区间0~1的隶属函数A(x)表征x属于A的程度高低。本文设计中各参数都选择左边z形、中间三角形、右边s形的隶属函数,各参数的隶属度曲线如图4所示。
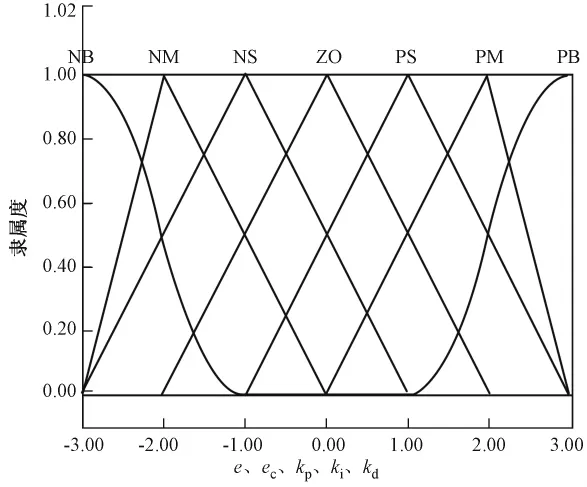
图4 各参数隶属度曲线Fig.4 Membership grade curve of every parameters
3.4 模糊控制规则表的确立
根据送经系统中PID参数KP、KI、KD对实际输出的影响情况,可得出系统在运行过程中针对不同的经轴电动机差值,KP、KI、KD3个参数的调整原则[13]:
1)在开停车时,经编机主轴转速变化率大,使得经轴电动机转速变化率偏大,送经量的误差增大,此时增加比例放大系数KP,以迅速响应送经误差,当经轴电动机出现振动发出噪音时,再将KP调小10%并观察布面,若布面横条疵严重,说明系统出现超调,可去掉积分作用,令KI=0,减小经轴电动机指令转速与实际转速的偏差。
2)送经系统在不同送经量的横列间切换时,送经量出现跃变、经轴电动机指令转速与实际转速的偏差较大,而偏差变化率不大,可将KP调大至经轴电动机出现振荡,然后再减小10%,以保证经轴电动机具有一定的响应速度;再逐步减小KD值,以降低因系统超调振荡而引起的送经量波动;同时选取适当的KI值提高送经系统的准确度。
3)送经系统正常运行时,送经量偏差较小,适当减小KP和KI的值可使送经系统具有较稳定的送经指令值,同时为避免输出送经实际值在送经量给定值附近振荡,以及考虑送经系统的抗干扰能力,应选取适当的KD值。
根据选择的隶属函数以及上述送经系统的控制经验,可得送经系统模糊控制规则,如表1~表3所示[14]。
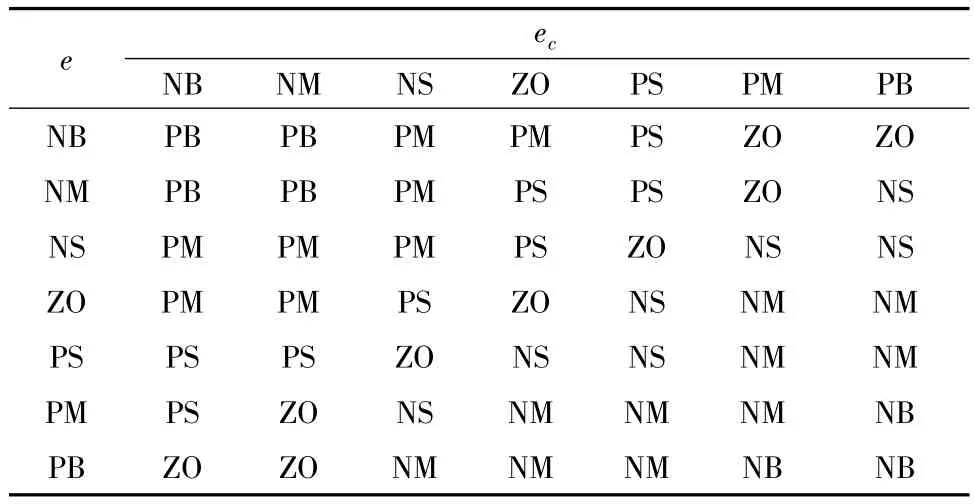
表1 模糊KP的规则表Tab.1 Fuzzy rule tab le of KP
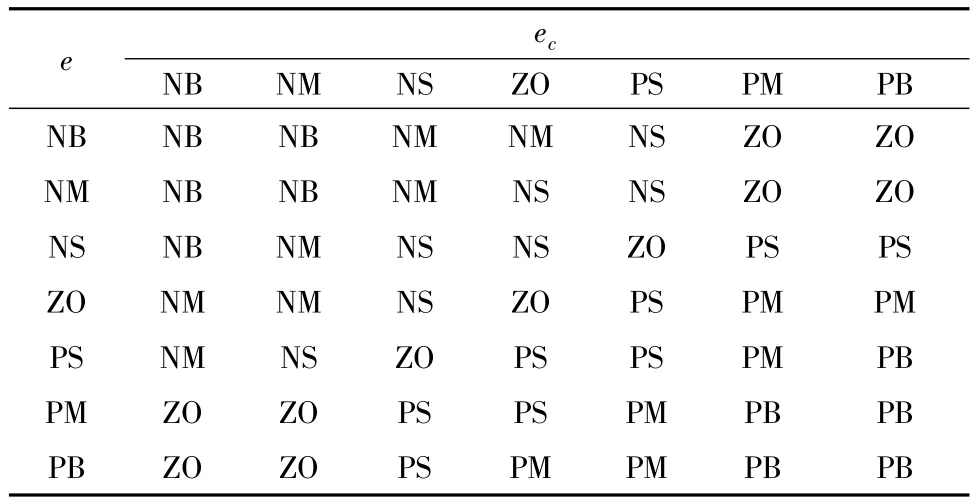
表2 模糊KI的规则表Tab.2 Fuzzy rule table of KI
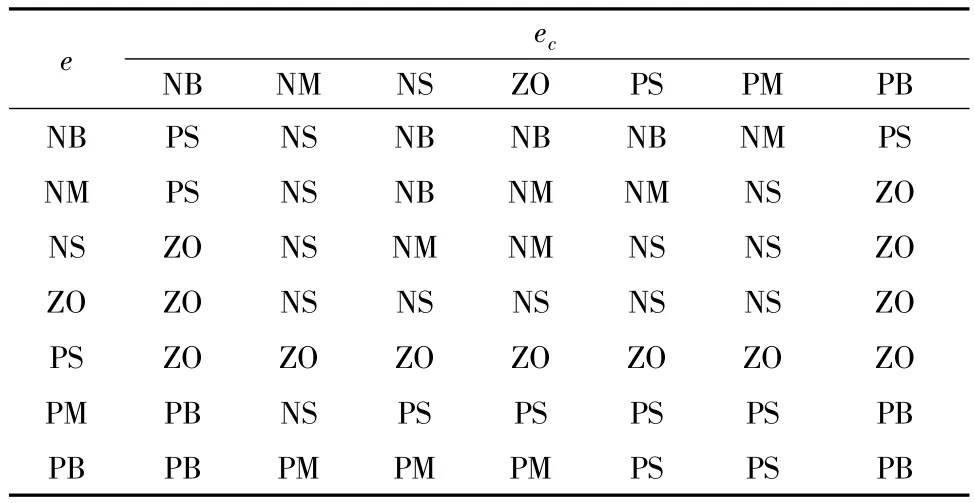
表3 模糊KD的规则表Tab.3 Fuzzy rule table of KD
4 模糊PID控制系统仿真分析
为了验证模糊PID规则表的合理性与有效性,采用MatLab对送经量控制进行仿真测试。编制MatLab程序时,首先选定仿真模型,确定送经PID初始值;接着定义输入变量(E、Ec)和输出变量(KP、KI、KD及其隶属函数);然后定义送经系统模糊规则列表矩阵;最后进行仿真计算,并输出仿真图像[15]。根据这个思路,分别编制普通PID和模糊PID的MatLab程序并设置相同的初始工艺参数进行测试,得到普通PID和模糊PID控制下的系统响应曲线,见图5。分析图可得:
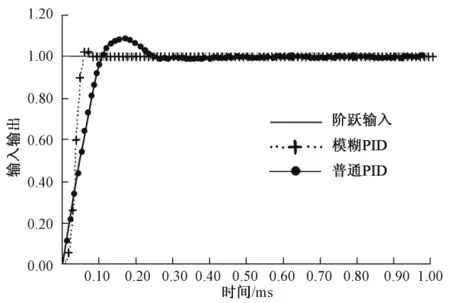
图5 2种PID控制响应曲线对比Fig.5 Two response curve comparison of PID control
1)上升时间:模糊 PID调节上升时间为0.08 ms,普通PID调节上升时间为0.2 ms。上升时间短,表现为系统响应快,在经编机正常编织过程中,能有效减轻运转横条。
2)调节时间:模糊PID控制调节时间0.1 ms远小于普通PID调节时间0.28 ms,这特别适合于高速生产的多速送经序列切换,控制系统调节越快,不同送经量切换时间越短,送经张力波动越小。
3)超调量:模糊PID超调量0.34%和普通PID超调量7.3%相比,超调量减小,则送经系统动态稳定性高,送经系统运行时能保证送经量精准,张力波动较小。
5 结论
1)经编送经系统中控制对象变化复杂,采用普通PID控制效果并不够理想。通过建立适当的模糊规则,设计出采用模糊PID控制的经编送经控制系统,对比例、积分和微分3个PID参数进行实时在线调整。
2)送经模糊PID控制参数值域定义可选择为7个离散值,即输入变量和输出变量均可均匀量化为7级,并根据调试经验可得到模糊控制规则。
3)MatLab仿真表明,模糊PID较普通PID控制,调节时间短,超调量小,有效提高了经编送经系统的响应性能,对改善停车横条疵,减小张力波动和提高产品质量有很大的帮助。algorithm on warp knitting multi-speed electronic let-off system[J].Journal of Textile Research,2007,28(9):110-113.
[1] KARL Mayer.EBA warp feed system.Kettenwirkpraxis[J].2000(2):25 - 26.
[2] 王文进,蒋高明.经编多速电子送经系统控制过程与控制算法[J].纺织学报,2007,28(9):110-113.WANG wenjin,JIANG Gaoming.Control process and
[3] 孔震,蒋高明,夏风林.经编机伺服控制系统的参数调节方法[J].纺织学报,2008,29(10):102-108.KONG Zhen,JIANG Gaoming,XIA Fenglin.Parameters adjusting methods of warp knitting servo-control system[J].Journal of Textile Research,2008,29(10):102-108.
[4] 田宁波,袁嫣红,张建义.高速经编机电子送经控制系统的设计[J].机电工程,2011,28(2):187 -190.TIAN Ningbo,YUAN Yanhong,ZHANG Jianyi.Design of electronic let-off control system of high speed warp knittingmachine[J].Journal of Mechanical& Electrical Engineering,2011,28(2):187 -190.
[5] 杨薇,史伟民,张立朝.基于PLC的高速经编机电子送经控制系统[J].机电工程,2009,26(9):87-89.YANG Wei,SHIWeimin,ZHANG Lichao.Electronic let-off control system based on PLC of high-speed warp knitting machine[J]. Mechanical & Electrical Engineering Magazine,2009,26(9):87 -89.
[6] 郭亚军,马大为,王晓锋.反演单神经元PID复合控制在伺服系统中的应用[J].南京理工大学学报,2011,35(5):693 -696.GUO Yajun,MA Dawei,WANG Xiaofeng.Application of backstepping single neuron PID compound control to servo system[J].Journal of Nanjing University of Science and Technology,2011,35(5):693 -696.
[7] 文乐,高林,戴义平.透平压缩机组的模糊PID控制与特性研究[J].西安交通大学学报,2011,45(7):76-81.WEN Le,GAO Lin,DAI Yiping.Study on fuzzy PID control of turbine-driven centrifugal compressor[J].Journal of Xian Jiaotong University,2011,45(7):76 -81.
[8] 汤红诚,李著信.Matlab在模糊PID伺服系统控制中的应用[J].仪器仪表学报,2003,24(z2):595 -596.TANG Hongcheng,LI Zhuxin.The use of MatLab in fuzzy PID servo system control[J].Chinese Journal of Scientific Instrument,2003,24(z2):595 -596.
[9] 夏风林.伺服控制电子送经测速压辊的作用分析[J].纺织学报,2008,29(7):95-99.XIA Fenglin.Function analysis of feedback roller on electrical beam control based on servo control[J].Journal of Textile Research,2008,29(7):95 -99.
[10] 王道兴.电子送经系统经轴线速度计算公式的探讨[J].纺织学报,2007,28(12):110 -112.WANG Daoxing.A probe to the calculation model of the warp beem linear speed of electronic let-off system[J].Journal of Textile Research,2007,28(12):110 -112.
[11] 张琦,汤友章.经编机电子送经反馈控制及误差分析[J].针织工业,2008(8):34 -36.ZHANG Qi,TANG Youzhang.Knitting machine,electronic let-off by the feedback control and error analysis[J].Knitting Industries,2008(8):34 - 36.
[12] 许力.智能控制与智能系统[M].北京:机械工业出版社,2007:106.XU Li.Intelligent Control and Intelligent Systems[M].BeiJing:China Machine Press,2007:106.
[13] 周黎英,赵国树.模糊PID控制算法在恒速升温系统中的应用[J].仪器仪表学报,2008,29(2):405-409.ZHOU Liying,ZHAO Guoshu.Application of fuzzy-PID control algorithm in uniform velocity temperature control system of resistance furnace[J].Chinese Journal of Scientific Instrument,2008,29(2):405 -409.
[14] 田凡.电液伺服系统模糊 PID控制仿真与试验研究[D].太原:太原理工大学,2010.TIAN Fan.Fuzzy PID control simulation and test study on electro-hydraulic servo system[D].Taiyuan:Taiyuan University of Technology,2010.
[15] 高宏伟,赵宝永,付兴武.模糊自整定 PID控制策略的Matlab仿真研究[J].电气传动自动化,2002,24(5):21-23.GAO Hongwei,ZHAO Baoyong,FU Xingwu.MatLab simulation research on fuzzy self-adjusting PID control strategy[J].Electricdrive Automation,2002,24(5):21-23.
