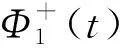带第一类间断点的RH问题
2013-12-18田进凤
杨 娟 田进凤
(1.宁夏大学 数学计算机学院,宁夏 银川750021; 2.宁夏大学 民族预科教育学院,宁夏 银川750002)
1962年,路见可教授[1-2]首次提出并解决了复合边值问题,简称RH问题.近年来,有不少学者研究复合边值问题,2000年程平旺[3]研究了双解析函数的复合边值问题;2001年郑神州和渠刚荣[4]研究了解析函数类中的复合型边值问题;2002年张霞、李星[5]研究了非正则型复合边值问题;2005年路见可[6]研究了带平方根的Hilbert边值问题;陈振华,2009年郭定辉[7]讨论并求解了带平方根的复合RH边值问题的两种情况.本文在上述工作的基础上,将复合边值问题进行推广,讨论了带第一类间断点的正则型复合RH边值问题在封闭曲线上的一般解.我们先用消去法将所提出的RH问题化为一个H问题,再进一步化为间断系数的R问题,然后根据指标的不同描述其解,并以定理的形式给出结果.
1 问题的提出
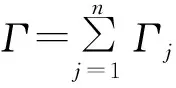
复合RH问题提法如下:求在D内全纯,且连续到L与Γ两侧(端点可能除外)上的函数Φ(z),使其满足下列条件
1)Φ+(τ)=G(τ)Φ-(τ)+g(τ),τ∈Τ,其中G(τ),g(τ)∈H于Γ,又G(τ)≠0;
(1)
(G(τ),g(τ)满足Holder条件(记为H)且G(τ),g(τ)都是L上的已知函数).
2)Re{[a(t)+ib(t)]Φ(t)}=c(t),t∈L,
(2)
其中a(t),b(t),c(t)为∈H于L的实函数,(a(t),b(t),c(t)均为已知在L上属于H的实函数,且a2+b2≠0)还设它们在L上有若干个第一类间断点c1,…,cn,并限于考虑正则型情况:a(t)±ib(t)≠0于L上.
要注意的是,在Γ的各端点aj,bj附近,Φ(z)可允许有不到一阶的奇异性.可按1)的要求把各端点也分为普通端点和特异端点两类,也称为上述RH问题的普通端点和特异端点.求解时,要求Φ(z)属于某一解类,例如h(c1,…,cq),其中c1,…,cq为某些普通端点,即要求Φ(z)在这些端点附近有界,而在其它普通端点可以有不到一阶的奇异性,而在所有特异端点附近只能至多是几乎有界的.
在各Γj上取定logG(τ)的一个连续分支,例如,记
使得0 Κ称为所提RH问题的指标. Χ+(τ)=G(τ)Χ-(τ),τ∈Γ (3) 于是在h(c1,…,cq)类中,求出D中相应R问题1)的一个特解 利用消去法,令 Φ(z)=Φ1(z)+Χ(z)Φ0(z). (4) 其中Φ0(z)为D中新的未知函数.当τ∈Γ时,因Φ1(z)满足(1),故由式(3)知 下面证明Φ0(z)在各端点处也是解析的. 由Χ(z)在端点c(=aj或bj)附近的性质知,Χ(z)=(z-c)γcχc(z),其中Reγc=ac,-1 Χ(z)Φ0(z)∈h(c1,…,cq). 如c为一特异端点,则a0=0,因此Χ(z)在c附近有界,且不等于0.今Φ(z)既以c为孤立奇点,又只有不到一阶的奇异性,故必以c为常点.注意到Φ1(z)在z=c附近几乎有界,可见,如果RH问题有解,则解Φ(z)也必在z=c附近几乎有界,如c∈(c1,…,cq),则因0 总之,无论c是Γ上的哪一种端点,Φ0(z)总以它为常点,因而Φ0(z)在D内全纯.又因Φ1(z),Χ(z)都连续到L上,且Χ(z)≠0,故Φ0(z)也必连续到L上. 反之,如Φ0(z)在D内全纯,且连续到边界L上,则也容易证明由式(4)所确定的分区全纯函数Φ0(z)必满足式(1),且连续到L上.这样,提出的RH问题就转化为求在D内全纯,且连续到边界L上的函数Φ0(z),使它满足由式(2)转化的相应条件.将式(4)代人式(2),可得下述条件: Re{[a(t)+ib(t)]Χ(t)Φ0+(t)}=c*(t),t∈L (5) 其中 c*(t)=c(t)-Re{[a(t)+ib(t)]Φ1(t)}. 这样,原RH问题就转化成了L上带间断系数的H问题(5). 不失一般性,以下不妨设L为单位圆周|t=1|,则式(5)可改写为 (6) 因此式(6)又可改写为 (7) 则问题(5)可化为下列带有间断系数的R0问题(即要求Φ0(∞)有界) Ω+(t)=G(t)Ω-(t)+g(t),t∈L (8) 问题(8)的解也可分成一些解类,也是Ω(z)所属的解类,例如,要求式(8)的解属于h(c1,…,cq),当然c1,…,cq都是普通结点.于是就可求出式(8)亦即式(5)在该类中的指标为 故这个H问题的指标为:Κ=κ+2χ. 下面先考虑齐次问题(c*=0),则由文献[8]可知问题(8)的典则函数为 X1(z)=z-kX*(z), 当Κ≥0时,这时齐次问题(8)(其中g(t)≡0)在R0中的一般解为 Ω(z)=Χ1(z)(C0zΚ+C1zΚ-1+…+CΚ), Φ(z)=Χ1(z)(C0zΚ+C1zΚ-1+…+CΚ),z∈S+ (9) (10) (11) 定理1 齐次H问题(5)(c*≡0):当Κ≥0时,有一般解为式(9),其中Ck要满足条件(10),这个一般解中含有Κ+1个任意实常数:当Κ<0时,它只有零解. 对非齐次H问题(5)来说,只须求出其一个特解,再加上相应齐次问题的一般解就是它的一般解.对(7)式两边取共轭,得 (12) 当Κ≥0时,这时问题(8)在R0中有一个特解 (13) 则 (14) 再加上相应齐次问题的一般解,(9)式就是所求一般解. 当Κ<0时,这时非齐次R问题(8)在R0中的可解条件为 这就是 (15) 定理2 非齐次H问题(5),当Κ≥0时,有一般解 Φ(z)=Φ0(z)+Χ(z)(C0zχ+C1zχ-1+…+Cχ), 其中Φ0(z)以式(13)给出,而C0,…,CΚ须满足条件(11);当Κ<0时,当且仅当条件(15)满足时,问题有唯一解(13).此问题的一般解有Κ+1个自由度. 根据上面的结论,对原RH问题作出以下的讨论. 1)设g≡0,c≠0,根据定理1,当Κ≥0时,相应H问题(8)的一般解可写成 Φ0(z)=c1Ψ1(z)+…+c2Κ+1Ψ2Κ+1(z). (16) 当Κ<0时,由于相应H问题只有零解,从而原RH问题也只有零解. 2)设g≡0,c≠0,由于这时可取Φ1(z)=0,故Φ(z)=Χ(z)Φ0(z),而Φ0(z)为D中非齐次H问题(7)的解,由定理2,当K≥0时,相应H问题有一般解 其中Φ0(z)为特解,则原RH问题有一般解 (17) 其中cj仍为实任意常数.当Κ<0时,当且仅当c*(t)从而c(t)满足-2Κ-1个实条件时,相应H问题从而原RH问题才有解,且有唯一解. 3)设g≠0,于是Φ1(z)≠0.这时又可分为两种情况: 通过以上讨论可以得到如下定理 定理3 当Κ>0时,有:1)对原RH问题,其一般解中含有2Κ+1个任意实常数;2)对齐次问题(c=0,g=0)只有零解;3)对准齐次问题有唯一非零解;4)对真非齐次问题,当且仅当问题中各已知函数间满足-2Κ-1个实条件时,才有唯一解. 参考文献: [1] Lu Jianke.On compound boundary problems[J].中国科学(A辑),1965,14(11):45-47. [2] 路见可.复合边值问题[J],武汉大学学报(自然科学版),1962,8(1):25. [3] 郑神州,渠刚荣.N-解析函数类中的复合型边值问题[J].北方交通大学学报,2001,25(3):37-40. [4] 张霞,李星.非正则型复合边值问题[J].宁夏大学学报(自然科学版),2002,23(3):193-197. [5] 路见可.On Hilbert Boundary Value Problems With Radical [J].Acta Mathematica Scientia,2005(4):755-760. [6] 孙凤琪.一类具有间断系数的RH边值问题求解[J].吉林大学学报(理学版),2007,45(3):389-392. [7] 陈振华,郭定辉.带平方根的复合RH边值问题两种情况的讨论与求解[J].湘潭大学学报(自然科学版),2009,31(1):27-33. [8] 路见可.解析函数边值问题[M].武汉:武汉大学出版社,1984:99-104.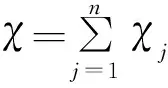
2 化成H问题
3 化为R问题
4 对H问题求解
4.1 齐次问题(c*(t)≡0)


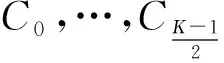
4.2 非齐次问题(c*≠0)


5 RH问题的求解