基于SAS程序模拟运算的函数模型Y=(a+bX)/X+ε参数估计及其应用

贾洪艳

(连云港职业技术学院 信息工程学院， 江苏 连云港222006)

由一个或者一组非随机变量来估计或预测某一个随机变量的观测值时，所建立的数学模型和进行的统计分析称为回归分析[1].长期以来，回归分析在宏观经济预测、医疗诊断、农业产量分析等方面得到了广泛应用.回归分析本质上是借助于函数模型，分析并确定函数模型中的参数.一直以来，由于计算手段的限制，对模型参数的估计常常依赖单因素方差分析、最小二乘法等经典统计方法，这些经典统计方法都有一个共同的特点，那就是参数估计必须有明确的数学公式.近十几年来，计算机技术的飞速发展，以及吉布斯抽样方法(Gibbs方法)的引入，为回归分析拓宽思路和方法提供了可能.本文依据函数模型Y=(a+bX)/X+ε，根据贝叶斯统计原理，对模型进行参数估计，然后利用SAS程序对参数进行概率抽取，从而实现对模型的参数估计.

1 函数模型的经典统计学估计

本文针对如下函数模型讨论

(1)

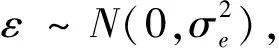
1.1 最小二乘估计法

由回归模型(1)，设

(2)

或者

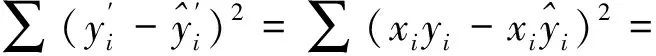
1.2 极大似然估计法

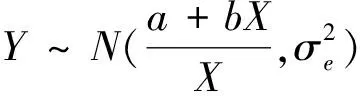
由于n组样本观测值可看作n个相互独立的随机变量，因此其似然函数为

利用

可计算出参数a,b的估计值，其估计结果表达式为

依据上述参数a,b的估计公式，对参数进行估计.

2 贝叶斯估计法

2.1 贝叶斯统计原理

设θ为包含所有未知参数的向量，p(θ|Y)是θ关于事件Y的条件概率，由统计学原理[2]知

p(θ,Y)=p(Y)p(θ|Y)=p(θ)p(Y|θ)

进一步有

(3)

其中:p(θ)和p(θ|Y)分别为先验概率和后验概率,p(Y|θ)为Y的概率密度函数.由于p(Y)无法计算且不依赖参数θ，故可略去，(3)式可进一步改写为

p(θ|Y)∝p(θ)p(Y|θ)

(4)

依据(4)式可以推导出θ中各个参数的后验分布.由于这些后验分布并不是明确的数学公式，因此，需要编写SAS程序，依据SAS程序，运用Gibbs抽样产生后验样本，通过一定的方法，分析该后验样本数据，进而获得该参数的估计.

2.2 函数模型参数的后验分布

(5)

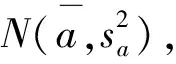
(6)

(7)

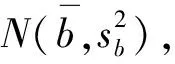
(8)

(9)

(10)

3 基于SAS程序的函数模型参数的Gibbs模拟算法

2)根据式(6)～式(7)，运用SAS程序更新a;

3)根据式(8)～式(9)，运用SAS程序更新b；

5)重复步骤2)～步骤4)t轮；

6)分析样本(a(1),b(1),σ2(1)),(a(2),b(2),σ2(2)),…，(a(t),b(t),σ2(t)),计算各参数的估计值.

4 实例分析

选用文献[5]中例12.1演示上述算法.

例研究“岱字棉”自播种至齐苗(以80%出苗为准)的天数(X)与日平均土温(Y，℃)的关系，得表1结果，试作回归分析.

表1 土温(Y,℃)和岱字棉播种至齐苗天数(X)的关系

5 结束语

长期以来，对数学模型参数进行估计，一直采用最小二乘法、极大似然法等经典统计方法.这些方法的主要优点是利用偏导函数指导搜索寻优方向，搜索效率比较高，在适合的初始值条件下，可以较快实现目标函数的优化.但是，这些方法也明显存在着诸多缺陷，主要体现在：(1)对于一个需要进行参数估计的非线性方程必须提供其偏导函数，但事实上某些方程本身较为复杂，不易获得其偏导函数.(2)编制通用软件难度较大.(3)对于不同数据进行估计时，必须根据数据的基本情况对模型提供合适的初始值，否则很容易陷入局部最优陷阱.尽管贝叶斯方法早就被提出，但是，由于计算上的困难，其统计方法很少提及.得益于计算机技术的快速发展，贝叶斯方法重新被提起.贝叶斯统计对所要进行参数估计的非线性方程，不需要提供其偏导函数，只是对方程模型的参数进行概率抽取，因此，无论方程复杂与否，均不受影响.同时，与经典统计不同的是，贝叶斯学派很重视先验信息的收集、挖掘和加工，使它数量化，形成先验分布，参加到统计推断中来，从而极大地提高了统计推断的质量.本研究尝试将SAS程序和贝叶斯统计相结合对数学模型参数进行估计，为统计方法提供了新的手段和途径.

[1]何蕴理，贺亚平，陈中和，等.概率论与数理统计[M].北京：高等教育出版社，2010.

[2]茆诗松.贝叶斯统计[M].北京：中国统计出版社，2008.

[3]Geman S,Geman D.Stochastic relaxation,Gibbs distribution and the Bayesian restoration of images[J].IEEE Tansactions on Pattern Analysis and Mechine Intelligence,1984,6:721～741.

[4]Gelfand A E,Smith A F M.Sampling based on approaches to calculating marginal densities[J].Journal of American Statistical Association,1990,85(2):339～355.

[5]莫惠栋.农业试验统计[M].上海：上海科学技术出版社，1984.