一种不确定性数据中最大频繁项集挖掘方法

汪金苗, 张龙波， 闫光辉， 王凤英

(1.山东理工大学 计算机科学与技术学院， 山东 淄博 255091；2.兰州交通大学 电子与信息工程学院， 甘肃 兰州 730070)

不确定性数据广泛存在于多个应用领域中，例如RFID(Radio Frequency Identification)，LBS (Location Based Services)，传感器网络等，其特点是每个数据对象不再是传统的单个数据点，而是按照概率分布在多个数据点上[1].目前对不确定性数据挖掘算法的研究已经成为了数据挖掘领域的新热点.不确定性数据挖掘主要包括分类、聚类、孤立点检测、频繁项集挖掘等方面，其中频繁项集挖掘是重点研究的问题之一.

文献[2]在Apriori算法的基础上提出了适用于不确定数据挖掘的U-Apriori算法，文献[3]在FP-growth算法的基础上提出了基于树结构的不确定数据频繁项集挖掘算法UF-growth，文献[4-6]进一步在此基础上提出了包含约束条件的频繁项集挖掘算法，文献[7]综述了不确定性数据中的频繁项集挖掘算法，文献[8]在基于约束的频繁项集挖掘算法U-FPS的基础上，提出了一种不确定性数据中基于约束的频繁项集挖掘算法，其支持度的计算采用数据库垂直模式求交集的方式.文献[9]提出了一种不确定性数据中频繁项的查询算法，通过两条过滤规则来减少检测数据的数量，从而提高查询精度.

目前，不确定性数据中最大频繁项集的挖掘算法尚不多见，在此背景下本文提出一种不确定性数据中最大频繁项集挖掘算法UMF-growth(Uncertain Maximal Frequent-growth)，该算法以UF-growth算法为基础，可通过两个步骤完成最大频繁项集的挖掘：(1)获取所有的频繁1-项集，进而挖掘出以所有频繁1-项集为后缀的局部最大频繁项集；(2)在UMF-tree的帮助下，从第(1)步得到的局部最大频繁项集中挖掘出所有全局最大频繁项集.

1 问题定义

在不确定性数据中，数据集D由d个事务t1,t2,…，td构成，每个事务ti由多个项构成，多个项的集合可用X来表示，每个项x在ti中出现的概率用P(x,ti)来表示.一个项集X出现在现实世界的概率(预计支持度except support)是通过将X出现在每个可能世界Wj的支持度相加得到的.用expSup(X)表示X出现在现实世界的预计支持度，可能世界Wj出现的概率用P(Wj)表示，X出现在可能世界Wj的概率用S(X,Wj)表示，则有如下公式：

P(Wj)=

(1)

expSup(X)=

(2)

如果一个由不确定性数据构成的频繁项集Y的所有超集都是非频繁项集，则称Y为最大频繁项集，所有的最大频繁项集记为UMF(Uncertain Maximal Frequent)；在挖掘过程中得到的、以某个项y为后缀的最大频繁项集称为y的局部最大频繁项集，记为y-LUMF(Local Uncertain Maximal Frequent).

2 不确定性数据中最大频繁项集挖掘算法UMF-growth

与UF-growth算法类似，我们提出的UMF-growth算法也是首先构建UF-tree，然后借助UF-tree进行最大频繁项集的挖掘.UF-tree的每个节点包括三个字段：(1)项的名称(2)预计支持度(3)预计支持度相等的同一个项出现的次数count.其构建过程如下：

(a)扫描整个事务数据库，分别将每个项的支持度进行相加，结果(该项的预计支持度)不小于阈值的项记为频繁1-项集，按照累加的预计支持度对所有的频繁1-项集降序排序，结果保存在L中.

(b)类似与FP-tree的构建过程，再一次扫描事务数据库，将每条事务中的频繁1-项集按照L中的顺序进行排序，然后插入到UF-tree中，同时舍弃非频繁项，当数据库中所有包含频繁1-项集的事务均插入到UF-tree中后即完成了UF-tree的构建.UF-tree的构建过程与FP-tree的不同之处在于，当要插入某条事务时，当且仅当该事务包含的所有项的名称及预计支持度依次与UF-tree中已有的某个分支上的项名及预计支持度完全一致时，该事务可以与这个分支合并，同时每个节点的count加1；如果即将插入的事务所包含的项与某个分支不完全一致，或者项名一致而某些项的预计支持度不一致，则该事务都要作为UF-tree的一个新的分支插入进来.

完成UF-tree的构建后就可以进行最大频繁项集的挖掘了.UMF-growth算法将挖掘过程分为两个步骤，(1)采用LUMF-growth(Local Uncertain Maximal Frequent-growth)挖掘所有以频繁1-项集为后缀的局部最大频繁项集；(2)利用所有的局部最大频繁项集构建UMF-Tree，从而挖掘出所有的全局最大频繁项集，即真正的最大频繁项集.

2.1 局部最大频繁项集挖掘算法LUMF-growth

UF-tree构建完成后，从L中的最后一个项x(即支持度最小的频繁1-项集)开始，遍历UF-tree，找出所有包含x的分支，这些分支即表示以x为后缀的局部最大项集(不一定是频繁的).局部最大项集可能有多个，设其中的一个为{X,x}，其中X包含k个项，x在此分支上的频数count为n，计算项集{X,x}的预计支持度，根据不同的结果分两种情况处理：

(1)如果得到的预计支持度不小于最小支持度阈值min_sup，即项集{X,x}是频繁的，则将{X,x}记为以x为后缀的局部最大频繁项集x-LUMF.同时按以下方法对UF-tree进行剪枝操作：如果项集{X,x}包含该分支上的所有节点，则将这些节点的频数count减n(即减去已参与计算的部分)，如果某些节点的count减为0，则将其剪枝.进行剪枝的原理为：由于x是支持度最小的项，所以x必定位于UF-tree的叶子节点，这样x-LUMF就包含了该分支上的所有节点，以该分支上其他节点为后缀的局部最大频繁项集一定是x-LUMF的子集，因此都不可能是最大频繁项集，所以将其进行剪枝.

(2)如果得到的预计支持度小于支持度阈值min_sup，则对X生成包含k-1个项的子项集{X1,X2,…，Xk}，然后分别计算{X1,x}，{X2,x}，…，{X,x}的预计支持度.对于{X1,x}，如果其预计支持度不小于阈值min_sup，则按步骤(1)进行处理；否则，继续对X1生成包含k-2个项的子项集，然后按同样的方式处理，直到找到以x为后缀的局部最大频繁项集或者子项集为空.

重复步骤(1)与(2)，直到找到所有的x-LUMF，然后将UF-tree中所有包含x的节点删除，对L中倒序排序的下一个频繁1-项集按同样的方式进行处理，直到UF-tree为空.此时即得到了所有以频繁1-项集为后缀的局部最大频繁项集.

算法的伪代码如下：

(Ⅰ)LUMF_growth(UF-tree,Header)

输入：当前的UF-tree，头表Header

输出：所有的局部最大频繁项集

(1)forHeader中最后一个节点x的每个路径{X,x}

(2)if (expSup{X,x}>=min_sup)

(3)x.LUMF=x.LUMF∪X

(4)ifX包含该路径上的所有节点

(5) for每个节点β

(6)β.count=β.count-checkCount；

//checkCount指该节点参与计算的频数

(7) if(β.count=0)

(8)Remove(β)；

//如果频数减为0则将该节点删除

(9)else

(10)getMFSubset(UF-tree，{X,x})；

(11)Remove(x)；//将节点x从UF-Tree删除

(12)Delete(x)；//将x从Header中删除

(13)LUMF_growth(UF-tree,Header)；

(Ⅱ)getMFSubset(UF-tree，{X,x})

输入：当前的UF-tree，项集 {X,x}

输出：项集{X,x}的所有最长频繁子项集

(1)k=getNodenum(X)；//获得集合X包含的节点数

(2)if (k>1)

(5) if(expSup{Xi,x}>=min_sup)

(6)x.LUMF=x.LUMF∪Xi；

(7) return( )；

(8) else

(9)getMFSubset(UF-tree，{Xi,x})；

2.2 最大频繁项集的挖掘

完成局部最大频繁项集的挖掘后，通过构建UMF-tree的方式来进行最大频繁项集的挖掘.UMF-tree的构建过程与FP-tree类似，从L中的最后一个项、倒序开始(即按预计支持度从小到大的顺序)，将每个以频繁1-项集为后缀的局部最大频繁项集作为UMF-tree的一个分支，但是在插入之前需要检查UMF-tree中是否存在某个分支已包含该项集，如果存在这样的分支，则说明UMF-tree中存在该局部最大频繁项集的超集，则该项集就不可能是最大频繁项集，将其舍弃，否则，按照FP-tree的构建方式插入到UMF-tree中.对所有的局部最大频繁项集进行如上操作，最后得到的UMF-tree即包含了所有的最大频繁项集.

根据局部最大频繁项集的挖掘方式以及UMF-tree的构建方式可以得出如下结论：将要插入到UMF-tree的局部最大频繁项集，要么是UMF-tree中某个分支的子项集，要么是全局最大频繁项集，而不会是在其之后插入的局部最大频繁项集的子项集.这是因为，进行局部最大频繁项集挖掘时，是从L中的最后一个项开始、倒序进行的，也就是按频繁1-项集的预计支持度从小到大的顺序进行的，这样得到的局部最大频繁项集是按照其后缀在L中的顺序倒序排列的；而UMF-tree的构建也是从L中的最后一个项开始、倒序进行的，由局部最大频繁项集的挖掘方法可知，先进行插入操作的局部最大频繁项集的后缀项，肯定不会出现在之后插入的局部最大频繁项集中，即先插入的局部最大频繁项集不可能是后插入的局部最大频繁项集的子项集，而只能是其超集，所以可以得出上述结论.

根据这个结论得知：UMF-tree包含且仅包含了数据库中的所有最大频繁项集，其每个分支即为一个最大频繁项集.

3 实验与分析

IBM数据生成器(IBM Quest Market-Basket Synthetic Data Generator)是数据挖掘领域常用的一种数据生成工具，本实验中所使用的数据集也是由该数据生成器生成.我们生成的事务数据库中共含有1 000种项，包含100k条事务，平均事务长度为10，实验进行之前，先对每条事务中的每个项设置一个随机概率作为该项的支持度，其范围为 (0,1].实验环境为CPU Intel core×2，内存2G，操作系统为LINUX，算法采用C语言编写，算法运行时间包括CPU消耗时间及I/O时间，实验数据均是多次测试得到的平均值.

由于目前对不确定性数据的挖掘大都集中在完全频繁项集，而尚未发现最大频繁项集挖掘算法，因此无法进行实验结果的对比.我们分别设计了4个实验来对UMF-growth算法的各项性能进行测试，包括最小支持度阈值对算法性能的影响、算法的可伸缩性、数据集的稠密情况对算法性能的影响以及同一个项名不同支持度个数对算法性能的影响，并对每个实验的结果进行了解释与分析.

在第一个实验中，测试了支持度阈值对算法性能的影响，如图1所示.UMF-growth算法的运行时间随支持度阈值的增大而逐渐增加，这是因为，当支持度阈值较小时，最大频繁项集长度较大，在局部最大频繁项集挖掘过程中不用生成子项集，所以挖掘时间较少.随着支持度阈值的增加，最大频繁项集的长度越来越小，在局部最大频繁项集挖掘过程中需要不断生成这些非频繁项集的子项集，所以挖掘时间随支持度阈值的增加而增加.在实验过程中发现，UMF-growth算法的时间消耗大都集中在局部最大频繁项集的挖掘部分，而UF-tree及UMF-tree的构建时间所占比重较小，因此总体时间随支持度阈值的增大而增加.

第二个实验测试的是UMF-growth算法的可伸缩性.这个实验中不仅要用到包含100KB个事务的数据集，还要用到另外9个不同规模的数据集，其规模大小为10KB，10KB，20KB，30KB，40KB，50KB，60KB，70KB，80KB和90KB.对这10个规模不同的数据集分别利用UMF-growth算法进行最大频繁项集的挖掘，其中支持度阈值设为0.1，得到的结果如图2所示.UMF-growth算法的运行时间随数据库规模的增大几乎成线性增长，这说明UMF-growth算法具有良好的可伸缩性.

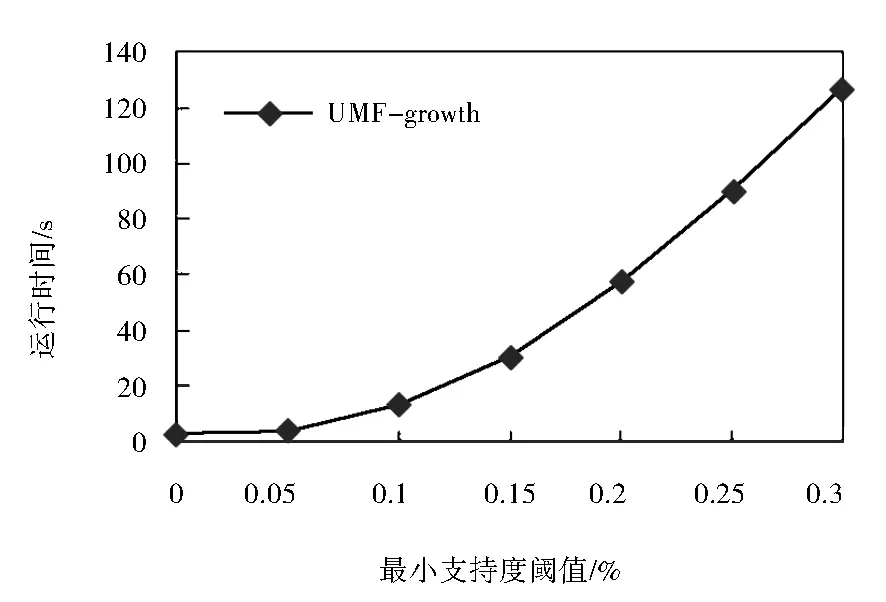
图1 运行时间随阈值的变化

图2 运行时间随数据集规模的变化

第三个实验进行了数据集稠密程度对算法性能的影响测试.一个数据集的参数主要包含项的个数、事务个数、平均事务长度以及最大频繁项集平均长度等.若某数据集的最大频繁项集平均长度与平均事务长度相差很小，则认为该数据集属于稠密型，否则认为该数据集属于稀疏型.数据集的稠密程度往往会对算法的性能产生较大影响.选取两个稠密程度不同的数据集对UMF-growth算法的性能进行测试，观察在不同的数据集上UMF-growth算法运行时间的大小及其随支持度阈值的变化情况，这两个数据集的参数如表1所示，其中D1为稀疏型数据集，D2为稠密型数据集，实验结果如图3所示.UMF-growth算法在D1上的运行时间总是长于在D2上的运行时间.这是因为D1属于稀疏型数据集，其最大频繁项集平均长度远远小于平均事务长度，所以在挖掘过程中总是要产生非频繁项集的子项集，子项集的生成消耗时间较长，导致挖掘时间较长；而数据集D2属于稠密型数据集，其最大频繁项集的长度与平均事务长度一致，在挖掘过程中可直接得到局部最大频繁项集，无需产生子项集，所以挖掘时间较短.通过这个实验可以得知，UMF-growth算法特别适用于平均事务长度较短、比较稠密的数据集.

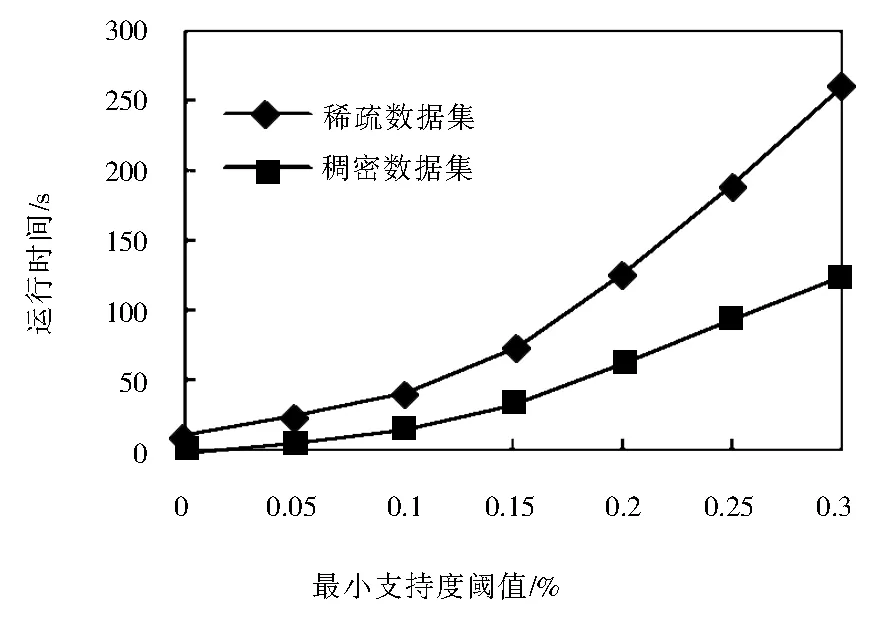
图3 稀疏数据集VS.稠密数据集

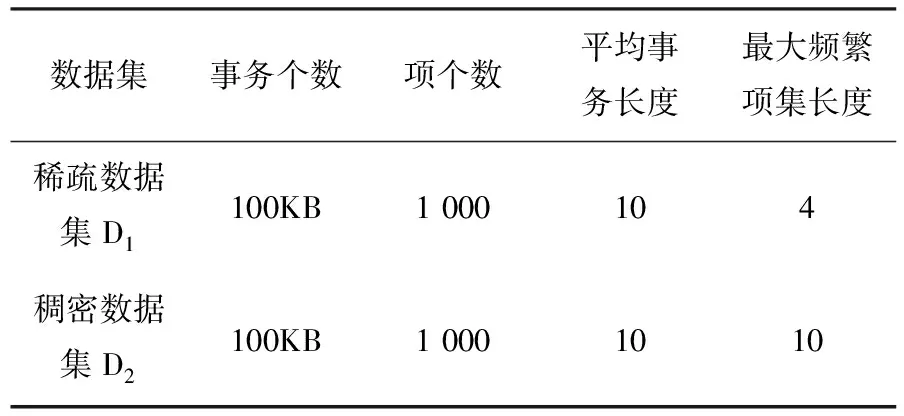
数据集事务个数项个数平均事务长度最大频繁项集长度稀疏数据集D1100KB1 000104稠密数据集D2100KB1 0001010

在最后一个实验中同一项名的不同支持度个数对算法性能的影响进行了测试.本实验采用两个规模及参数都相同的数据集，分别将其同一项名的不同支持度个数设置为较多个和较少个，对UMF-growth算法在这两个数据集上的运行时间进行对比，实验结果如图4所示.由图可知，UMF-growth算法在具有较多支持度个数的数据集上的运行时间要长于在具有较少支持度个数的数据集上的运行时间.这是因为，在构建UF-tree时我们规定，只有当项名相同且支持度相同的情况下，两个分支才可以合并，当项名相同而支持度不同时，需要作为不同的分支插入到UF-tree中，此时UF-tree的规模会增大，UMF-growth的运行时间会增加，所以具有较少支持度个数的数据集中分支可合并的概率更大，UF-tree的规模更小，运行时间较短.

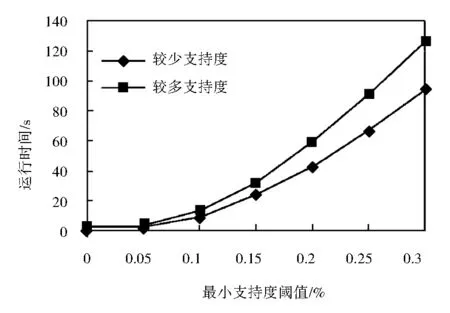
图4 较少支持度VS.较多支持度

由以上4个实验可知，UMF-growth算法的运行时间随支持度阈值的增加而增加，同一项名支持度个数较少时效率较高，具有良好的可伸缩性并且特别适用于稠密型数据集.但是该算法也存在一些不足，例如在LUMF-growth步骤中需要不断的产生非频繁项集的子项集，当事务平均长度较大且比较稀疏时，生成子项集需占用大量内存、消耗大量时间，因此UMF-growth算法在稀疏型数据集上的效率还有待进一步提高.

4 结束语

本文提出的基于UF-tree的最大频繁项集挖掘算法UMF-growth算法，是通过两个步骤完成最大频繁项集的挖掘，首先在UF-tree的基础上获得局部最大频繁项集，然后将局部最大频繁项集插入UMF-tree中获得所有的最大频繁项集.实验结果证明，UMF-growth算法具有良好的可伸缩性且特别适用于稠密型数据集，尤其是那些平均事务长度较短或最大频繁项集长度与平均事务长度接近的数据集.但是，UMF-growth算法在稀疏型数据集，特别是平均事务长度较大的数据集中效率较低，因此该算法的效率还有待进一步优化提高.

[1]Leung C K S. Mining uncertain data[J]. Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery, 2011, 1(4): 316-329.

[2]Chui C K, Kao B, Hung E. Mining frequent itemsets from uncertain data[M]. Advances in knowledge discovery and data mining.Heidelberg:Springer Berlin, 2007: 47-58.

[3]Leung C K S, Mateo M A F, Brajczuk D A. A tree-based approach for frequent pattern mining from uncertain data[M]. Advances in Knowledge Discovery and Data Mining. Heidelberg:Springer Berlin, 2008: 653-661.

[4]Leung C K, Brajczuk D A. Efficient algorithms for the mining of constrained frequent patterns from uncertain data[J]. SIGKDD Explorations, 2010, 11(2):123-130.

[5]Cuzzocrea A, Leung C K. Distributed mining of constrained frequent sets from uncertain data[C]//Algorithms and Architectures for Parallel Processing. Springer Berlin Heidelberg, 2011: 40-53.

[6]Leung C K S, Sun L. Equivalence class transformation based mining of frequent itemsets from uncertain data[C]// Proceedings of the 2011 ACM Symposium on Applied Computing. ACM, 2011: 983-984.

[7]汪金苗, 张龙波, 邓齐志，等．不确定数据频繁项集挖掘方法综述[J]. 计算机工程与应用, 2011, 47(20):121-125．

[8]刘卫明，杨健，毛伊敏．基于约束的不确定数据频繁项集挖掘算法研究[J].计算机应用研究，2012, 29(10): 3 669-3 671．

[9]王爽, 杨广明, 朱志良．基于不确定数据的频繁项查询算法[J].东北大学学报：自然科学版，2011, 32(3): 344-347