分子相互作用体积模型在真空蒸馏分离Pb-Sb、Pb-Ag和Sb-Cu合金中的应用

孔令鑫 ，李一夫 ，杨 斌 ，徐宝强 ，刘大春 ，戴永年

1.昆明理工大学 真空冶金国家工程实验室，昆明 650093；2.昆明理工大学 云南省有色金属真空冶金重点实验室，昆明 650093；3.昆明理工大学 云南省复杂有色金属资源清洁利用国家重点实验室(培育基地)，昆明 650093)

合金分离的传统处理方法存在流程长、能耗高、产量低、经济效益差等问题[1]，真空冶金作为冶金领域的新技术，与传统冶金方法相比具有工艺流程简单、金属回收率高、资源和能耗消耗少、无废水废气产生等优点，广泛应用于合金的分离和粗金属的精炼[2−7]。昆明理工大学多年来一直进行合金分离的小型、扩大及工业化试验，取得了很好的效果，但理论基础研究工作较少。

活度是冶金过程中重要的热力学数据，然而通过实验研究热力学性质具有许多困难[8−10]，尽管实验技术近年来也有了突飞猛进的发展，但该类实验是高温实验，温度的获得有一定的难度；其次，温度的准确检测具有一定难度；再者，其费用也很昂贵，所以实验本身的困难和复杂性成为获取热力学性质的主要制约因素。因此，利用理论或半经验数学模型对溶液的热力学性质进行预测，并对现有热力学数据进行拟合就显得尤为重要。近百年来，许多研究者从不同角度提出了诸多模型，如正规溶液模型(Regular solution model)[11]、亚正规溶液模型(Sub-regular solution mode)[12]、准正规溶液模型(Quasi-regular solution model)[13]、Wilson方程[14]和新一代几何模型[15]，但各模型都有一定的适用条件和局限性，如Wilson方程的突出特点是通常对极性和非极性混合物组元活度系数的出众表达(对有正偏差的体系拟合非常好)，但不能处理不混溶性溶液，对有较小负偏差的体系拟合效果不好[16]。

基于自由体积理论和晶格理论，结合统计热力学和流体相平衡理论，TAO[17]提出了分子相互作用体积模型(Molecular interaction volume model，MIVM)，其物理基础清晰、可靠，且只需二元系无限稀活度系数实验数据即可计算合金中各组元的活度。为此，本文作者采用MIVM计算Pb-Sb、Pb-Ag及Sb-Cu合金中各组元的活度和活度系数，并进一步计算合金各组元在真空蒸馏过程中的气液相平衡组成，进而判断真空蒸馏分离合金的可能性与分离程度。

1 分子相互作用体积模型

分子相互作用体积模型[17]是基于统计热力学推导得到，具有清晰的物理基础，其预测效果在之前的研究中已有证实，具体详见文献[17]。根据 MIVM，固溶体i−j的摩尔过量吉布斯自由能可表示为

其中：Zi表示最邻近分子数或第一配位数；xi和xj分别表示i和j的摩尔分数；Vsi和Vsj分别表示纯固体i和j的摩尔空隙；λi和λj分别表示固体i和j的空隙数；Bij和Bji表示对势能相互作用参数，并将其定义为

式中：εii、εjj和 εij分别表示 i−i、j−j和 i−j的对势能，且εij=εji；k表示波尔兹曼常数；T是热力学温度。

对于固态合金i−j二元系，参数Bij和Bji可由组元i、j的无限稀活度系数实验数据求得。Pb-Sb、Pb-Ag和Sb-Cu体系的无限稀活度系数实验数据[18]列于表1。

当 xi→0时，由式(3)可得到该二元系中组元 i的无限稀活度系数的表达式：

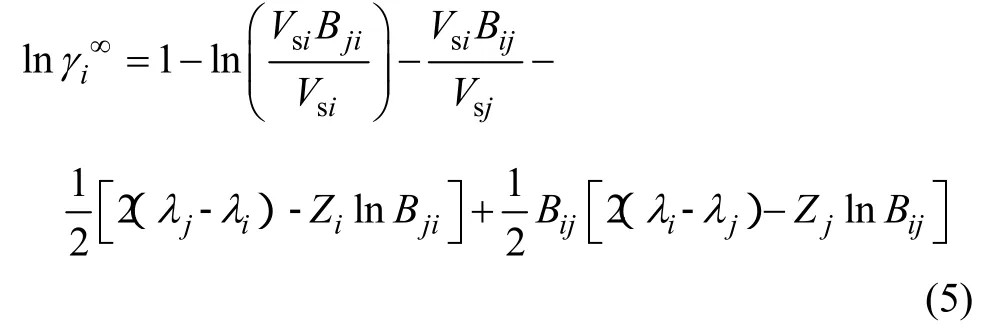
同理，当 xj→0时，由式(4)可得到该二元系中组元j的无限稀活度系数的表达式：

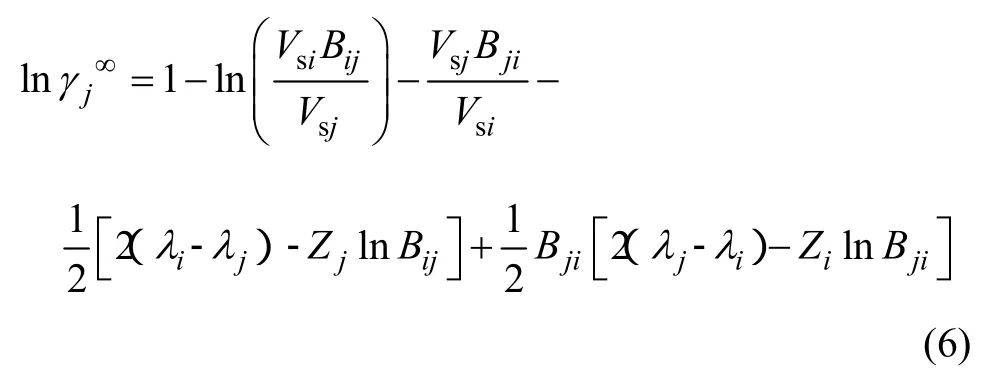
联立方程(5)和(6)，可求得参数Bji和Bij，令

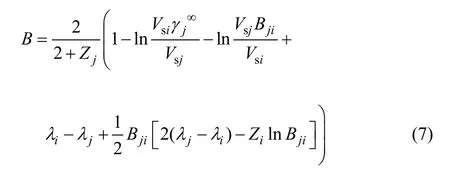
则

将式(8)代入式(5)，并令

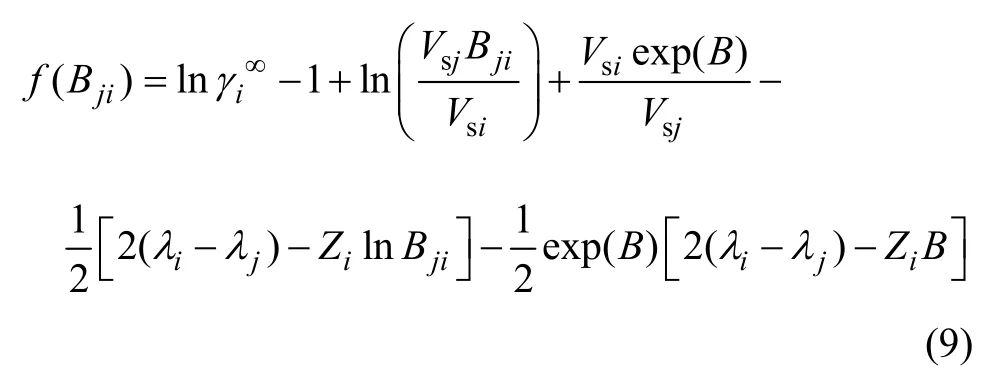
函数f(Bji)的导数：

其中

由牛顿迭代公式可得

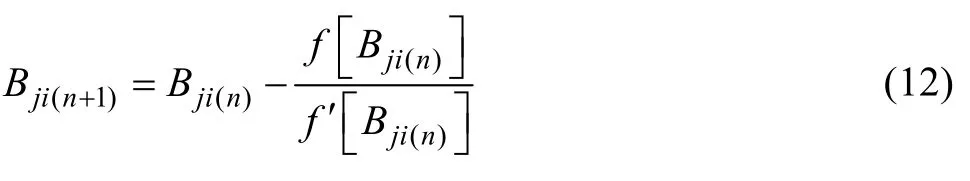
因此，由固态合金二元系的无限稀活度系数实验数据 γi∞和 γj∞及纯金属相关参数，经过(n+1)次迭代后，直到为所需精度，本研究选取ε =10−8)，即可得到该精度下的Bji和Bij参数值，纯金属的相关参数[19−20]列于表2，Bji和Bij计算结果见表1。表2中的Vmi、ΔHmi、σi、r0i分别表示纯固体i的摩尔体积、熔化焓、原子钢球直径和原子半径。

另外，若已知某一温度(T1)下Bij和Bji的参数值，并 且 假 设 对 势 能 相 互 作 用 参 数 (εij−εjj)/(kT)和(εji−εii)/(kT)与温度无关，则 Bij和 Bji在所需温度(T2)下的参数值可由式(2)计算得到，即

表1 不同温度下二元合金 i−j 的 γi∞、γj∞、Bij和 Bji参数值[18]Table 1 Values of and Bji of binary alloys i−j at different temperatures[18]

表1 不同温度下二元合金 i−j 的 γi∞、γj∞、Bij和 Bji参数值[18]Table 1 Values of and Bji of binary alloys i−j at different temperatures[18]

i−j T/K γi∞ γj∞ Bij Bji Zi Zj Pb-Sb 905 0.779 0.7791.014 7 1.027 5 10.29 8.74 Pb-Ag1 2730.924 2.0311.067 0 0.811 6 9.55 11.19 Sb-Cu1 190 0.028 0.3781.417 6 0.632 4 6.92 11.84

表2 合金组元的相关参数[19−20]Table 2 Related parameters of components[19−20]

2 分子相互作用体积模型在真空蒸馏过程中的应用

真空蒸馏分离合金过程中，定量估算出一定温度下气液相中各组元的百分含量以及合金分离程度，对实验和生产都有重要的指导意义，气液相平衡图的绘制即可达到此目的。

对于i−j二元合金，组元i、j在气相中的质量分数分别用ωi,g、ωj,g表示，液相中用ωi,l、ωj,l表示，则有

气相：

液相：

则组元 i在气相中的质量分数 ωi,g可用两组元的蒸汽密度ρ[21]表示：

这里，

式中：βj为组元 j的分离系数；pi*和 pj*分别为组元 i和j的纯物质饱和蒸汽压。

将式(18)和(19)代入式(17)得

式中：ω和γ分别代表合金中组元的质量分数和活度系数。

ωi,g—ωi,l在一定温度下的关系图可使用 P*、γ及一系列的ωj,l/ωi,l计算得到，即i−j体系气液相平衡组分图。Pb-Sb、Pb-Ag及Sb-Cu体系中各组元的纯物质饱和蒸汽压[21]列于表3。

表3 不同温度下合金组分的蒸汽压[21]Table 3 Vapor pressures of components of alloys at different temperatures[21]

3 结果与讨论

3.1 活度

将上面计算得到的对势能相互作用参数 Bij和 Bji及相关参数代入式(3)和(4)，即可计算出Pb-Sb、Pb-Ag及Sb-Cu合金中各组元的活度，并将活度计算值和实验值[22]进行比较，其结果如图1所示。

从图1(a)中可看出，在Pb-Sb体系中，Pb与 Sb的活度计算值和实验值在全成分范围内吻合较好。从图1(b)中可看出，Pb-Ag体系中，当Pb含量在0.1～0.3范围内时，Pb的活度计算值和实验值吻合稍差，而Ag的吻合较好，然而当Pb含量在0.3～1.0范围内时，Pb的活度计算值和实验值吻合较好，而Ag的吻合稍差。从图1(c)中可看出，Sb-Cu体系在全成分范围内，Sb的活度计算值和实验值吻合较好，而Cu的吻合稍差。以上分析表明分子相互作用体积模型用于预测Pb-Sb、Pb-Ag及Sb-Cu二元合金体系的活度具有较高的准确性，另外，分子相互作用体积模型是基于统计热力学推导得出，其物理基础清晰，且只需无限稀活度系数实验数据即可计算合金体系的活度及活度系数，说明分子相互作用体积模型用于预测 Pb-Sb、Pb-Ag及Sb-Cu二元合金体系的活度具有较高的稳定性和简便性。该方法可能会有一定误差，原因可能来源于实验技术条件及实验数据的精确性有限，另外，误差也可能来源于该计算模型。

3.2 活度系数

将计算得到的活度代入式(21),即可计算得到Pb-Ag、Sb-Cu及Pb-Sb合金体系的活度系数，结果分别如表4～6所示。

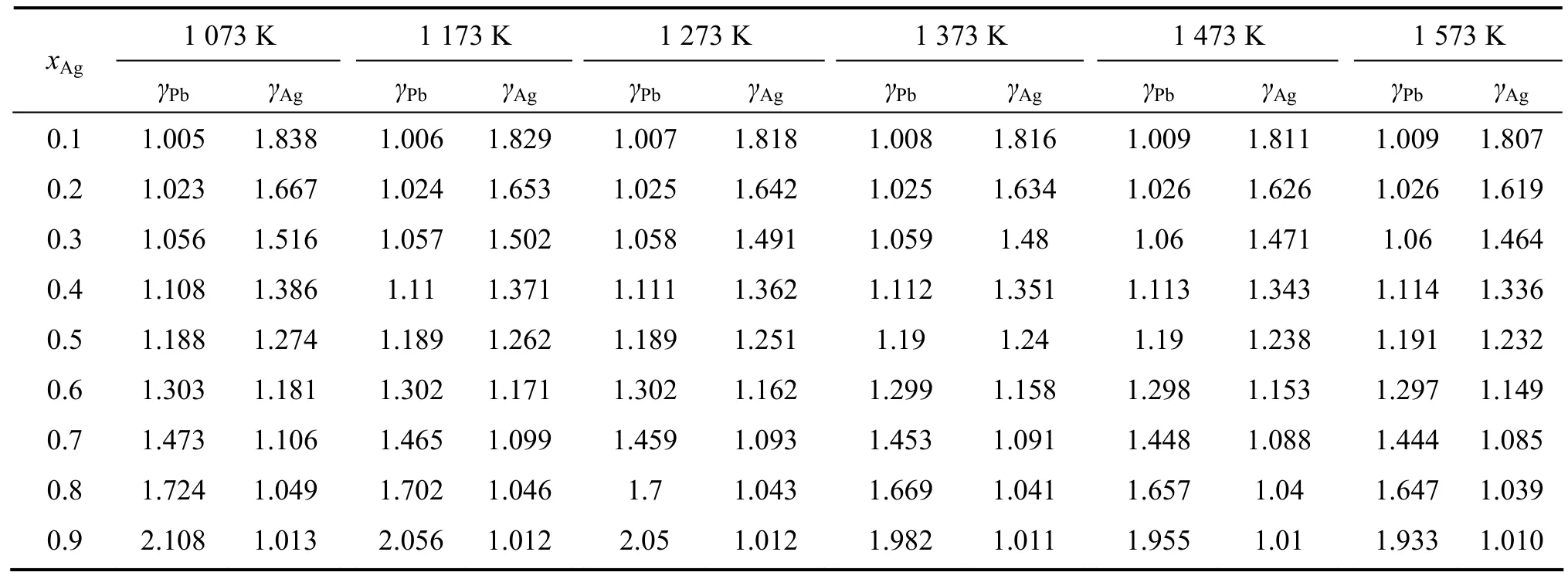
表4 Pb-Ag合金体系不同温度下的活度系数Table 4 Activity coefficients of Pb-Ag alloy system at different temperatures

从表4可知，Pb-Ag体系中，在温度恒定的条件下，随着Ag含量的升高，Ag的活度系数逐渐减小，Pb的活度系数不断增大；当Ag含量在0.1～0.5范围内，且保持不变时，Pb的活度系数随着温度的升高不断增大；当Ag含量在0.6～0.9范围内，随着温度升高不断减小，而 Ag的活度系数在全成分范围内均是随着温度升高不断减小；在800～1 300 ℃时，全成分范围内，Pb和Ag的活度系数都大于1。从表5可知，在温度恒定的条件下，随着Cu含量的升高，Cu的活度系数逐渐增大，Sb的活度系数不断减小；当组元含量不变时，随着温度的升高，Sb的活度系数不断增大，Cu的活度系数不断减小；在800～1300 ℃时，全成分范围内，Sb和Cu的活度系数均小于1。从表6可知，Pb-Sb体系中，在温度不变的条件下，随着体系中Pb含量的升高，Pb的活度系数不断增大，Sb的活度系数不断减小，但变化都很小；当组元含量不变时，Pb和Sb的活度系数随温度变化都很小。

表5 Sb-Cu合金体系不同温度下的活度系数Table 5 Activity coefficients of Sb-Cu alloy system at different temperature

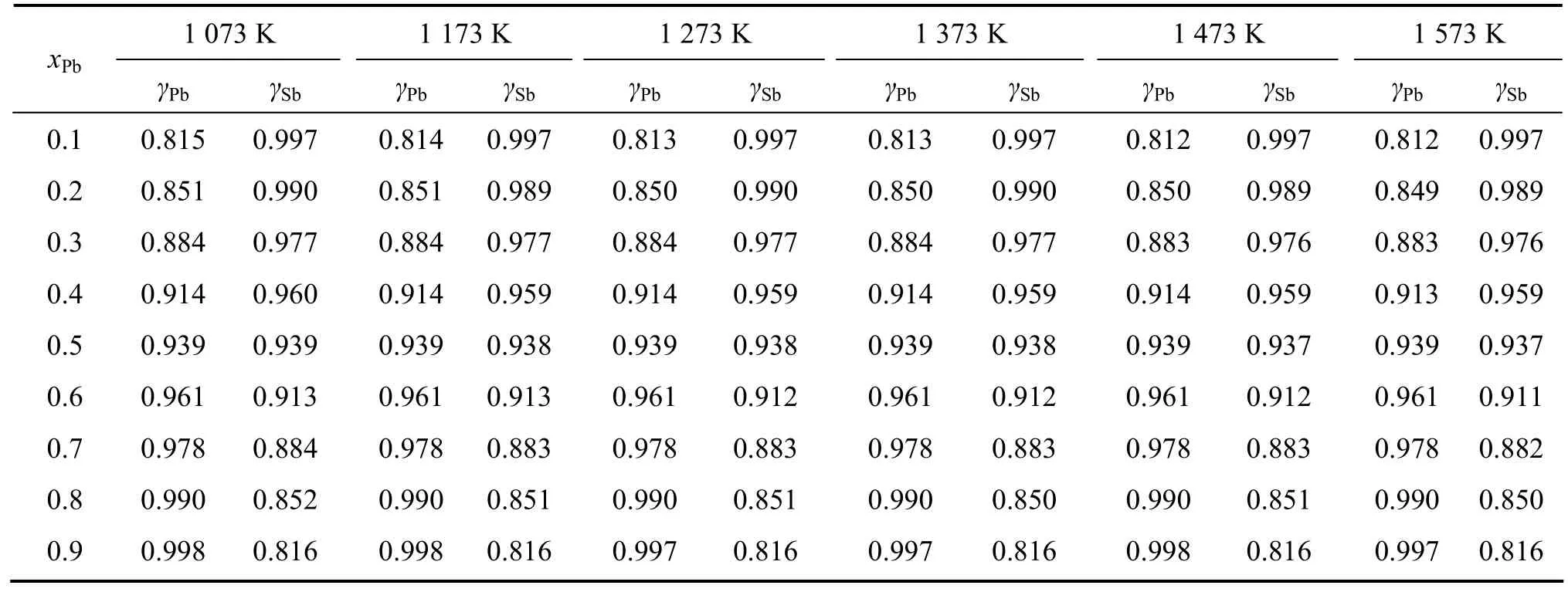
表6 Pb-Sb合金体系不同温度下的活度系数Table 6 Activity coefficients of Pb-Sb alloy system at differnet temperatures

3.3 气液相平衡

为了定量判断Pb-Sb、Pb-Ag及Sb-Cu合金体系在真空蒸馏过程中各组元在气液相中的分布情况及合金分离效果，将计算得到的活度系数及相关参数代入式(20)，可计算得到Pb-Sb、Pb-Ag及Sb-Cu合金体系在不同温度下的气液相平衡组成，结果如图2所示。

从图2 (a)中可看出，随着液相中Ag含量的增加及蒸馏温度的升高，气相中 Ag含量不断增大，这是由于随着温度升高，Ag的蒸汽压不断增大，导致Ag也开始部分挥发，但在1 200 ℃及液相中Ag含量增大到0.9条件下，气相中Ag含量仍远低于0.1，由此说明，真空蒸馏过程中Ag富集于液相，而Pb则挥发进入气相，并冷凝，上述分析表明Pb、Ag可通过真空蒸馏实现良好分离。从图2(b)可看出，随着液相中Cu含量的增大和蒸馏温度的升高，气相中 Cu含量也不断升高，同样是由于温度升高，Cu的蒸汽压不断增大，从而开始挥发进入气相，在1 200 ℃，液相Cu含量为0.9的条件下，气相中Cu含量远低于0.01，说明蒸馏过程中Cu在液相中富集，Sb挥发进入气相冷凝，上述表明Sb、Cu可通过真空蒸馏实现分离。从图2(c)可知，随着液相中Pb含量的增加及蒸馏温度的升高，气相中 Pb含量不断增大，同样是由于温度升高，Pb的蒸汽压不断增大，Pb也开始大量挥发进入气相，另外，由于Pb、Sb的饱和蒸汽压差别很小，导致Sb挥发的同时，Pb也开始大量挥发，所以在1 200 ℃，当液相中Pb含量为0.9时，气相中Pb含量达到了0.637，所以一次真空蒸馏很难将 Pb、Sb彻底分离。以上分析结果表明，气液相平衡图可用于定量预测真空蒸馏过程中合金体系各组元的分布情况，还可用于实验前实验条件的选取以及最终产品纯度的预测。

图2 不同温度下的气液相平衡组分图Fig.2 Vapor-liquid phase equilibrium composition at different temperatures∶ (a)Pb-Ag system; (b)Sb-Cu system; (c)Pb-Sb system

4 结论

1)基于MIVM，计算得到Pb-Sb、Pb-Ag及Sb-Cu合金体系中各组元的活度，并将活度计算值和实验值进行对比分析，发现活度计算值和实验值吻合较好。

2)运用 MIVM 计算得到活度系数，并使用活度系数计算了真空蒸馏过程中不同温度下Pb-Sb、Pb-Ag及Sb-Cu体系的气液相平衡组成。

3)对于Pb-Ag 体系，在1 200 ℃，液相中Ag含量为0.9条件下，气相中Ag含量远低于0.1，说明蒸馏过程中Ag在液相中富集，Pb挥发进入气相，表明Pb、Ag能通过真空蒸馏实现良好分离；对于 Sb-Cu体系，在1200 ℃，液相中Cu含量为0.9条件下，气相中Cu含量远低于0.01，说明蒸馏过程中Cu在液相中富集，Sb挥发进入气相，表明Sb、Cu能通过真空蒸馏实现分离；在Pb-Sb体系中，由于Pb与Sb的饱和蒸汽压差别很小，所以真空蒸馏过程中，Sb挥发时，Pb也开始大量挥发，导致Pb与Sb不能通过一次真空蒸馏实现完全分离。

4)分子相互作用体积模型用于预测Pb-Sb、Pb-Ag及Sb-Cu体系的活度及分离效果具有很高的可靠性。

[1]戴永年.铅−锡合金(焊锡)真空蒸馏[J].有色金属∶ 冶炼部分,1977, 9∶ 24−30.DAI Yong-nian.Vacuum distillation of Pb-Sn alloys (solder)[J].Nonferrous Metals∶ Smelting Part, 1977, 9∶ 24−30.

[2]戴永年, 赵 忠.真空冶金[M].北京∶ 冶金工业出版社, 1988∶20−24.DAI Yong-nian, ZHAO Zhong.Vacuum metallurgy[M].Beijing∶Metallurgical Industry Press, 1998∶ 20−24.

[3]何德文, 刘 蕾, 肖羽堂, 周欢年.真空冶金回收废旧锌锰电池的汞和镉试验研究[J].中南大学学报∶ 自然科学版, 2011,42(4)∶ 893−896.HE De-wen, LIU Lei, XIAO Yu-tang, ZHOU Huan-nian.Experimental research on the recycling of mercury and cadmium from the wasted zinc-manganese battery by vacuum metallurgy[J].Journal of Central South University∶ Science and Technology, 2011, 42(4)∶ 893−896.

[4]韩 龙, 杨 斌, 杨部正, 戴永年, 刘大春, 徐宝强.热镀锌渣真空蒸馏回收金属锌的研究[J].真空科学与技术学报,2009(S1)∶ 101−104.HAN Long, YANG Bin, YANG Bu-zheng, DAI Yong-nian, LIU Da-chun, XU Bao-qiang.Research on the recycling of zinc from the hot galvanizing residue by vacuum distillation[J].Journal of vacuum science and technology, 2009(S1)∶ 101−104.

[5]CHEN Wei-liang, YANG Bin, CHAI Li-yuan, MIN Xiao-bo,DAI Yong-nian, YU Xia, ZHANG Chuan-fu.Vacuum distillation refining of crude lithium (Ⅰ)—Thermodynamics on separating impurities from lithium[J].Transactions of Nonferrous Metals Society of China, 2001, 11 (6)∶ 937−941.

[6]徐宝强, 裴红彬, 杨 斌, 刘大春, 曲 涛, 戴永年.真空碳热还原脱除红土镍矿中镁的研究[J].真空科学与技术学报,2011, 31(3)∶ 341−347.XU Bao-qiang, PEI Hong-bin, YANG Bin, LIU Da-chun, QU Tao, DAI Yong-nian.Research on the deprivation of magnesium from the lateritic-nickel-ore by vacuum carbothermic reduction[J].Journal of Vacuum Science and Technology, 2011,31(3)∶ 341−347.

[7]李 亮, 刘大春, 杨 斌, 徐宝强, 唐万启.真空蒸馏铅阳极泥制备粗锑的研究[J].真空科学与技术, 2012, 32(4)∶ 301−305.LI Liang, LIU Da-chun, YANG Bin, XU Bao-qiang, TANG Wan-qi.Research on the preparation of the crude antimony from the lead anode smile by vacuum distillation[J].Journal of Vacuum Science and Technology, 2012, 32(4)∶ 301−305.

[8]YANG Hong-wei, XU Bao-qiang, YANG Bin, MA Wen-hui,TAO Dong-ping.Calculation of phase equilibrium in vacuum distillation by molecular interaction volume model[J].Fluid Phase Equilibria, 2011(3)∶ 78−81.

[9]TAO Dong-ping, LI Deng-fang, YANG Bin.Prediction of the thermodynamic properties of quaternary liquid alloy by modified coordination equation[J].Themochimica Acta, 2002, 383∶45−51.

[10]TAO Dong-ping.Prediction of thermodynamic properties of the C-Fe-Co-Ni solid solutions by binary infinite dilute activity coefficients[J].Materials Science and Engineering A, 2005, 390∶70−75.

[11]HILDEBRAND J H.The activities of molten alloys of thallium with tin and lead[J].Journal of the American Chemical Society,1929, 51(1)∶ 66.

[12]HARFY H K.A “sub-regular” solution model and its application to some binary system[J].Acta Metallurgica, 1953, 1(2)∶202−209.

[13]LUPIS C H P, ELLIOTT J F.Prediction of enthalpy and entropy interaction coefficients by the “central atoms” theory[J].Acta Metallurgica, 1967, 15(2)∶ 265−276.

[14]WILSON G M.Vapor-liquid equilibrium.Ⅺ.A new expression for the excess free energy of mixing[J].Journal of the American Chemical Society, 1964, 86(2)∶ 127−130.

[15]ZHOU Guo-zhi, WEI Shou-kun.A new generation solution model for predicting thermodynamic properties of a multi-component system from binaries[J].Metallurgical and Materials Transactions B, 1997, 28∶ 439−445.

[16]乐启炽, 张新建, 崔建忠, 路贵民.金属合金溶液热力学模型研究进展[J].金属学报, 2003, 39(1)∶ 35−42.LE Qi-chi, ZHANG Xin-jian, CUI Jian-zhong, LU Gui-min.Research development of the thermodynamic model of metallic alloy solution[J].Acta Metallurgical Sinica, 2003, 39(1)∶ 35−42.

[17]TAO Dong-ping.A new model of thermodynamics of liquid mixtures and its application to liquid alloys[J].Thermochim Acta, 2000, 363∶ 105−113.

[18]PREDEL B, BORNSTEIN LANDOLT.Group Ⅳ∶ Physical chemistry[M].Berlin, Heidelberg, New York∶ Springer, 2006.

[19]LIDA T, GUTHRIE R I L.The physical properties of liquid metals[M].Oxford∶ Clarendon Press, 1988.

[20]FERRO R, SACCONE A.Structure of solids[M].Weinheim∶VCH Verlagasgesellschaft, 1993∶ 704−713.

[21]戴永年.有色金属真空冶金[M].北京∶ 冶金工业出版社,1998∶ 110−116.DAI Yong-nian, Vacuum metallurgy of nonferrous metals[M].Beijing∶ Metallurgical Industry Press, 1998∶ 110−116.

[22]HULTGREN R, DESAI P D, HAWKINS D T, GEISER M,KELLEY K K.Selected values of the thermodynamic properties of binary alloys[M].Metals Park, OH∶ American Society of Metals, 1973.