一个半离散非单调核逆向的Hilbert型不等式
2013-12-13杨必成
陈 强,杨必成
(1.广东第二师范学院计算机科学系,广东广州510303;2.广东第二师范学院数学系,广东广州510303)


其中,常数因子π 仍为最佳值.式(1)与式(2)是分析学的重要不等式[1-2],有不少推广应用[3-8]. 关于半离散、非齐次核的Hilbert 型不等式,其零星结果可见文献[1]、[9]. 关于半离散、齐次且单调核逆向的Hilbert 不等式,见文献[10]的具有最佳常数因子的工作:
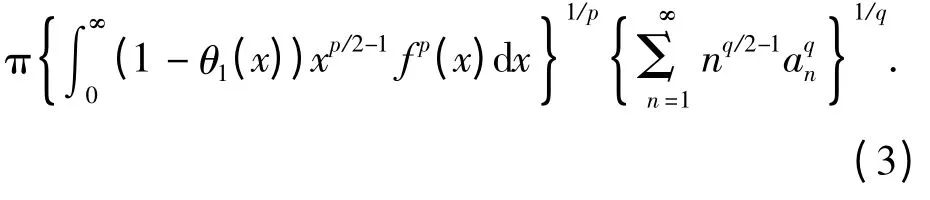
本文应用权系数的方法,建立一个半离散、非单调核逆向的Hilbert 型不等式:设θ1(x)=O(1/x1/2)则有

其中,常数因子8 为最佳值.还考虑了它的引入多参数的最佳推广式与等价式.
1 引理
若f(y)在(0,∞)连续且按段光滑,ρ(y)=y -[y]-1/2 为1 阶Bernoulli 函数,则有
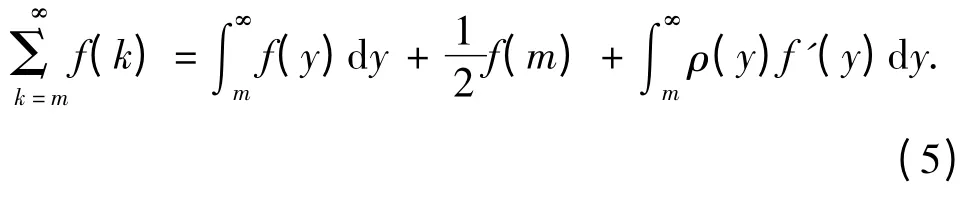


证明 我们有
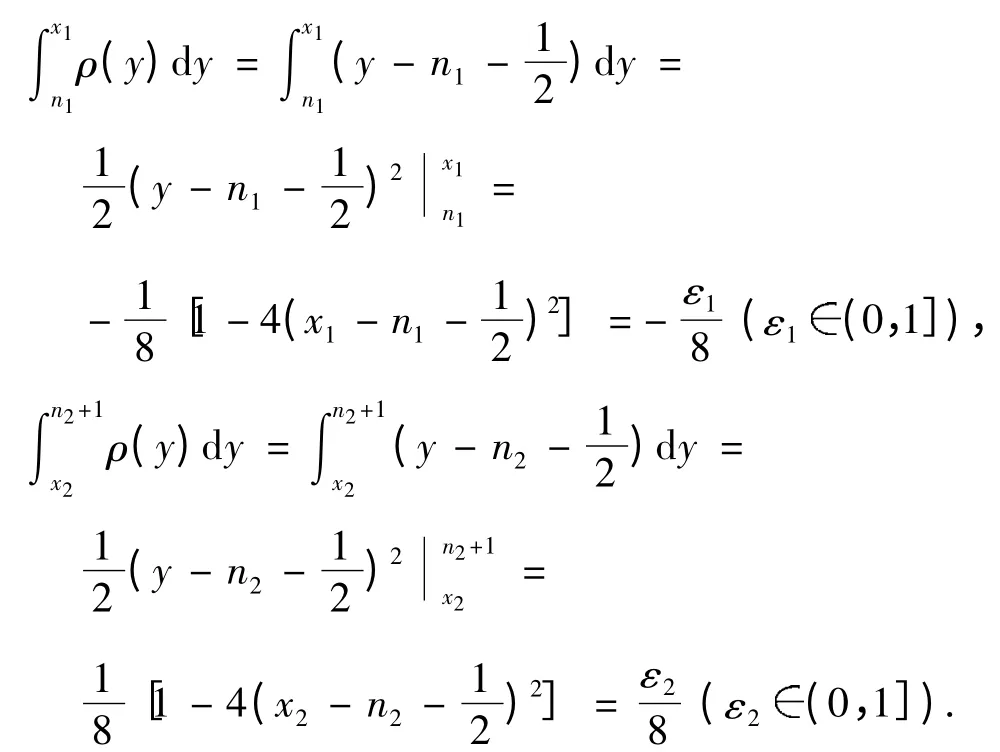
式(7)成立.证毕.
注1 由式(7),对1≤n=[x]≤x,当n≥2 时,有

故有


则有θ(x)>0,θ(x)=O1(1/xλ/r)(x≥1).
证明 (a)令u=y/x,有




定义函数g(y),h(y)如下:

则-f'y(x,y)=g(y)-h(y).设a =(1 -λ)/x2+λ/r,b=(-1 -λ)/x2+λ/r,则a-b=2/x2+λ/r.定义

则因g1(x-0)-a =g2(x),h1(x -0)-a =h2(x),故与(y[1,∞))递减连续,且有由式(6)、(8),有ε1[0,1],εi(0,1)(i=2,3),使

因g1(1)-a≥g1(x -0)-a =g2(x)>0,h1(1)-b≥h1(x-0)-b=h2(x)>0,故由式(10)有


化简可得

故θ(x)>x-λ/rρλ(x)>0 (x≥1).
(b)在式(10)中,我们还有如下逆向不等式及相关结果:故θ(x)=O1(1/xλ/r)(x≥1).证毕.

引理3 在引理1 的条件下,定义如下权函数及权系数:

则有

证明 作变换t=x/n,有

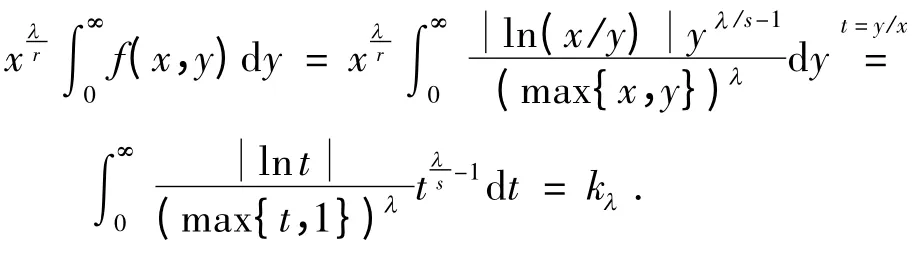
再由式(5)及引理1,有

故式(13)成立.证毕.


证明 由带权逆向的Hölder 不等式[11]及式(11)~(13),有

故式(15)成立. 由逆向的Hölder 不等式[11]及式(11)~(13),注意到q <0,又有

故式(16)成立.证毕.
2 结果

则有如下等价式:

证明 由L 逐项积分定理[12],式(19)中Ⅰ有2种表示.由条件,式(17)不取等号,故有式(20). 由逆向的Hölder 不等式,有

由式(20),有式(19). 反之,设式(19)成立. 取则由式(19),有


由式(17)及条件,知J1>0.若J1=∞,则式(20)自然成立;若J1<∞,则应用式(19)的条件都具备,式(23)取严格不等号,且在式(23)中两边除以J1/q1,有

故式(20)成立,且与式(19)等价.
由条件,式(18)取严格不等号,故有式(21).配方并由逆向的Hölder 不等式,有



由式(18)及条件,知J2<∞.若J2=0,则式(21)自然成立;若J2>0,则应用式(19)的条件都具备,式(25)取严格不等号,且有

两边q(<0)次方,故式(21)成立,且与式(19)等价.故式(19)、(20)与式(21)齐等价.

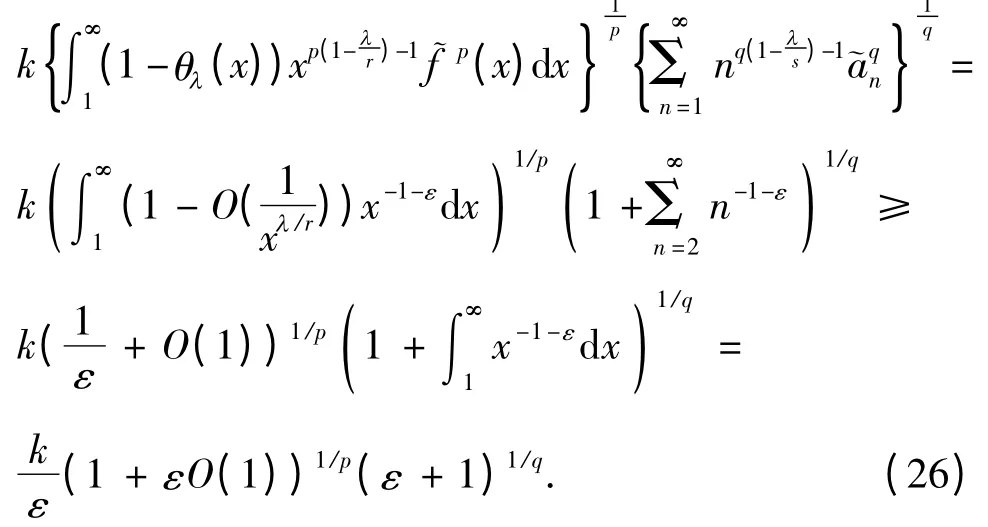

由式(26)、(27),有

故有kλ≥k (ε→0+). 因而k =kλ为式(19)的最佳值.式(20)(式(21))的常数因子必为最佳值,不然,由式(22)(式(24)),必导出式(19)的常数因子也不为最佳值的矛盾.证毕.
评注 (a)当r =s =2,λ =1 时,式(19)变为式(4);式(20)、(21)变为如下与式(4)等价的具有最佳常数因子的半离散非单调-1 齐次核的Hilbert 型不等式:

(b)能否把式(19)~(21)的积分区间拓展为(0,∞),这是一个待解决的公开问题.
[1]HARDY G H,LITTLEWOOD J E,POLYA G. Inequalities[M]. Cambridge:Cambridge University Press,1952.
[2]MINTRINOVICE D S,PECARIC J E,FINK A M. Inequalities involving functions and their integrals and derivatives[M]. Boston:Kluwer Academic Publishers,1991.
[3]YANG Bicheng. On Hilbert's integral inequality[J]. J Math Anal Appl,1998,220:778 -785.
[4]杨必成.算子范数与Hilbert 型不等式[M].北京:科学出版社,2009.
[5]YANG Bicheng. Hilbert-type integral inequalities[M].Dubai:Bentham Science Publishers Ltd,2009.
[6]YANG Bicheng. Discrete Hilbert - type inequalities[M]. Dubai:Bentham Science Publishers Ltd,2011.
[7]KRNIC M,PECARIC J. Hilbert's inequalities and their reverses[J]. Publ Math Debrecen,2005,67(3 -4):315 -331.
[8]AZAR L E. On some extensions of Hardy-Hilbert's inequality and applications[J]. J Inequal Appl,2008,doi:10.1155/2008/546829.
[9]YANG Bicheng. A mixed Hilbert-type inequality with a best constant factor[J]. International Journal of Pure and Applied Mathematics,2005,20(3):319 -328.
[10]杨必成.一个半离散的Hilbert 不等式[M].广东第二师范学院学报,2011,31(3):1 -7.
[11]匡继昌. 常用不等式[M]. 济南:山东科技出版社,2004.
[12]匡继昌. 实分析引论[M]. 长沙:湖南教育出版社,1996.
