树叶长宽比及边缘曲率的提取

王 静，李灿灿，王情伟，王 宝，李丰果

(华南师范大学物理与电信工程学院，广东广州510006)

叶子是植物的重要器官，它直接反映了植物的种类和生长状况.随着计算机技术的发展，图像处理和识别技术在叶片形状、颜色和叶脉等特征参数的提取中得到了广泛的应用［1－9］. 在树叶轮廓方面:JOAO 等［4］提出了提取叶片轮廓特征的链码和椭圆傅里叶谐波函数算法.王晓峰等［5］在获取树叶轮廓的基础上，计算了叶片的矩形度、圆形度和偏心率等几何特征.在树叶面积方面:李宝光等［6］分别利用复印称重法、直尺法、辛普森公式法和数字图像处理法测定了食用仙人掌的面积，并对几种方法进行了比较.王忠芝等［7］建立了叶片长宽和叶片面积的幂函数回归方程，根据叶片长宽估算叶片的面积.在边缘曲率方面:FRANZ 等［8］提出了利用植物叶片的边缘曲率来识别植物. MOKHTARIAN 等［9］利用多尺度曲率空间(CSS)方法识别遮掩的植物叶片. 树叶的长宽比及边缘曲率是树叶自动识别和分类的2个重要依据，因此本文将重点讨论这2个特征参数的提取.为了保证叶尖和叶片边缘的完整以及计算树叶边缘斜率与曲率的正确，需要在获取树叶长宽比及边缘曲率前将叶柄进行分离. 本文首先讨论利用数学形态学和像素跟踪相结合的算法实现叶片与叶柄的分离;然后利用霍特林变换计算树叶最小外接矩形及其长宽比;最后探讨叶片面积、边缘曲率及斜率的获取，这些特征参数的提取将为树叶的分类和识别奠定基础.

1 基本原理

1.1 二值化

首先将获得的RGB 图像转化为灰度图像，然后选取合适的阈值分离树叶和背景. 但由于不同种类的植物叶片在颜色和形状上存在差别，因此分离时阈值的设定不能为定值，要根据具体的树叶图像采用某一算法动态设定. 本文选用最大类间方差法(Otsu)［10］获取阈值. 其核心思想是:确定一个最佳阈值，使树叶和背景两个像素类的类间方差最大，从而达到分离树叶和背景的目的.具体算法为:对于灰度图像f(x，y)，设定某一灰度值t，利用该灰度值就可把图像的像素分成A 和B 两类，其中灰度值在［0，t］之间的像素组成A 类，灰度值在［t +1，255］之间的像素组成B 类，则A 类和B 类的类间方差D 为

其中w1和w2分别为A 类和B 类像素点占图像总像素点的比例，u1和u2分别为A 类和B 类像素点的平均灰度.依次在区域［0，255］内改变t 值，就可以得到一系列D 值.其中最大的D 值所对应的t 值就是最大类间方差的最佳阈值，利用该阈值就可分离树叶和背景.

由于树叶部分像素的灰度值与背景的灰度值很接近，在树叶和背景的分离过程中，将树叶像素点错判为背景，在图像中表现为树叶上有空洞.为了保证特征参数提取的准确性，需要对这些空洞进行填充.填充方法为:在图像中寻找值为1 的像素，判断其相邻行列是否有值为0 的像素，如果该像素的相邻区域均有值为0 的像素，则将该像素值改为0(背景的像素值为1，树叶的像素值为0).填充后的叶片图像如图1A 所示.

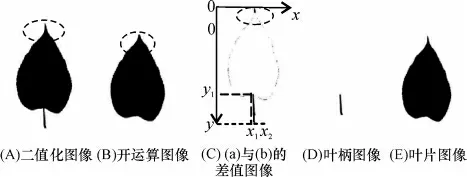
图1 分离叶柄Figure 1 Graphs of separating petiole

1.2 叶柄分离算法

用数学形态学算法［11－12］分离叶柄时，叶尖和叶片边缘的局部可能也被分离了，将影响特征参数的提取，本文采用数学形态学与像素跟踪相结合的算法分离叶柄.其中利用数学形态学粗略分离叶柄，然后用像素追踪法进行精细分离.

1.2.1 数学形态学 数学形态学分离叶柄的基础是腐蚀和膨胀.腐蚀主要使图像缩小，消除噪声，而膨胀使图像扩大，填补轮廓线的断裂，因此在分离叶柄时需要对图像进行膨胀、腐蚀处理. 其基本原理［13］为:

腐蚀时利用式(2)对图像进行操作

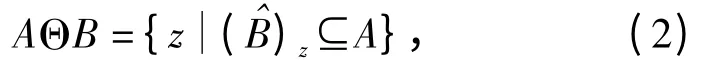
其中A 为图像像素，B 为结构元素，z 为位移.式(2)说明:在图像腐蚀时，先对B 做自身原点的映像，再将其映像平移z.若B 仍包含于A 中，则原点处对应的值为叶片像素.

膨胀时利用下式对图像进行操作

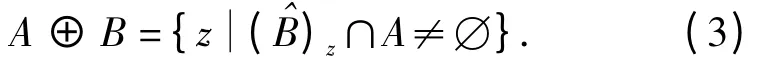
式(3)说明:若B 平移z 后与A 的交集不为空，则原点处对应的值为叶片像素.

本研究采用53 ×53 的方形结构元素，对图像进行一次腐蚀和膨胀运算，结果如图1B 所示，可看到:对二值图像做形态学运算，虽然达到了分离叶柄的目的，但叶尖和叶片边缘也有分离(图1C)，因此还需进一步处理.

1.2.2 像素追踪法 为保证叶尖和叶片边缘的完整性，用数学形态学法分离后还需用像素追踪法精细分离. 具体算法为:①将图1A 和图1B 相减得到图1C.图1C 中用虚线圈出的部分就是分离叶柄时被同时分离的叶尖部位. ②去掉图1C 中除叶柄之外的黑色像素点. 以图1C 的左上角为坐标原点建立坐标系，x 轴水平向右，y 轴水平向下.在坐标系中首先找到叶柄与叶片相连部位的坐标值y1以及叶柄宽度的坐标值x1和x2，然后将其余部分的黑色像素变为白色像素，这样就可以准确得到叶柄的图像，如图1D 所示.③将图1A 和图1D 做差值运算可得到分离叶柄后树叶的图像，如图1E 所示.

1.3 获取长宽比的算法

在获取树叶长宽比和边缘曲率等轮廓特征时，首先需要获取树叶的边缘坐标. 本文选用bwboundaries 函数获得树叶的边缘和边缘像素的坐标值.在得到树叶的边缘及坐标后，利用霍特林变换获取树叶的最小外接矩形，进而得到树叶的长宽比.

霍特林变换［14］是建立在统计特征基础上的一种变换，该变换通过线性变换找到一组最优的单位正交基向量，用该组基向量的线性组合来重新表示原样本.具体算法为:设树叶图像边缘像素点的个数为k，把树叶的每个边缘坐标点作为一个二维向量Xi=［ai，bi］T(i =1，2，…，k). 根据所有Xi计算树叶边缘坐标的均值向量mx和协方差矩阵cx

由于cx是2 ×2 阶对称矩阵，故特征向量只有2个.这2个特征向量组成的矩阵可表示为A =(e1，e2)T，其中e1为最大特征值对应的特征向量，e2为最小特征值对应的特征向量.利用A 作运算即可得到一组新的向量:

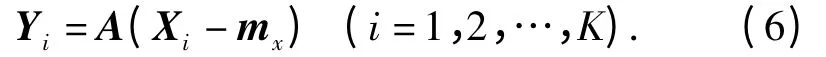
由此建立一个新的坐标系:以树叶质心(均值向量mx)为原点，以e1作为新坐标横轴的方向，e2作为新坐标纵轴的方向. 坐标旋转变换后即可得到树叶最小外接矩形的长宽比:

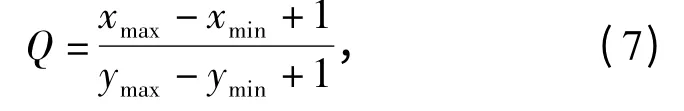
其中xmax和xmin分别是树叶轮廓横坐标的最大值和最小值;ymax和ymin分别是树叶轮廓纵坐标的最大值和最小值.

1.4 边缘曲率的算法

采用有限差分算法计算树叶的边缘曲率［15］.对于树叶边缘c(t)=［x(t)，y(t)］，曲率函数K(t)可写为:

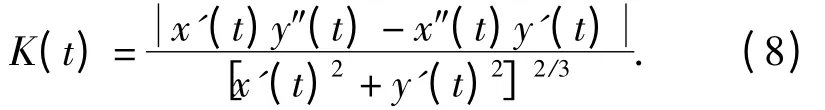
将x(t)和y(t)离散后，进行有限差分:

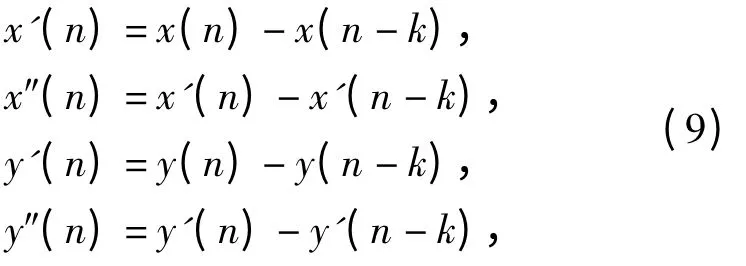
其中k 为步长(本文设为10)，将式(9)代入式(8)即可得到曲率K.

2 结果与分析

选取2 种不同形态的树叶，利用上面所提到的算法获取2 片树叶的长宽比、面积、边缘曲率和斜率.

2.1 长宽比和面积

2 片树叶的边缘追踪结果如图2A、C 中的白线所示，经霍特林变换后的图像及其外接矩形图像如图2B、D 所示.

树叶1 和树叶2 的最小外接矩形长宽比分别为1.32∶1 和1.30∶1，而树叶1 的面积为55.794 3 cm2(树叶RGB 图像的分辨率为600 dpi)，树叶2 的面积为192.71 cm2(树叶RGB 图像的分辨率为96 dpi).

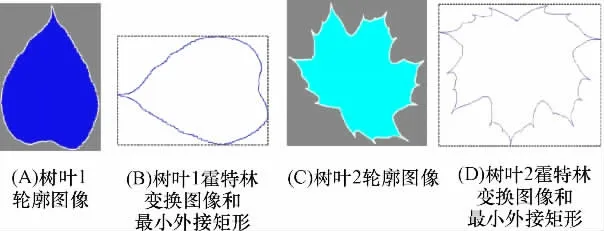
图2 树叶边缘的霍特林变换图像及其最小外接矩形Figure 2 Graphs of the Hotelling transform and minimum enclosing rectangle

2.2 边缘曲率和斜率变化趋势

树叶的边缘斜率反映了叶片边缘变化的快慢程度，而曲率反映了叶片边缘曲线的弯曲程度，这2个参数在一定程度上反映了叶片的轮廓特征. 叶片边缘斜率可通过边缘点附近的y 轴坐标差值Δy 与相应的x 轴坐标差值Δx 的比值来求得.本文选取了边缘呈锯齿状的叶片1 和枫叶2 作为示例树叶，其边缘曲线分别如图3A 和图4A 所示(步长为10). 图3B 和图4B 为2 片树叶的边缘斜率. 为了更清楚地说明斜率的正负，在图3B 和图4B 中设定了斜率为0 的边缘曲线，用粗线所示.图3C 和图4C 是2 片树叶的边缘曲率. 从图3、图4 可以看出:①若叶片边缘锯齿状的分布越多且变化越剧烈，相应的边缘斜率和曲率的波动也越剧烈，如图3A、B 虚线圈出的部分.②边缘曲率突变的地方表示叶片边缘在该部位有大的弯曲. 图4C 中圈出部分曲率的极大值反映了图4A的圈出部分的弯曲程度.以上结果表明树叶边缘的斜率和曲率也是树叶的重要参数.

图3 锯齿形叶片的斜率和曲率Figure 3 The slope and curvature of sawtooth edge leaf

图4 枫叶的斜率和曲率Figure 4 The slope and curvature of maple leaf

为了保证叶尖和叶片边缘的完整性，本文采用数学形态学法与像素追踪法相结合对叶柄进行分离，与传统算法比较，这2 种算法的结合使得叶柄分离更为精细.在此基础上运用霍特林变换获得了叶片的长宽比，该算法具有算法简单和运算速度快的优点，同时运用有限差分算法得到了体现树叶重要特征的边缘斜率和曲率.

3 结论

采用数学形态学和像素追踪相结合的算法分离叶柄，并选取了2 种不同形状的树叶，在分离叶柄后运用霍特林变换和有限差分算法得到了这2 种树叶的轮廓特征. 结果表明:本文采用的叶柄分离算法可以准确地分离叶柄并获得不同形状树叶的边缘斜率和曲率，这些算法对下一步进行树叶的自动识别和树叶档案数据库的建立具有重要的意义.

［1］王小铭.计算机图像图形学应用研究的现状与发展策略刍议［J］. 华南师范大学学报:自然科学版，1998(4):108－111.

［2］ZHENG X D，WANG X J.Fast leaf vein extraction using hue and intensity information［C］∥Proceedings of IEEE International Conference on Information Engineering and Computer Society，2009:1－4.

［3］李灿灿，孙长辉，王静，等.基于改进的Sobel 算子和色调信息的叶脉提取方法［J］.农机工程学报，2011(7):196－199.

［4］JOAO C，GEORGE M，DAVID D J，et al.Plant species identification using Elliptic Fourier leaf shape analysis［J］.Comput Electron Agr，2006(50):121－134.

［5］王晓峰，黄德双，杜吉祥，等. 叶片图像特征提取与识别技术的研究［J］. 计算机工程与应用，2006(3):190－193.

［6］李宝光，黄芳.植物叶片面积的测定方法［J］.山东理工大学学报，2004，18(4):94－96.

［7］王忠芝，张金瑞. 基于图像处理的叶面积测量方法［J］.微计算机应用，2010，31(5):68－72.

［8］FRANZ E，GEBHARDT M R，UNKLESBAY K B，et al.Shape description of completely visible and partially occluded leaves for identifying plants in digital images［J］.Transactions of the ASAE，1991，34(2):673－681.

［9］MOKHTARIAN F，ABBASI S.Matching shape with selfintersection application to leaf classification ［J］. IEEE Trans on Image Processing，2004，13(5):653－661.

［10］OTSU N. A threshold selection method from gray－level histogram［J］. IEEE Trans Actions on SMC，1979(9):652－655.

［11］郑小东，王晓洁，赵中堂. 基于形状特征的植物叶柄与叶片分割算法［J］. 计算机工程与设计，2010，31(4):918－922.

［12］王晓洁，郑小东，赵中堂. 基于数学形态学的植物叶柄与叶片分割［J］.农机化研究，2009(8):42－44.

［13］RAFAEL C G，RICHARD E W. 数字图像处理［M］.2版.阮秋琦，阮宇智，等译. 北京:电子工业出版社，2007:235－237.

［14］刘璎瑛，丁为民，陈建伟，等.基于霍特林变换的稻米彩色图像粒形检测算法［J］.中国水稻科学，2010，24(3):325－328.

［15］马旭，杨文关.医疗特征图像边缘曲率分析实例［J］.医学影像学杂志，2010，20(11):1713－1715.