基于达朗贝尔解法的一维有界弦振动方程的求解

叶 松 王向贤 余建立

（巢湖学院电子工程与电气自动化学院，安徽 巢湖 238000）

弦振动方程有重要的工程应用价值。求解一维弦振动方程得到斜拉桥钢索的应力与固有频率的函数关系，对评估斜拉桥梁承载能力和安全系数是有利的；基于弦振动方程建立弦线密度与固有频率的函数关系，可以应用到弦线密度测量[1-4]。描述固有频率与各物理量关系的理想化方程是弦振动方程。

无界弦振动方程的达朗贝尔解法的物理思想是将弦振动视作一定初值条件下的两列行波的叠加。达朗贝尔解法是应用物理思想指导在数学物理方程求解的典型案例。但是对有界弦振动方程，目前国内流行的相关教材均采用分离变量法求解，其解表示不同频率简谐波的叠加。物理上，联系达朗贝尔解法和分离变量法的纽带是波的叠加原理。因此利用达朗贝尔解法的物理思想推导出弦振动方程的解是可行的。而目前使用较为广泛的几本数学物理方法的教材均没有对该方法的论述[5，6]。本文基于达朗贝尔解法的基本思想，分析狄利克雷边界条件和诺依曼边界条件时的弦振动方程解的特征，得到弦振动方程的傅立叶级数解。本文的解法拓宽了达朗贝尔解法的应用，对加深分离变量解法的理解有一定的意义，一定程度上丰富了工程数学的教学内容。

1 两端固定的有界弦振动方程达朗贝尔解法

两端固定的有界弦振动方程为：

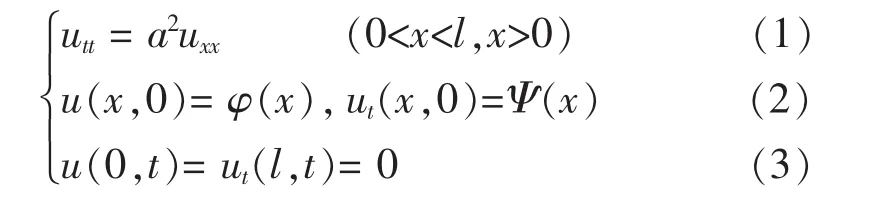
考虑泛定方程行波形式的通解：

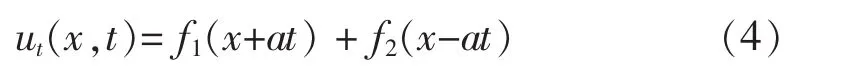
为得到满足定解条件的解的表达式，应用边界条件（2）：

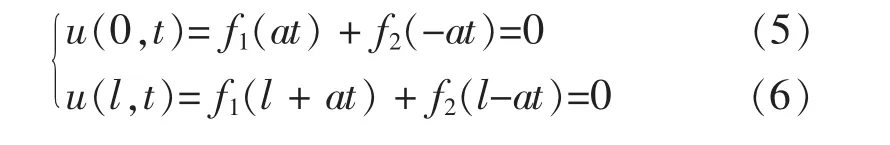
（5）和（6）式等价于：

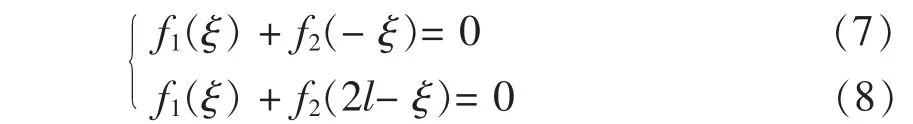
或

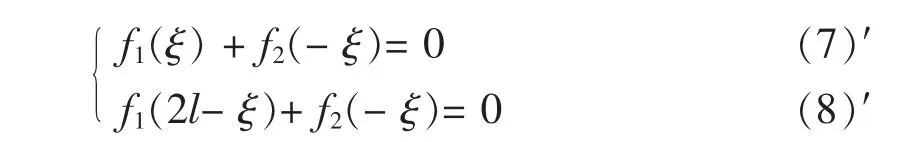
因此，狄利克雷边界条件的解是以2l为周期的函数：

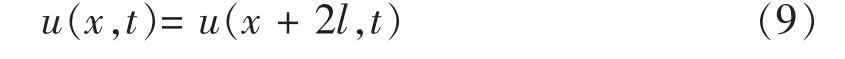
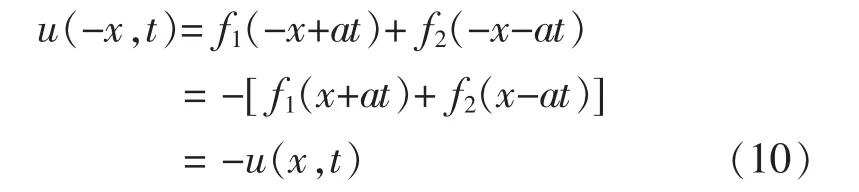
所以，u（x，t）是 x 自变量以 2l为周期的奇函数。因此u（x，t）可以用傅立叶级数表示：

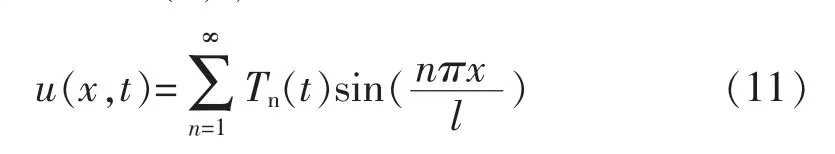
将（11）式带入（1）式，得到：

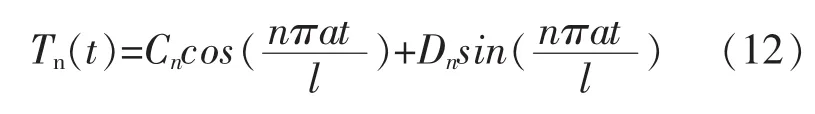
因此方程（1-3）的解为：

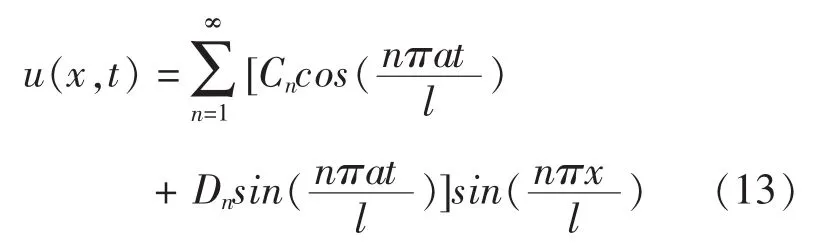
其中：

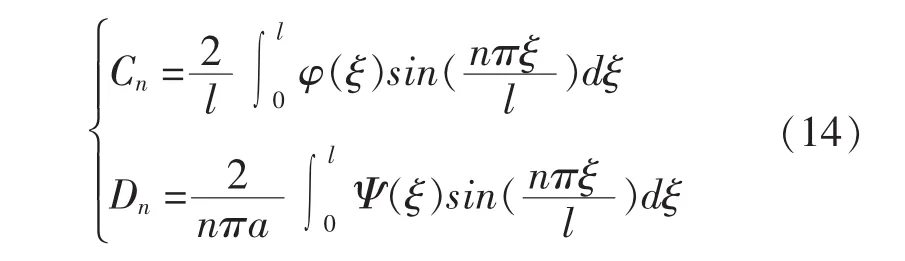
2 两端自由的有界弦振动方程达朗贝尔解法

两端自由的有界弦振动方程为：

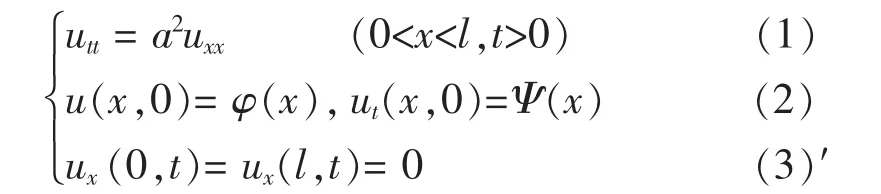
与两端固定的弦振动的分析相似，并注意到周期函数的一阶导数是同周期的函数和奇 （偶）函数的一阶导数是偶（奇）函数，可以证明：

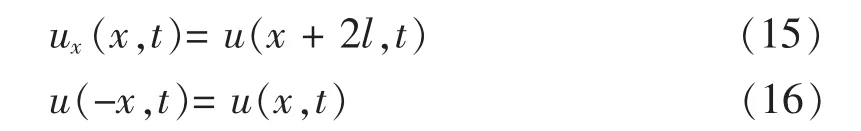
因此 u（x，t）可以用傅立叶级数表示：

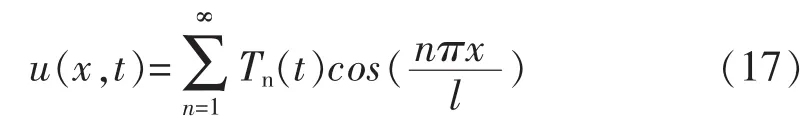
同上讨论，解的形式为：

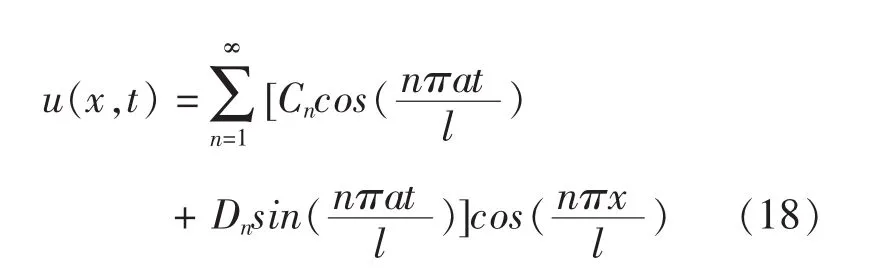
其中：

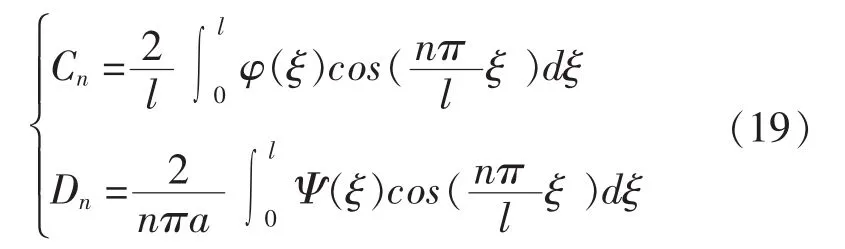
3 一端自由一端固定的有界弦振动方程达朗贝尔解法

一端自由一端固定的有界弦振动方程为：

设方程（1）的解为：

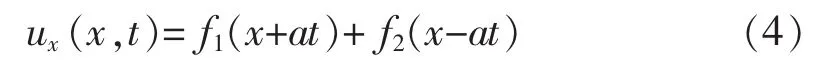
其对x的一阶偏导数为：

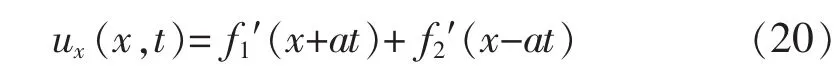
由方程 （3）″得：

（21）和（22）式等价于：

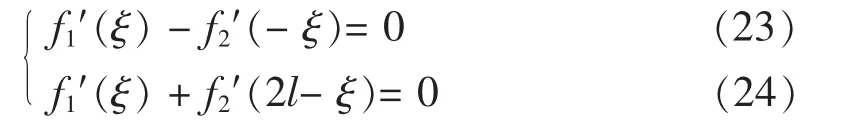
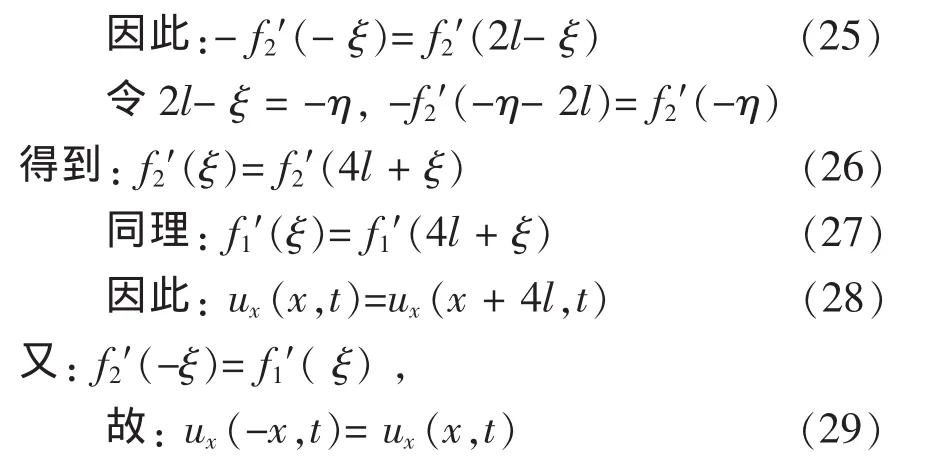
（28-29）式说明 ux（x，t）是 x 自变量的周期偶函数，其傅立叶级数形式为：

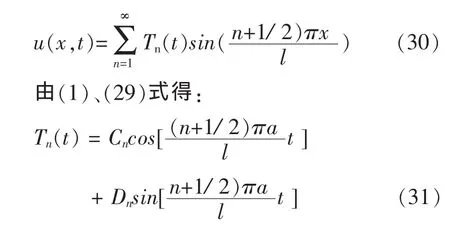
因此，方程的解为：

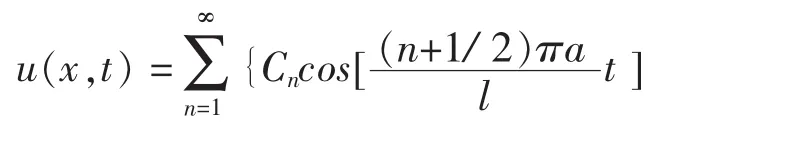
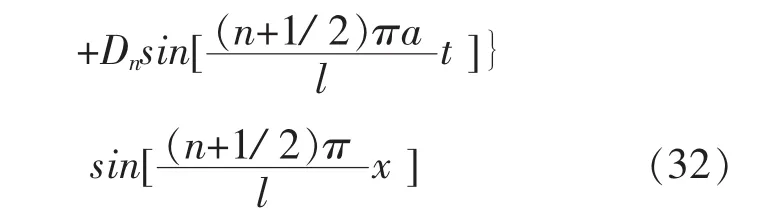
其中：

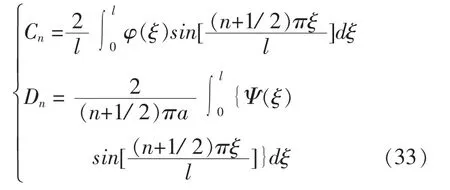
4 结论

本文运用达朗贝尔解法的物理思想得到了在工程中有实际意义的三种边界条件下的弦振动方程的解。本文的解法拓宽了达朗贝尔解法的应用，对理解分离变量解法有一定的帮助，丰富了工程数学的教学内容。

[1]陈丕华，王修勇，陈政清，等.斜拉索面内参数振动的理论和试验研究[J].振动与冲击，2010，29（2）：50-53.

[2]方志，汪建群，颜江平.基于频率法的拉索及吊杆张力测试[J].振动与冲击，2007，26（9）：78-82.

[3]来侃，姚穆.激振式纤维线密度测试中影响参数的研究[J].西北纺织工学院学报，2001，15（2）：253-256.

[4]林有勤.利用振动法测量预应力体外索的索力[J].地震工程与工程振动，2007，27（3）：64-69.

[5]梁昆淼.数学物理方法[M].北京：高等教育出版社（第四版），2010.

[6]吴崇试.数学物理方法[M].北京：北京大学出版社（第二版），1999.