非双倍测度上的θ-型Caldero′n-Zygmund算子

王海莲 王良龙 郝江锋

（1 安徽大学数学科学学院，安徽 合肥 230039）

（2 巢湖学院数学系，安徽 巢湖 238000）

1 引言及主要结果

在过去的一段时间里，非双倍测度上的奇异积分算子的有界性被广泛地研究，参考文献[1-7].设μ是Rd上的非双倍Radon测度，对所有的x∈Rd，r＞0和某些固定的0＜n≤d，满足

其中C是与x和r无关的正数.对于x∈supp μ和 r＞0，若存在正常数C使得μ（B（x，2r））≤C μ（B（x，r）），则称 μ 满足双倍条件。

令θ是一个定义在R+=（0，∞）上的非负不减函数，满足

关于上述核和测度μ的θ-型Calder ο′n-Zygmund算子被定义为

这个积分可能对许多函数都不收敛，从而考虑截断函数Tε（ε＞0），其定义为

若 Tε关于 ε＞0 在 LP（ μ）上一致有界，则称 T 在 LP（ μ）上有界.

Tolsa在[1]中建立了非双倍测度上的Calder ο′n-Zygmund理论。后来，胡国恩、孟岩和杨大春等在[2-4]中研究了非双倍测度上的奇异积分的极大算子和多线性交换子。受这些文献的启发，本文研究了θ-型 Calder ο′n-Zygmund 算子若满足 L2（ μ）有界性，则是从 L∞（ μ）到 RBMO（μ）上有界算子。在给出主要结果之前，先回顾一些定义。

设Rd中的方体Q是一个闭方体，其边平行于坐标轴且边长记为l（Q）。令a和βd是满足a＞1和βd＞an的正常数。若 μ（aQ）≤β μ（Q），则称 Q 是（a，β）双倍方体，其中 aQ 表示以 Q 的中心为中心，边长为al（Q）的方体。对于两个方体Q⊂R，令

其中NQ，R表示满足 l（2kQ）≥l（R）的最小正整数 k.

定义1[1]设b是μ-局部可积函数，称b∈RBMO（μ）.如果存在一个常数C＞0使得

且对于任何两个双倍方体Q⊂R，有

满足（7）和（8）的最小常数 C 称为 b 的 RBMO（μ）范数，记为‖b‖*.

Tolsa在[1]中说明了RBMO（μ）的定义与 ρ，α＞1和 βd＞αn的选取无关。本文我们选取 ρ＝ α ＝2和βd＞2d+1.若 Tε关于 ε 从 L∞（ μ）到 RBMO（μ）上一致有界，则称 T 从 L∞（ μ）到 RBMO（μ）上有界。

定理 1 若 θ-型 Calder′on-Zygmund 算子 T 是 L2（ μ）有界的，则它是从 L∞（ μ）到 RBMO（μ）上的有界算子。

注 全文中的C是一个与主要参数无关的正常数，但是它在不同的地方有可能取的值不同。用p′表示p的共轭指数，即满足

2 定理的证明

为了证明定理1，我们利用[1]中RBMO（μ）的等价定义。

引理 1 设f∈Lloc（μ），下面两个命题是等价的：

（b）存在一个常数C＞0使得对每个方体Q，

且对于任何两个双倍方体Q⊂R，

定理 1 的证明 首先证明若 f∈L∞（ μ）∩LP0（ μ），P0∈[1，∞），则

对于任何方体Q，

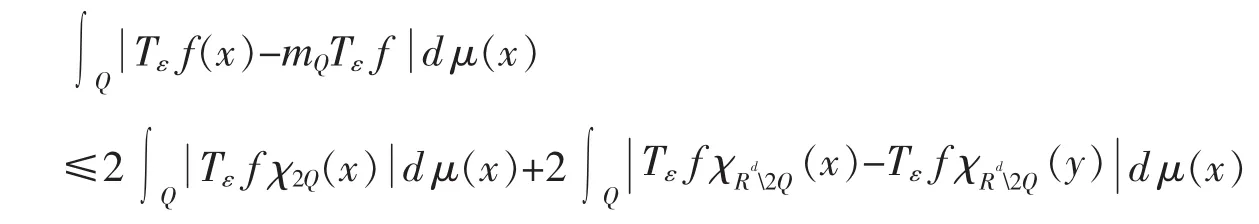
由 Ho¨lder不等式和 T 的 L2（ μ）有界性，得到

通过条件（4），对任何 x，y∈Q，有

这里我们使用了下面的不等式：

因此

接下来证明（10）成立，即证明若Q⊂R，则有

因为NQ，R表示满足 2kQ⊃R 的最小正整数k.令QR=2NQ，R+1Q，对于 x∈Q和 y∈R，有

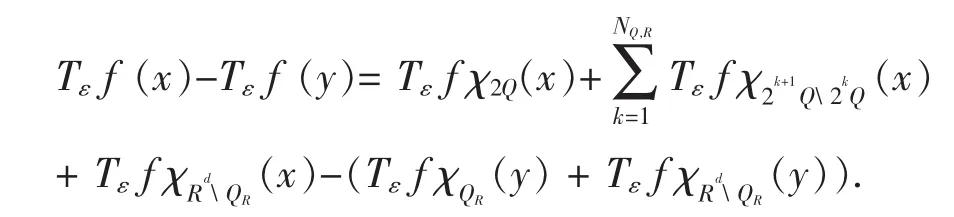
因为

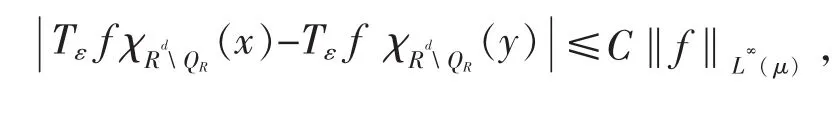
所以现在对x在Q上取平均，对y在R上取平均，由T的L∞（μ）有界性，得到

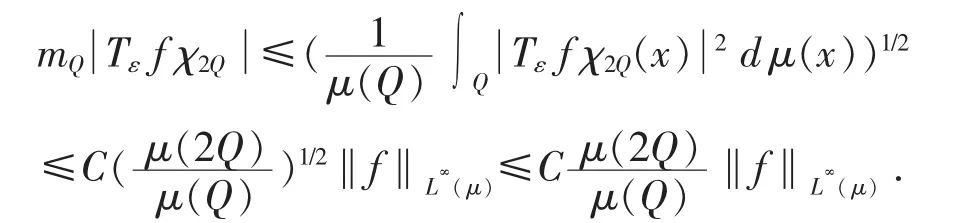
另一方面，因为l（QR）≈l（R）得到

从而

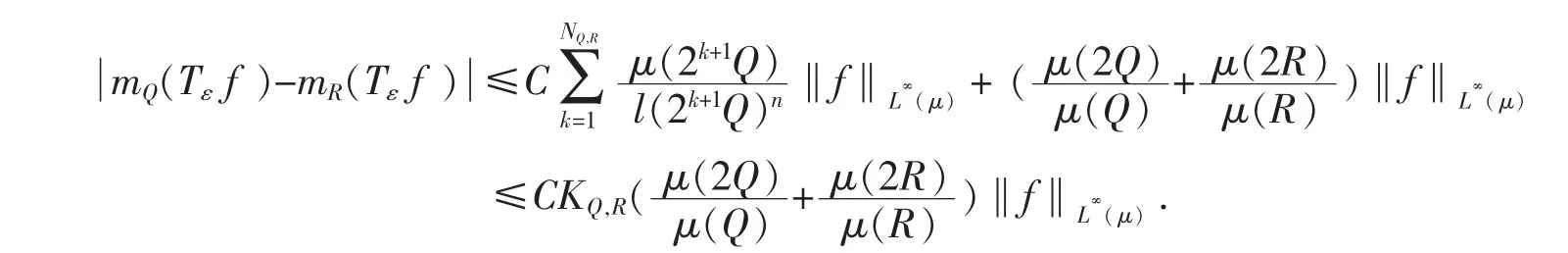
[1]Tolsa X.and Calder′on-Zygmund operators for non doubling measures[J].Math.Ann.,2001，19：89-149.

[2]Hu G,Meng Y,Yang D.Multilinear commutators of singular integrals with non doubling measures[J].Integr.equ.oper.theory,2005，51：235-255.

[3]Hu G,Meng Y,Yang D.Estimates for maximal singular integral operators in non-homogeneous spaces[J].Proc.Roy.Soc.Edinburgh,2006，136A：351-364.

[4]Meng Y,Yang D.Multilinear commutators of Calder′on-Zygmund operators on Hardy-type spaces with non-doubling measures[J].J.Math.Anal.Appl.,2006，317：228-244.

[5]Fu X,Meng Y,Yang D.Boundedness of commutators with Lipschitz functions in non-homogeneous spaces[J].Chin.Ann.Math.,2007，28B：67-80.

[6]Tolsa X.Littlewood-Paley theory and the T （1） theorem with non-doubling measures[J].Adv.Math.,2001，164：57-116.

[7]Tolsa X.The space H1 for nondoubling measures in terms of a grand maximal operator[J].Trans.Amer.Math.Soc.,2003，355：315-348.