二层信用支付下非瞬间变质的供应链库存模型

郝家芹 陈攀峰 姚云飞

（1 宿州学院数学与统计学院，安徽 宿州 234000）（2 阜阳师范学院数学与计算科学学院，安徽 阜阳 236032）

1 引言

经典的供应链库存模型大多数假设零售商在收到订购的物品时支付全部货款，但现实销售过程中供应商为了提高市场销售额，常允许零售商延期一段时间支付货款，延期时间称为信用期。同样，零售商为了刺激消费，也常提供给其顾客一定的信用期。本文将零售商在享有供应商提供信用期的同时也提供给其顾客信用期的销售策略定义为二层信用支付策略。2003年，Huang首次将二层信用支付策略引入EOQ模型[1]。此后，Liao和Chang等研究了二层信用支付下变质物品的最优订货问题[2]-[3]；Mahata分析了二层信用支付下部分延期付款且考虑易变质物品的经济生产批量的库存问题[4]；闵杰等在二层信用支付的前提下研究了线性时变需求的供应链库存问题[5]；潘义前等构建了需求是时间指数函数的二层信用支付的变质物品的库存模型[6]。这些文献均未考虑货币时间价值对库存系统的影响。

然而，库存存在资金投入和公司资产有限下的投资竞争问题并且货币在不同的时间常常具有不同的价值。因此，在库存控制策略中考虑时间对货币价值的影响是十分必要的。Chang等用贴现现金流的方法研究了信用期依赖订购量的变质物品的库存控制问题，其文中假设若顾客的订购量超过预先设定的订购量，供应商提供给其两种购买方案，即延长信用期和价格折扣[7]；Chung等利用货币折现的方法分析了信用支付下变质物品的最优订购问题[8]；Chung等采用贴现现金流的方法讨论了零售商的信用期依赖订购量的库存问题，其文中假设若顾客的订购量小于预先设定的订购量，顾客需立即支付货款，否则供应商提供给其信用期[9]；Liao等在考虑货币时间价值的前提下建立了二层信用支付下的变质物品的EOQ模型[10]。

上述关于变质物品的文献均假设物品进入库存系统立即发生变质，但在现实经济生产中物品有一定保质期，保质期过后才会发生变质，例蔬菜、水果等。为了使库存模型更贴近现实，本文研究了二层信用支付下的库存问题，假设供应链中流通的物品具有一定的保质期并且考虑时间对货币价值的影响，讨论了模型最优解的存在性和唯一性。最后用数值例子对模型的理论结果进行了验证，对主要参数做了灵敏度分析。

1 模型的符号说明与假设

（1）A、c、p、h分别表示每次的订购费、单位物品的购买成本、单位售价以及单位物品单位时间的存储费（不含利息支出）；r、D、Q分别为连续的折现率、单位时间的需求量以及每次订购量；T为一个订货周期（决策变量）；PV∞（T）表示整个计划期内零售商的相关成本的贴现值；

（2）瞬间供货，不允许缺货；提前期为零；计划期长度无限；多次订货且每次订货周期的时间长度相等；

（3）物品的保质期为 Tθ，当 0＜T≤Tθ时不发生变质；当 T ＞ Tθ时以常数 θ（0＜θ＜1）的速率发生变质，物品一旦变质立即离开库存系统且残值为零；

（4）供应商提供给其信用期M：在信用期内，零售商无需向供应商支付任何费用，其销售收入可以获得以Ie为年收益利率的利息；在信用期的最后时刻支付所有购买成本；之后，若库存有剩余，零售商开始支付库存成本产生的以Ip为年支付利率的利息；

（5）零售商提供给顾客信用期N：顾客在时刻N前订购物品，需在N时刻付清货款，N时刻之后购买的物品需立即支付货款，并假设：0≤N≤M；

（6）I（t）为 t∈（0，T]内 t时刻的库存水平；当 T ＞ Tθ时，I（t）记为（0，Tθ]内 t时刻的库存水平；I2（t）记为（Tθ，T]内 t时刻的库存水平；

（7）为简化模型，假设 rce-rm+h-pIe（e-rN-e-rM）≥0.

2 模型的建立

由假设知，在每个供货周期开始时有Q个单位的物品进入库存系统。当0≤T≤Tθ时，库存物品由于需求而减少，在T时刻下降为零。因此，t时刻的库存水平I（t）的变化可以表示为

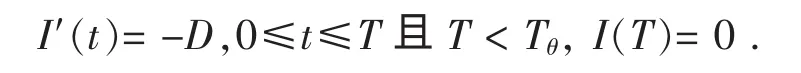
解上述微分方程，得 I（t）=D（T-t）， 0≤t≤T 且 T ＜ Tθ.

此情形下，每次的订购量Q为Q=I（0）=DT.

当T＞Tθ时，库存水平的变化分为两个阶段：在（0，T]内，库存水平由于需求而减少，此时库存水平I1（t）可以表示为 I1′（t）=-D， 0≤t≤Tθ， I1（0）=Q.

解上述微分方程，得

在（Tθ，T]内库存物品由于需求和变质使得库存水平下降，并且在T时刻库存水平下降为零。因此，在（Tθ，T]内 t时刻库存水平 I2（t）的变化可以表示为 I2′（t）=-D-θI2（t），Tθ≤ t≤ T， I2（t） =0.

解上述微分方程，得

由于在 t=Tθ时刻，库存物品是连续变化的，因此有 I1（Tθ）=I2（Tθ），所以

将（3）式带入（1）式得 I1（t）的解析式：I1（T）=D（Tθ-t）+D[eθ（T-Tθ）-1]/θ，0≤t≤Tθ.

整个无限计划期内，零售商的相关成本的贴现值由以下几个部分组成。

（1）订购费的贴现值 V0=A/（1-e-rT）；

（2）库存维持费的贴现值

当 0＜T≤Tθ时

当T＞Tθ时，

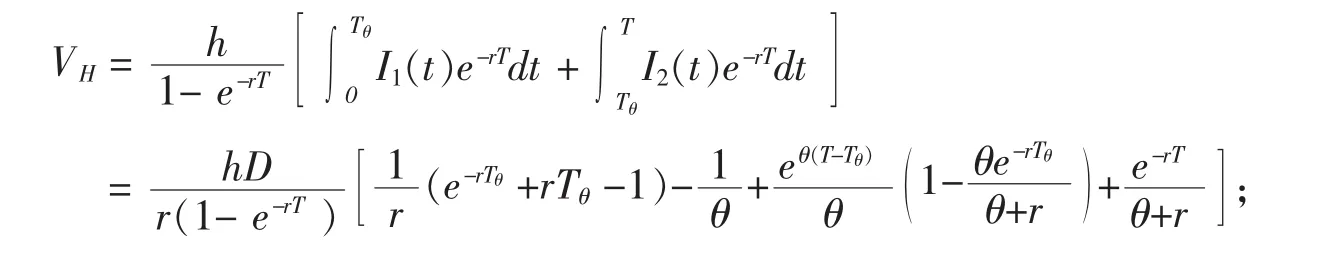
（3）购买成本的贴现值

（4）零售商的利息支出的贴现值VIP

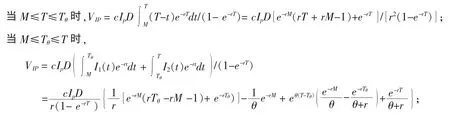
当 Tθ≤M≤T时，

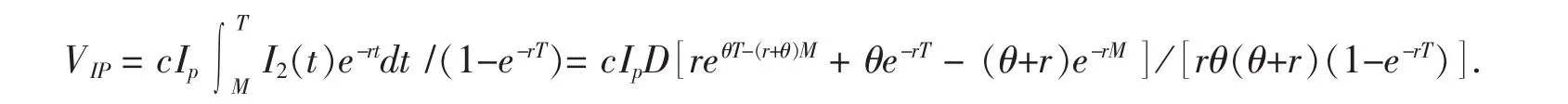
（5）零售商的利息收入的贴现值

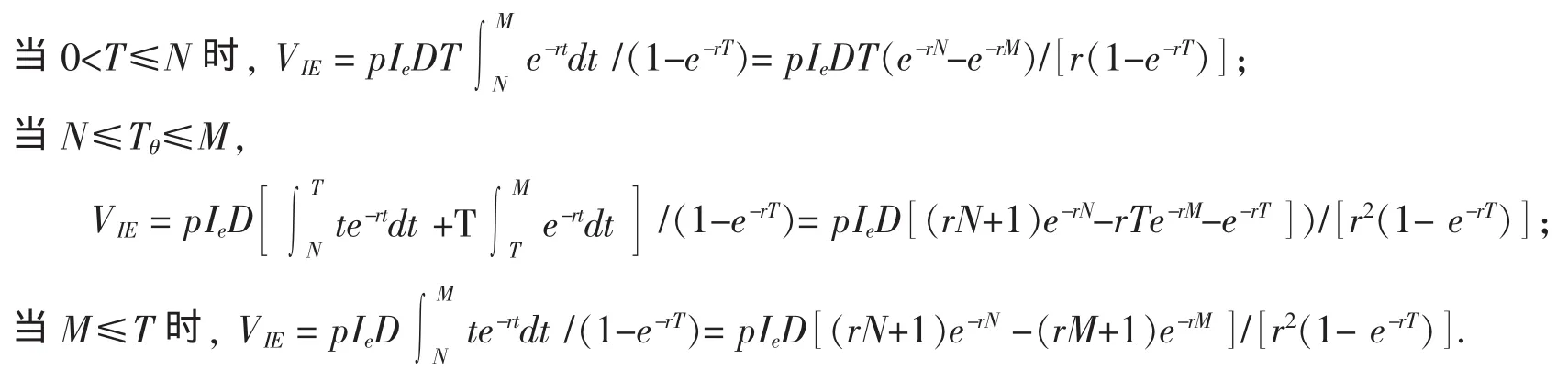
整个无限计划内，零售商的相关成本的贴现值PV∞（T）为

本文的目标函数分以下三种情形：0＜Tθ≤N；N＜Tθ≤M；M≤Tθ.

当 0＜Tθ≤N 时，PV∞（T）为

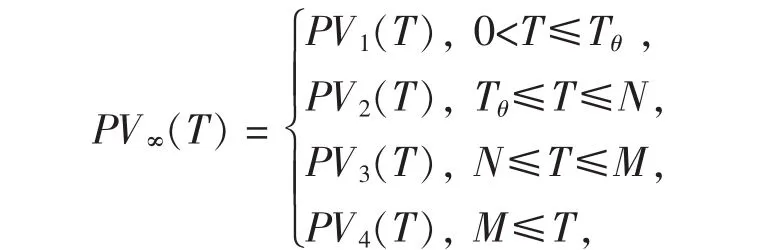
其中

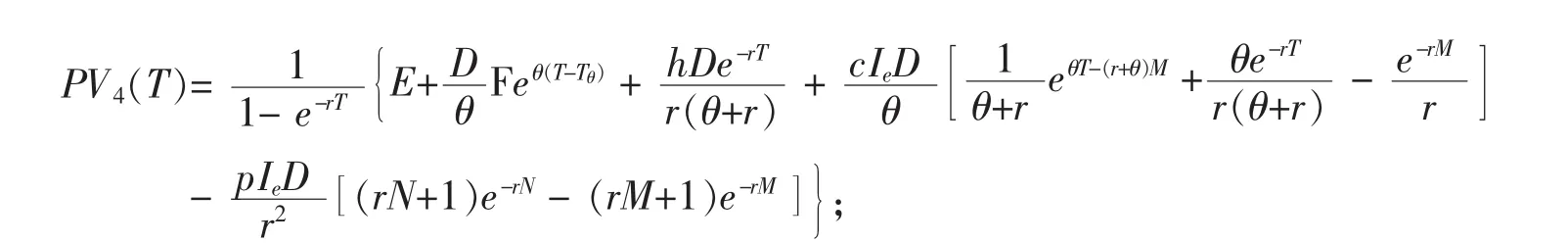
由 PV1（Tθ）=PV2（Tθ）、PV2（N）=PV3（N）和 PV3（M）=PV4（M）知，PV∞（T）在（0，+∞）内是连续函数。

当 N≤Tθ≤M 时，PV∞（T）为

由 PV1（N）=PV5（N）、PV5（Tθ）=PV3（Tθ）和 PV3（M）=PV4（M）知，PV∞（T）在（0，+∞）内是连续函数。

当 M≤Tθ时，PV∞（T）为

由 PV1（N）=PV5（N）、PV5（M）=PV6（M）和 PV6（Tθ）=PV7（Tθ）知，PV∞（T）在（0，+∞）内是连续函数。

3 理论结果

引理 1 设 F（x）=f（x）e-rx/（1-e-rx）2，其中 f（x）为区间[a，b]上连续增函数，x*为 F（x）在区间[a，b]上的最小值点。

（1）若 f（a）≥0，则 F（x）在[a，b]内是增函数；（2）若 f（a）＜ 0＜ f（b），则 F（x）在[a，x0]内是减函数，在（x0，b]内是增函数，其中 x0为 f（x）=0 在（a，b）内的唯一解；（3）若 f（b）≤0，则 F（x）在[a，b]内是减函数。

定理 1 当 0 ＜ Tθ≤N 时，设 T*为 PV∞（T）在（0，+∞）内的最小值点，则

（1）当 f2（Tθ）≥0、 f3（N）≥0、f4（M）≥0 时，其中为 f1（T）=0 在（0，Tθ）内的唯一解；

（2）当 f2（Tθ）＜0、 f3（N）≥0、 f4（M）≥0 时，其中在（Tθ，N）内的唯一解；

（3）当 f2（Tθ）＜0、 f3（N）＜0、 f4（M）≥0 时，，其中为 f3（T）=0 在（N，M）内的唯一解；

（4）当 f2（Tθ）＜0、 f3（N）＜0、 f4（M）＜0 时，，其中为 f4（T）=0 在内（M，+∞）的唯一解。

证明：PVi（T）（i=1，2，3，4）关于 T 的一阶导数，得

其中

并且 f1（0） =-rA 且

由 PV1（Tθ）=PV2（Tθ），PV2（N）=PV3（N）和 PV3（M）=PV4（M）得

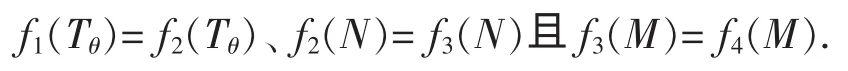
下面 fi（T）（i=1，2，3，4）关于 T 求一阶导数，得

定理 1（1）的证明：

由假设（6）可知 fi′（T）≥0（i=1，2，3，4），再由引理 1 可得：

（1）当 T≤Tθ时，若 f1（Tθ）≤0，则 PV1（T）在（0，Tθ]在内是减函数；否则，PV1（T）在内是减函数，在内是增函数，其中在（0，Tθ]内的唯一解；

（2）当 Tθ≤T≤N 时，（a）若 f2（Tθ）≥0，则 PV2（T）在[Tθ，N]内是增函数；（b）若 f2（Tθ）＜ 0 ＜ f2（N），则PV2（T）在内是减函数，在内是增函数，其中内的唯一解；（c）若f2（N）≤0，则 PV2（T）在[Tθ，N]内是减函数；

（3）当 N≤T≤M 时，（a）若 f3（N）≥0，则 PV3（T）在[N ，M]内是增函数；（b）若 f3（N）＜ 0 ＜ f3（M），则PV3（T）在内是减函数，在内是增函数，其中为 f3（T）=0 在（N ，M）内的唯一解；（c）若f3（M）≤0，则 PV3（T）在[N ，M]内是减函数；

（4）当 M≤T 时，若 f4（M）≥0，则 PV4（T）在[M ，+∞]内是增函数；否则，PV4（T）在内是减函数，在内是增函数，其中在（M，+∞）内的唯一解。

再由 PV1（Tθ）=PV2（Tθ）、PV2（N）=PV3（N）、PV3（M）=PV4（M）、 f1（Tθ）=f2（Tθ）、 f2（N）=f3（N）以及 f3（M）=f4（M）可得：当 f2（Tθ）≥0、 f3（N）≥0、f4（M）≥0 时，PV（T）在区间内是减函数，在区间内为增函数，故而

定理 1（2）、（3）、（4）同理可得证。

定理 2 当 N≤Tθ≤M 时，设 T*为 PV∞（T）在（0，+∞）内的最小值点，则

（1）当 f5（N）≥0、 f3（Tθ）≥0、 f4（M）≥0 时，，其中在（0，N）内的唯一解；

（2）当 f5（N）＜0、 f3（Tθ）≥0、 f4（M）≥0 时，其中在（N，Tθ）内的唯一解；

证明：PV5（T）关于 T 的一阶导数，得

其中

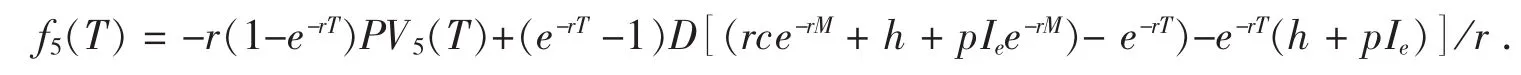
由 PV1（N）=PV5（N）、PV5（Tθ）=PV3（Tθ）和 PV3（M）=PV4（M）得下面f5（T）关于T求一阶导数，得

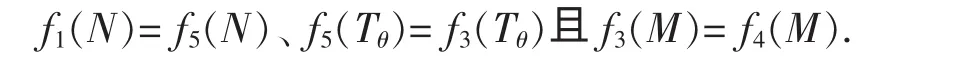
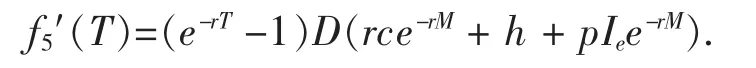
与定理1的证明过程类似，定理2可得证。

定理 3 当 M ＜ Tθ时，设 T*为 PV∞（T）在（0，+∞）内的最小值点，则

（1）当 f5（N）≥0、 f6（M）≥0、 f7（Tθ）≥0 时，

（2）当 f5（N）＜0、 f6（M）≥0、 f7（Tθ）≥0 时，，其中在（N，M）内的唯一解；

（3）当 f5（N）＜0、 f6（M）＜0、 f7（Tθ）≥0 时，，其中为 f6（T）=0 在（M，Tθ）内的唯一解；

（4）当 f5（N）＜0、 f6（M）＜0、 f7（Tθ）＜0 时，，其中为 f7（T）=0 在（Tθ，+∞）内的唯一解。

证明：PVi（T）（i=6，7）关于 T 的一阶导数，得

其中

由 PV1（N）=PV5（N）、 PV5（M）=PV6（M）和 PV6（Tθ）=PV7（Tθ）得

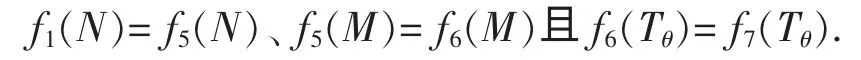
下面 fi（T）（i=6，7）关于 T 求一阶导数，得与定理1的证明过程类似，定理3可得证。

4 数值例子

用下面的数值例子说明本模型的可行性。

令 A=350；c=15；p=17；Ip=0.15；Ie=0.1；h=0.5；θ=0.08；D=1000；M=0.5；N=0.3；r=0.08；Tθ=0.2.

例 当 Tθ=0.4 时，（1）若 A=10，则 f1（N）=5.1029、 f5（Tθ）=14.4354、 f3（M）=30.8098，由定理 2（1）知：；（2）若 A=100，则 f1（N）=-2.0971 f5（Tθ）=7.2354、f3（M）=23.6098，由定理 2（2）知：（3）若 A=350，则，由定理 2（3）知，（4）若 A=1000，则 f1（N）=-74.0971、 f5（Tθ）=-64.7646、 f3（M）=-48.3902，由定理 2（4）知：

下面分析当Tθ=0.4时M、N的变化对零售商的最优订货周期及其相关成本的最小值的影响。

M N PV∞（T*） T*0.40 186640 0.4759 0.5 0.30 191040 0.4798 0.35 191750 0.4920 0.40 192540 0.5049 0.6 0.30 187510 0.4812 0.35 188210 0.4934 0.40 189000 0.5070 0.7 0.30 184000 0.4825 0.35 184700 0.4947 0.40 185490 0.5084

由上表可知：

（1）当其他参数保持不变时，最优解和最优值均随着信用期N的增大而增大；

（2）当其他参数保持不变时，最优解随着M的增大而增大，而最优值随着M的增大而减小。

下图是折现率对零售商的最优订货周期和最优值的影响。

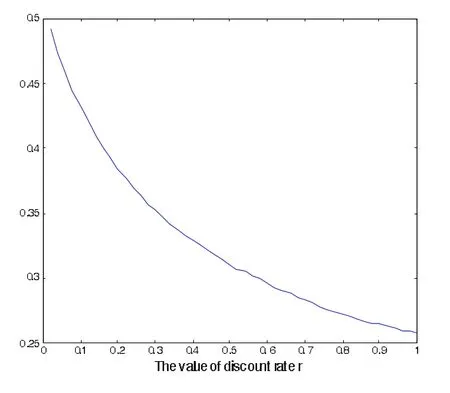
图1 折现率的变化最优解的影响

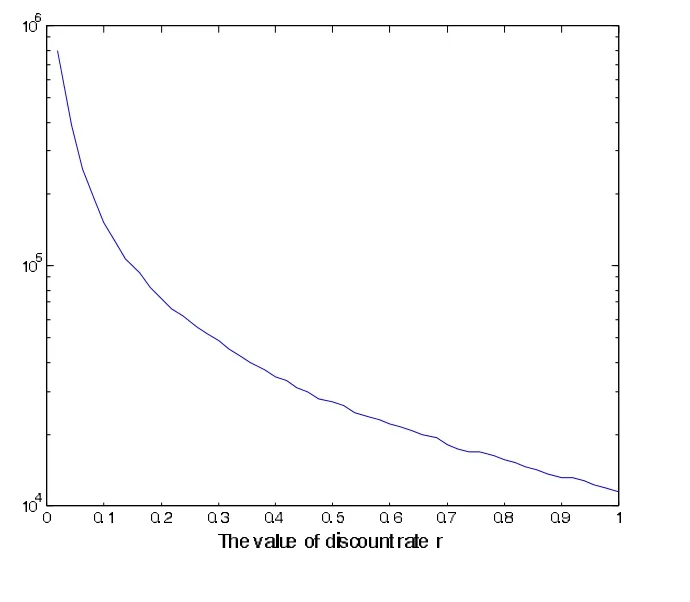
图2 折现率的变化对最优值的影响

由上图可以看出，最优解和最优值均随着折现率的增大而减小。

5 结束语

本文研究了非瞬间变质物品且考虑货币时间价值的二层信用支付的供应链库存问题，使得本模型更加贴近实际。通过理论分析得出的结果可以为供应链中零售商制定订货策略提供依据。本模型忽略了顾客需求的变化、缺货以及供应链企业竞争等因素，我们可在本模型的基础上对这些因素进行进一步的研究。

[1]Y.F.Huang.Optimal retailer’s ordering policies in the EOQ model under trade credit financing[J].Journal of the Operational Research Society,2003，54：1011-1015.

[2]J.J.Liao.An EOQ model with noninstantaneous receipt and exponentially deteriorating items under two-level trade credit[J].International Journal of Production Economics,2008，113：852-861.

[3]C.T.Chang,J.T.Teng,M.S.Chern.Optimal manufacturer’s replenishment policies for deteriorating items in a supply chain with up-stream and down-stream trade credits[J].International Journal of Production Economics,2010，127：197-202.

[4]G.C.Mahata.An EPQ-based inventory model for exponentially deteriorating items under retailer partial trade credit policy in supply chain[J].Expert Systems with Applications,2012，39：3537-3550.

[5]闵杰，周永务，刘耀玺，等.时间需求基于两层次信用支付策略的供应链库存模型[J].系统工程理论与实践，2011，31（2）：262-269.

[6]潘义前，劳毅慧.基于二层信用支付下的变质物品库存模型[J].数学的实践与认识，2011，41（10）：11-19.

[7]K.J.Chung,S.D.Lin.The inventory model for trade credit in economic ordering policies of deteriorating items in a supply chain system[J].Applied Mathematical Modelling,2011，35：3111-3115.

[8]K.J.Chung,J.J.Liao.The optimal ordering policy in a DCF analysis for deteriorating items when trade credit depends on the order quantity[J].International Journal of Production Economics,2006，100：116-130.

[9]K.J.Chung,J.J.Liao.The optimal ordering policy of the EOQ model under trade credit depending on the ordering quantity from the DCF approach[J].European Journal of Operational Research,2009，196：563-568.

[10]J.J.Liao,K.N.Huang.An Inventory Model for Deteriorating Items with Two Levels of Trade Credit Taking Account of Time Discounting[J].Acta Applicandae Mathematicae,2010，110：313-326.