第一性原理研究稀土掺杂ZnO结构的光电性质*

李泓霖 张仲† 吕英波 黄金昭 张英 刘如喜

1)(济南大学物理科学与技术学院,济南 250022)

2)(山东大学威海分校空间科学与物理学院,威海 264209)

(2012年5月9日收到;2012年9月26日收到修改稿)

1 引言

ZnO是II-VI族直接宽带隙氧化物半导体材料,室温下能隙宽度为3.37 eV,具有高达60 meV的激子束缚能、稳定的化学性质以及优良的光电特性等优点,在太阳能电池、平板显示器、半导体激光器以及透明导电薄膜等方面有着广阔的应用前景,已成为继GaN之后在短波长半导体材料研究领域的新热点[1−3].目前,人们主要以ZnO薄膜光电器件方面的研究为重点,主要采用的研究方法是通过掺杂不同类型的元素对其进行光电改性.例如,ZnO是本征n型半导体,掺入H或N等受主元素则可得到导电性能较好的p型ZnO材料[4−7];掺杂Fe,Co,Ni,Mn等过渡族金属元素的ZnO则转换为良好的稀磁半导体(diluted magnetic semiconductors,DMS)材料,可用于制作电子自旋或场发射方面的器件[8];而Cu掺杂ZnO后其电子结构和铁磁稳定性发生了显著的变化[9];进一步通过对ZnO单掺Ni,共掺(Ni,Al)或(Ni,Li)等杂质的计算结果表明,Ni掺杂的位置影响着ZnO铁磁性和反铁磁性的相对变化,在共掺的情况下,其铁磁性显著增强[10].因此,对ZnO掺杂各种类型元素的理论及实验研究已成为该领域的一个研究热点,并且通过掺杂这种方式能够使人们对ZnO掺杂结构的光电性质的变化机理有一个新的认识[11−15].

由于镧系稀土元素具有独特的最外层电子结构,现已被广泛运用于电磁器件和发光材料的生产中,是ZnO掺杂体系研究的新热点.Lang等[16]通过ZnO薄膜共掺稀土Eu,Er发现掺杂体系的光致发光谱出现了明显的变化,其蓝光发射峰的强度随着Er含量的增加而增加;Minami等[17]利用实验方法研究了稀土元素(Sc,Y)掺杂ZnO,发现其为n型掺杂,掺杂后电阻率减小,导电性增强;Kaur等[18]通过实验方法研究了Y掺杂ZnO的光电学特性.Gd具有独特的闪光特性,可用于荧光薄膜或者其他发光材料的制备中.在稀土共掺Gd的情况下,Gd可作为敏化剂,增大吸收截面而提高激活剂的发光强度[19−22].此外,在近红外光谱区,Er是常见的掺杂元素之一,这是因为其4I15/2→4I11/2和4 F7/2→4 I11/2的跃迁易被半导体激光二极管所激发.因此我们选择Er和Gd作为掺杂的两种元素具有实际的应用价值.

本文以ZnO作为基体,稀土元素Er和Gd作为掺杂原子,利用第一性原理超软赝势方法(USP),对稀土Er,Gd掺杂ZnO前后晶体的能带、电子态密度和光学性质进行了对比研究,初步揭示了通过ZnO掺杂稀土元素改变光电性质的内在原因,为实验工作提供了理论参考.

2 模型构建及计算方法

ZnO晶体结构在热力学稳定时是六方纤锌矿型,其空间群为C(P63mc),晶格常数a=b=0.3249 nm,c=0.5206 nm,c/a=1.602,比理想的六角柱密堆积结构的1.633稍小,α=β=90°,γ=120°.C轴方向的 Zn—O键长为 0.1992 nm,其余轴向为0.1973 nm,ZnO晶胞是由氧和锌的六角密堆积结构互相反向套构而成.本次计算是基于本征ZnO原胞沿a,b和c基矢扩展一个单位得到的2×2×2超晶胞,共含16个Zn和16个O原子[23].本文对稀土掺杂ZnO使用原子替代法.单掺杂时,在图1(a)ZnO超晶胞模型中的X处用Er原子或Gd原子替代一个Zn原子,形成浓度为6.25%的掺杂ZnO结构.对于双元素共掺的(Er,Gd)-ZnO,基于Er和Gd之间可能存在着相互作用,为降低两元素之间的互作用力,在图1(b)的X,Y处分别用两个稀土原子替代Zn原子,形成浓度为12.5%的共掺杂ZnO结构.

图1 (a)单掺Er或Gd时稀土元素所在的位置;(b)共掺(Er,Gd)时稀土元素所在的位置

文中所有的计算工作都是由Materials Studio软件中的Castep(cambridge serial total energy package)软件包完成[23].Castep是利用第一性原理,以密度泛函理论(DFT)和分子动力学理论为基础的软件包,适宜于计算具有周期性结构的材料.电子-电子相互作用的交换和相关势由局域密度近似(LDA)或广义梯度近似(GGA)进行校正[24,25].本文采用周期性边界条件,用GGA的Perdew-Burke-Ernzerhof(PBE)来处理电子间的交换关联能.先对所建立的模型进行几何优化,使其得到最优的几何结构后再进行相关结构和光学特性的计算.采用超软赝势来描述离子实与价电子之间的相互作用势.选取Zn,O,Er和Gd原子的价电子组态分别为:Zn 3d104s2,O 2s22p4,Er 4f125s25p66s2,Gd 4f75s25p65d16s2.截断能为340 eV,自洽收敛能的精度平均每个原子为1.0×10−5eV,K点取值为4×4×2,计算都在倒易空间中进行.

3 计算结果及分析

3.1 能带结构和态密度分析

图2是未掺ZnO和稀土元素掺杂后的能带结构.通常关注的是由掺杂所引起的费米能级附近发生的变化,因为结构的性质主要由这部分所决定.所以为了清楚起见,图2只给出了−8—8 eV部分的能带结构,并以费米能级作为能量零点.从图2(a)中未掺ZnO的能带图可以看出,价带顶和导带底都位于G点处,说明ZnO是直接带隙半导体,带隙为0.73 eV.这一计算结果与关丽等[26]得到的计算结果(0.72 eV)十分接近,但是与ZnO的实验禁带值3.37 eV差距明显,这是因为采用密度泛函理论计算晶体的结构时,禁带普遍偏低.对于本文的本征ZnO结构而言,由于Zn 3d态的能量被过高估计,使得其与O 2p态之间的互作用增强,价带带宽增大,因此带隙偏低.但理论计算与实验之间带隙的偏差并不影响对ZnO电子结构及相关性质的理论分析.由图2可以看出,掺杂稀土原子后导带部分的结构比较相似,与本征ZnO相比导带变化趋于平缓,掺杂ZnO的费米能级EF上移进入导带内,显然这是由于稀土元素的掺入使得导电载流子数目增多所引起,导带底附近的量子态基本已被电子所占据,发生载流子的简并化,形成简并半导体.这表明稀土Er,Gd掺杂ZnO是一种n型掺杂,掺杂后导带附近有额外的电子形成施主缺陷.另外从能带结构图中可以看出,稀土掺杂后ZnO结构的带隙变宽,图2(b),(c)和(d)的带隙分别达到1.16,1.18和1.21 eV.实验方面,Chen等[12]利用溶胶-凝胶法制备了稀土La掺杂的ZnO薄膜,证实了随着La掺入ZnO晶格含量的增加其带隙随之增大的趋势[27].

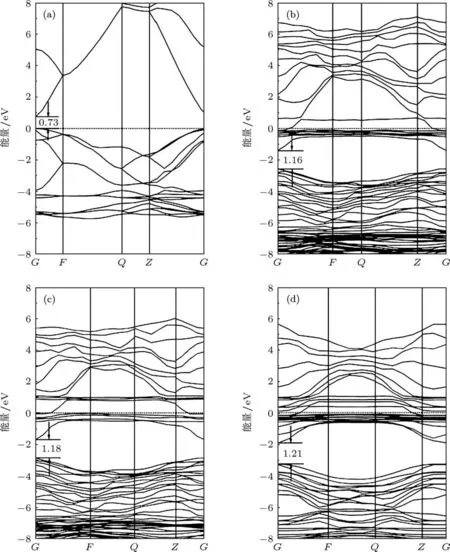
图2 稀土掺杂前后ZnO的能带结构 (a)ZnO;(b)Er-ZnO;(c)Gd-ZnO;(d)(Er,Gd)-ZnO

图3为掺杂前后ZnO的总态密度(TDOS)以及分态密度图(PDOS).从图3(a)可以看出,纯净ZnO的价带由三部分组成:−4.5—0 eV的上价带,这一部分主要由O 2p态和少量的Zn 3d态耦合而成;其次,在−6.0—−4.5 eV范围内的能带,这一部分主要由Zn 3d态和部分O 2p态形成;最后,在价带下方−18—−16 eV范围内还存在一部分孤立能带,这是由O 2s态形成的.对于导带部分,其主要由Zn 4s态和O 2p态形成,这和ZnO的总态密度相符合.图3(b)—(d)是稀土元素掺杂后ZnO的态密度图.总体而言,掺杂后费米能级上移并进入导带内,显示n型导电性,这是由于稀土元素的掺入使得导电载流子增多所引起的.从图3(b)可以看出,掺Er后在费米能级附近出现了杂质能级,这些杂质能级是由Er的4f态所形成.另外,在上导带部分(3—7 eV)和下价带部分(−17—−24 eV)的能带结构与纯净ZnO的相比出现展宽,局域性减弱,这是由于掺杂稀土后Er的5p态影响所致.这些由掺杂原子所引入的新能带与其他能带之间的相互作用很微弱,对掺杂材料的整体性能影响很小.图3(c)为掺Gd后的ZnO态密度图,可以看出这和Er掺杂结构有两点不同:首先,费米能级附近出现了两处杂质能带,分别位于−1.0—0.7 eV和0.7—2.2 eV,这是由Gd的4f态形成,其密度小于掺Er后ZnO在费米能级附近的杂质能带;另外,Gd的5d态还显示出了对ZnO上导带3.3—6.8 eV的部分贡献.图3(d)为Er和Gd共掺时的态密度图,可以看到费米能级附近依然存在杂质能带而强度有所不同.Er和Gd的s轨道电子态密度对ZnO晶体的价带与导带都只有很小的贡献,并且只在更深能级处(＜−40 eV)有作用,所以在此可忽略不计.通过以上分析,稀土原子Er,Gd替位Zn掺杂ZnO后能带数目增多,并且其4f电子态对ZnO掺杂结构的性质起着主要的影响.实验上Bai等[15]通过对ZnO掺Er纳米晶进行近红外(976 nm)激发,发现掺杂样品出现了上转换发光现象,其光致发光谱由绿光(520—570 nm)和红光(650—690 nm)组成,这正是由ZnO基体中Er3+的4f跃迁引起.未掺ZnO的费米能级位于价带顶;掺杂稀土后,电子态发生简并而费米能级上移进入到导带.掺Er后费米能级与导带底相差约1.41 eV;掺Gd后相差约1.69 eV;共掺时相差约1.96 eV.这表明稀土掺杂ZnO后体系呈现金属性,掺Gd比掺Er表现出更强的金属性,共掺时达到最大.

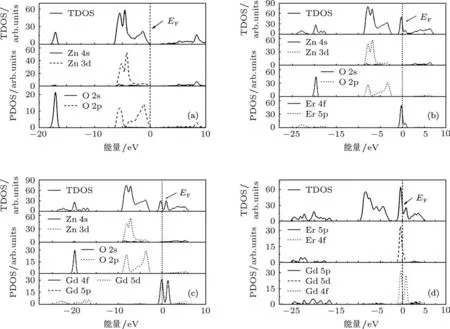
图3 稀土掺杂前后ZnO的态密度图 (a)ZnO;(b)Er-ZnO;(c)Gd-ZnO;(d)(Er,Gd)-ZnO

3.2 稀土掺杂前后ZnO光学性质的研究

固体的宏观光学响应函数在线性响应范围内一般可由光的复介电常数ε(ω)=ε1(ω)+iε2(ω)来描述.其中ε1=n2−k2,ε2=2nk分别为介电函数的实部和虚部.根据Kramers-Kronig色散关系和直接跃迁概率的定义可以推导出晶体介电函数的实部ε1,虚部 ε2,吸收系数 I(ε),反射系数 R(ε)和能量损失L(ε)等.在这里直接给出相关的结果[28]:

其中,C和V分别表示导带和价带,BZ是第一布里渊区,¯h为狄拉克常量,K为倒格矢,ω为角频率,|e·MCV(K)|2为动量矩阵元.以上各式是理论分析晶体能带结构和光学性质的依据,反映了因电子跃迁产生光谱的发光机理.这种分析方法不仅能够用以表征材料的物理结构特性,而且更易于与物理作用过程的微观电子结构和微观模型相联系.

图4(a)是纯净ZnO和稀土掺杂后的介电函数虚部ε2和实部ε1.纯净ZnO的虚部ε2有三个主要峰,分别出现在0.85,6.33和10.31 eV处.0.85 eV处的峰主要由价带顶的O 2p态和导带低处的Zn 4s态之间的光学跃迁引起.6.33 eV处的峰主要是由Zn 3d态和O 2p态之间的跃迁引起.10.31 eV处的峰则是由Zn 3d态和O 2s态之间的跃迁所致[29,30].稀土掺杂后,存在三个峰,分别位于0.5,2.5,8.0 eV附近,共掺杂情况下的介电函数虚部ε2相比单掺体系略微向低能方向移动,并且其值在低能部分整体上大于纯净和单掺Er或Gd的ZnO.在0—2 eV范围内掺杂晶体的ε2变化明显,并且在0.5 eV附近出现第一个峰.对于实部ε1,峰位变化与虚部相似,强度有所区别.共掺ZnO在2—12 eV区域之间取值最低,其余部分最高.总体而言,纯净和掺杂ZnO体系的介电函数在低能部分差别较大,当能量大于10 eV后变化趋于一致,这主要归因于Zn和O之间的光学跃迁,包括O 2p和Zn 3d态之间或者O的孤立态2s和Zn 3d态之间的跃迁,这可以从图3中的ZnO的分态密度图看出.

图4(b),(c)和(d)为掺杂前后ZnO的光学性质谱.其中图4(b)为光学吸收谱,纯ZnO的吸收谱有三个主要的峰,分别位于5.1,8.2和11.4 eV处.纯净ZnO的光吸收边约为0.7 eV,对应于图2中所计算的带隙,即价带顶电子跃迁到导带底所需的能量.稀土掺杂后光吸收边向高能方向移动,出现蓝移现象,这与实验结果相一致[31],主要是由于Burstein-Moss效应所引起[32].我们知道ZnO是一种天然n型半导体材料,当其掺入稀土元素后,导带附近将会形成额外的载流子—–电子而使ZnO的费米能级上移进入导带.由于导带底到费米能级处都会被电子填充,所以跃迁过程将会在价带和导带中的费米能级以上发生而不是导带底.这使得吸收边朝着高能方向移动,进而产生蓝移.掺杂ZnO的吸收跨度要比纯净ZnO大,但是吸收主峰明显小于纯净的ZnO.吸收峰主要来源于激发态的价带电子向导带跃迁的过程,而吸收峰的减弱则表明了由于稀土元素的掺入使得这种跃迁过程的减少.当能量高于18 eV后,纯净ZnO几乎不再吸收能量,而掺杂体系还存在着不同程度的吸收,这主要是由于稀土元素丰富的能级结构使得掺杂后ZnO的吸收得到显著的改善.未掺杂ZnO的吸收系数主峰在11.4 eV处,掺杂稀土元素Er,Gd后的吸收系数峰值有不同程度的减小.掺Er时,其21.3和28.8 eV处的两个峰值是由Er原子的5p态电子跃迁到导带底形成的;掺Gd时,其20.8和24.6和27.9 eV处的峰同样是由Gd原子的5p电子跃迁到导带底所形成.图4(c)为掺杂前后ZnO反射率的变化.在可见光区,共掺的吸收系数和反射系数都较高.纯净ZnO的反射率主峰在15 eV左右,掺杂后主峰的位置都有向低能方向移动的现象,共掺条件下幅度最大,高能区域的变化趋势相似.掺入稀土原子后高能区域的反射率和吸收率都不同程度地小于纯净的ZnO,这说明掺入稀土原子后紫外光区的透过率增加.能量损失谱是描述电子在通过均匀的电介质时能量的损失情况的物理量[29].从图4(d)可以看出,纯ZnO的能量损失峰在15.2 eV附近,接近于实验值18.8 eV[33].掺杂情况下,能量损失谱出现红移,共掺红移的程度最大,而且能量损失峰与反射谱的急剧下降相对应.

图4 掺杂前后ZnO的 (a)介电函数;(b)吸收谱;(c)反射率谱;(d)能量损失谱

4 结论

运用第一性原理研究了稀土元素Er,Gd掺杂ZnO的能带结构与光学性质,讨论了掺杂稀土元素Er和Gd对ZnO体系的能带结构和光学性质的影响.计算结果表明掺杂后费米能级附近出现了由掺杂原子贡献的自由载流子,费米能级进入导带,明显提高了掺杂体系的电导率.对光学性质的计算显示出ZnO与Er-ZnO,Gd-ZnO和(Er,Gd)-ZnO的介电函数虚部有明显的差异,共掺条件下的介电虚部在低能部分比纯净和单掺的大;由于Burstein-Moss效应,使得掺杂体系的吸收边出现蓝移现象,并且掺杂ZnO在可见光区的吸收系数和反射率都比纯净ZnO高,而能量损失谱则出现红移现象.

[1]Zhou Z,Komori T,Ayukawa T,Yukawa H,Morinaga M,Koizumi A,Takeda Y 2005 Appl.Phys.Lett.87 091109

[2]Lang J,Han Q,Yang J,Li C 2010 J.Appl.Phys.107 074302

[3]Tang Z K,Wong G K L,Yu P 1998 Appl.Phys.Lett.72 3270

[4]Zhang JK,Deng S H,Jin H,Liu Y L 2007 Acta Phys.Sin.56 5371(in Chinese)[张金奎,邓胜华,金慧,刘悦林2007物理学报56 5371]

[5]Mujdat C,Yasein C,Saliha I 2007 Phys.Stat.Sol.C 4 1337

[6]Deng B,Sun H Q,Guo Z Y,Gao X Q 2010 Acta Phys.Sin.59 1212(in Chinese)[邓贝,孙慧卿,郭志友,高小奇2010物理学报59 1212]

[7]Zhou C J,Kang J Y 2006 Chin.J.Lumin.27 917(in Chinese)[周昌杰,康俊勇2006发光学报27 917]

[8]Xia C H,Zhou M,Han X Y,Yin P F 2011 Mater.Rev.25 11

[9]Huang L M,Rosa A L,Ahuja R 2006 Phys.Rev.B 75 75206

[10]Pei G Q,Xia C T,Wu B,Wang T 2008 Comput.Mater.Sci.43 489

[11]Liu Y,Tian T,Wang B 2008 J.Appl.Phys.103 056104

[12]Chen J T,Wang J,Zhang F,Zhang G A,Wu Z G,Yan P X 2008 J.Cryst.Growth 310 2627

[13]Liu H,Yang J,Hua Z,Zhang,Yang L,Xiao L 2010 Appl.Surf.Sci.256 4162

[14]Jang Y R,Yoo K H,Ahn J S,Kim C,Park S M 2011 Appl.Surf.Sci.257 2822

[15]Bai Y F,Wang Y X,Yang K,Zhang X R,Song Y L,Wang C H 2008 Opt.Commun.218 5448

[16]Lang JH,Li X,Yang JH,Yang L L 2011 Appl.Surf.Sci.257 9574

[17]Minami T,Yamamoto T,Miyata T 2000 Thin Solid Films 366 63

[18]Kaur R,Singh A V,Mehra R M 2004 Mater.Sci.Poland 22 201

[19]Liu L,Yu P Y,Ma Z,Mao S S 2008 Phys.Rev.Lett.100 127203

[20]Seo S Y,Lee S,Park H D,Shin N,Sohn K S 2002 J.Appl.Phys.92 5248

[21]Bae J S,Jeong J H,Yi S S,Park J C 2003 Appl.Phys.Lett.82 3629

[22]Garcia-Murillo A,Luyer C L,Garapon C 2002 Opt.Mater.19 161

[23]Keiji W,Masatoshi S,Hideaki T 1999 J.Electroanal Chem.473 250

[24]Vanderbilt D 1990 Phys.Rev.B 41 7892

[25]Perdew J P,Burke K,Ernzerhof M 1996 Phys.Rev.Lett.77 3865

[26]Guan L,Li Q,Zhao Q X,Guo J X,Zhou Y 2009 Acta Phys.Sin.58 5634(in Chinese)[关丽,李强,赵庆勋,郭建新,周阳2009物理学报58 5634]

[27]Deng S H,Duan M Y,Xu M,He L 2011 Physica B 406 2314

[28]Shen X C 1992 The Optical Properties of Semiconductor(Beijing:Science Press)p24(in Chinese)[沈学础1992半导体光学性质(北京:科学出版社)第24页]

[29]Duan M Y,Xu M,Zhou H P,Shen Y B,Chen Q Y,Ding Y C,Zhu W J 2007 Acta Phys.Sin.56 5359(in Chinese)[段满益,徐明,周海平,沈益斌,陈青云,丁迎春,祝文军2007物理学报56 5359]

[30]Zhang X D,Guo M L,Li W X,Liu C L 2008 J.Appl.Phys.103 063721

[31]Lan W,Liu Y P,Zhang M,Wang B,Yan H,Wang Y Y 2007 Mater.Lett.61 2262

[32]Anomalous E B 1954 Phys.Rev.93 632

[33]Lu J G,Fujita S,Kawaharamura T,Nishinaka H,Kamada Y,Ohshima T,Ye Z Z,Zeng Y J,Zhang Y Z,Zhu L P,He H P,Zhao B H 2007 J.Appl.Phys.101 083705