压印接头拉剪强度的有限元模拟
2013-12-11杨慧艳何晓聪丁燕芳
杨慧艳,何晓聪,周 森,丁燕芳
(昆明理工大学机电工程学院,昆明650500)
0 引 言
近年来,由于汽车工业技术的迅速发展和日趋激烈的竞争,铝、镁合金等轻量化材料在汽车车身上的应用越来越多,这就给轻型材料之间的连接带来了新的问题。传统的连接技术(如点焊)很难或不能实现这些材料的连接。压印连接是通过专用的压印连接模具在外力作用下,迫使被连接材料在连接点处产生材料流动,形成一个相互镶嵌的塑性变形的连接接头。该技术可以很好地实现铝、镁等材料的连接,并能解决异种板料、镀层板及多层材料等的连接问题,而且该技术简单、高效、环保、易于实现自动化,将成为下一代先进汽车制造中的一种重要连接方法。
国内外许多学者已对压印连接技术进行了多方面的研究,并取得了一系列研究成果。何晓聪[1-2]从工艺参数、动态工艺模拟、接头强度和振动特性等方面综述了压印连接技术的发展状况,并研究了变差系数法在预测压印接头强度方面的应用,指出变差系数法在产品质量评估等方面具有重要意义;De[3]等通过有限元模拟研究了模具几何尺寸对颈部厚度和互锁嵌入量的影响;Jacek[4]研究了模具几何尺寸以及压印连接过程中诸如冲压力等对连接接头强度的影响,同时从微观角度确定了接头塑性应变区域的应力分布;Varis[5-6]等根据板料尺寸选择不同的模具类型,并利用有限元模拟分析方法得到了一种模具选择程序;Lee[7-8]等建立了模具尺寸参数和强度的数学模型,使得根据所需强度来得到模具尺寸成为可能,这对指导设计和生产具有重大意义;周云郊等[9]采用试验和有限元模拟相结合的方法对钢铝组合板材的压印连接件进行了几何工艺参数的多目标优化;龙江启等[10]基于神经网络提出了压印接头力学性能预测的方法。但目前针对压印连接技术的研究大多停留在连接工艺上,关于压印接头拉剪强度及其破坏形式的预测研究较少。为此,作者采用有限元方法对钢-钢和铝-铝压印接头的拉剪过程进行有限元模拟,预测了接头的强度和失效模式,提出了压印接头拉剪强度的一种有限元预测方法,并推导出强度理论公式,最后进行了试验验证,可以为实现结构轻量化的压印接头设计提供依据。
1 试样制备与试验方法
1.1 试样制备
两种不同的压印接头材料分别为5052铝合金和SPCC钢,相关参数如表1所示。
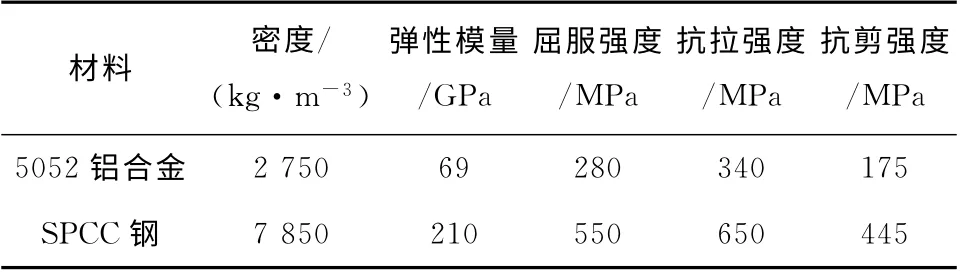
表1 压印接头材料的参数Tab.1 Parameters of clinched joint materials
在RIVCLINCH 1106P50型压印连接设备上制备压印接头试样,如图1所示。制备铝-铝压印接头时选用的上模型号为SR5010,下模型号为SR60314,上、下板料尺寸均为110mm×20mm×2mm;制备钢-钢压印接头的上模型号为SR5210,下模型号为SR60310,上、下板料尺寸均为110 mm×20 mm×1mm,试样搭接部分长度为20mm,在搭接部中央进行单点压印连接,压印力为0.65MPa。
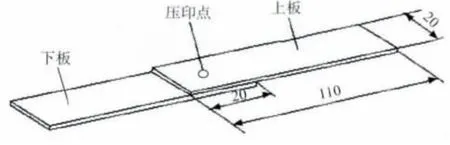
图1 压印接头试样示意Fig.1 Schematic diagram of clinched joint
1.2 试验方法
在MTS landmark型疲劳试验机上对压印接头进行拉伸-剪切试验,拉伸速率为5mm·min-1。考虑到单搭试样夹持后会产生作用力不同轴的情况,在试样两端安装相应厚度的垫片以避免产生弯矩,试样装夹如图2所示,图3为压印接头的破坏过程。

图2 试样装夹Fig.2 Sample set up

图3 压印接头破坏过程Fig.3 Neck fracture process of clinched joint
试样的载荷-位移曲线如图4 所示。其中,铝-铝试样组中6个最大载荷的平均值为1 446.6N,标准差为29.2N,钢-钢试样组中6个最大载荷的平均值为2 447.6N,标准差为49.3N。两组试样的失效形式均为上板颈部最薄处断裂。

图4 两种压印接头的载荷-位移曲线Fig.4 Load-displacement curves of two clinched joints
2 有限元模型的建立
采用有限元软件ANSYS对压印接头的拉伸-剪切过程建立模型并进行有限元模拟。为了得到更精确的有限元分析结果,将铝合金和钢作为非线性材料考虑。在接头的剪切拉伸过程中,能量和载荷依靠接触和摩擦在不同材料间传递,因此有限元模型中充分考虑材料间的接触和摩擦。
2.1 模型的建立及边界条件
根据图5铝-铝压印接头的截面形貌,按截面形状和尺寸建立接头的有限元模型,如图6所示。由于接头沿中心面对称,故取1/2模型进行计算。网格划分采用智能尺寸的自由网格划分,智能等级为6。采用同样的方法根据实际接头的截面建立钢-钢压印接头的有限元模型。

图5 铝-铝压印接头的截面形貌Fig.5 Cross section of Al-Al clinched joint
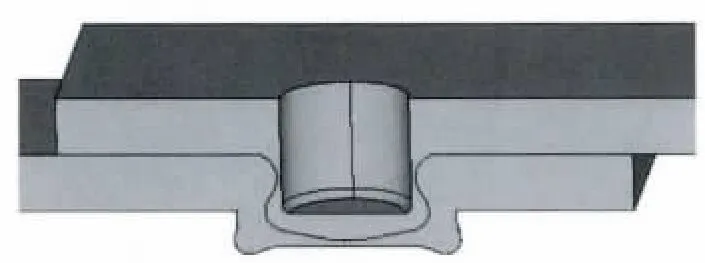
图6 铝-铝压印接头的有限元模型Fig.6 Finite element model of Al-Al clinched joint
材料模型选用双线性(Bilinear)材料模型。有限元模型中包含两部分:上板和上板,两者之间的接触类型选用ANSYS中面-面间的柔体-柔体接触类型,接触算法采用罚函数法。设定钢-钢之间的摩擦因数为0.2,铝-铝之间的摩擦因数为0.35。接触中选择库伦摩擦模型,库伦摩擦模型定义了一个等效剪应力τ:

式中:μ 为摩擦因数;p 为法向力;c为材料间的粘聚力。
在法向力p 作用下,剪应力达到临界值,相互接触的材料间开始发生滑动。这里采用程序默认的最大容许剪应力(1.0×1020MPa)。边界条件的设置与拉伸试验情况一致,通过模拟可以得到压印接头的失效模式和载荷-位移曲线。
2.2 有限元模拟结果
有限元模拟中的载荷以施加在接头一端面的位移(d)表示,铝-铝接头在整个拉伸过程中的有效位移为0.98mm。

图7 铝-铝压印接头在不同位移处的模拟结果Fig.7 Simulation results of AI-AI clinched joint at different displacements
由图7可见,在拉伸-剪切过程的初期,即位移d=0.125mm 时(相当于在接头上施加一个500N的静拉力),在接头颈部最薄的位置出现了环向的最大应力分布,且应力集中现象在最右端最严重;d=0.4mm时,接头出现变形,上下板之间沿竖直方向产生了缝隙,接头颈部发生少许倾斜;d=0.7 mm时,上下板缝隙明显增大,接头倾斜严重,上板在颈部被拉长并变薄,同时上板颈部开始屈服;d=0.98mm时,上下板缝隙进一步增大,颈部倾斜现象更严重,上板在颈部被进一步拉长,颈部径向尺寸明显减小,出现了明显的屈服现象并发生了严重的塑性变形。在整个拉伸-剪切过程中,上板由于尺寸和形状特点而出现了较大面积的高应力分布和应力集中。基于整个拉伸-剪切过程中接头变形和应力分布的分析,压印接头在颈部最薄处发生断裂,与拉伸-剪切试验结果一致。钢-钢压印接头与铝-铝压印接头具有相同的破坏过程。
由图8可以看出,铝-铝压印接头有限元模拟得到的载荷-位移曲线和试验所得载荷-位移曲线的变化趋势和大小基本一致。在拉伸-剪切过程的初期,载荷和位移均呈线性,进入屈服阶段时的载荷相当,但与试验值相比,模拟值的屈服阶段持续时间较长。这可能跟摩擦因数的设定有关,摩擦模型不能完全一致地模拟压印接头实际受力时的情况。
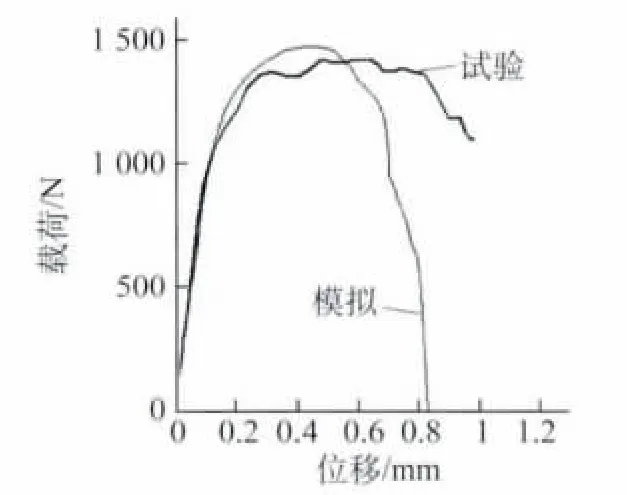
图8 试验和模拟得到的铝-铝压印接头的载荷-位移曲线Fig.8 Load-displacement curves of Al-Al clinched joint obtained from experiment and simulation
从图9可以看出,钢-钢压印接头的失效模式与铝-铝压印接头的失效模式相同,均为颈部发生严重的塑性变形,最终导致上板在颈部最薄处断裂失效,与试验结果吻合。
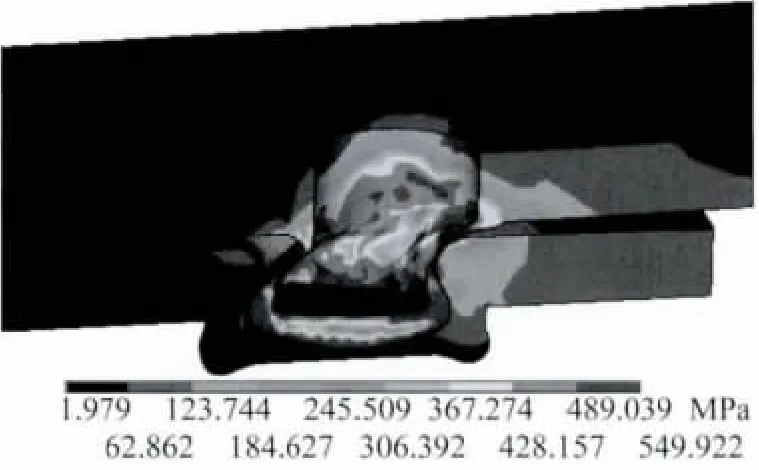
图9 钢-钢压印接头失效模式的模拟结果Fig.9 Simulated result of steel-steel clinched joint failure mode
由图10可以看出,钢-钢压印接头载荷-位移曲线的试验结果和模拟结果的变化趋势基本一致。
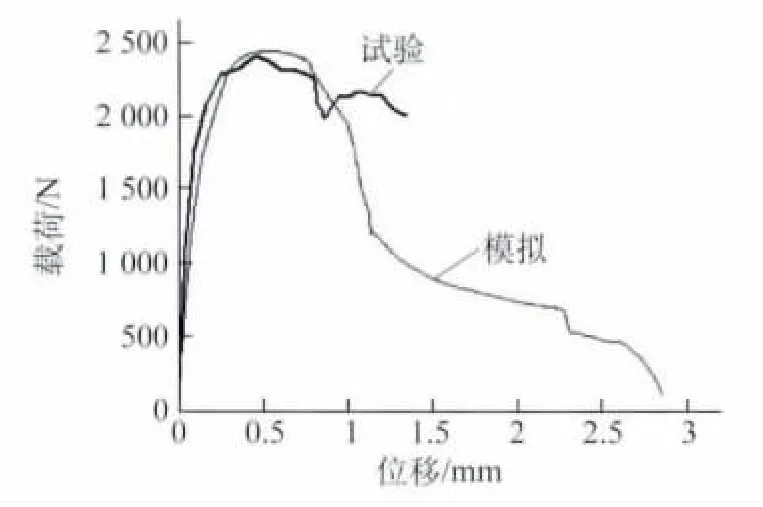
图10 试验和模拟得到的钢-钢压印接头的载荷-位移曲线Fig.10 Load-displacement curves of steel-steel clinched joint obtained from experiment and simulation
可见,模拟得到的两种压印接头的失效模式和接头强度与试验结果基本一致。
3 拉剪强度的预测
3.1 拉剪强度预测公式的推导
由压印接头的有限元模拟和试验结果可知,压印接头在拉伸-剪切载荷下的失效模式为上板在颈部最薄处被剪断。接头的拉剪强度从材料力学角度即为剪切强度,剪切力的大小取决于剪切面的面积和材料的剪切极限。压印接头的拉剪强度F 取决于上板颈部的截面积,可以由式(2)计算获得。
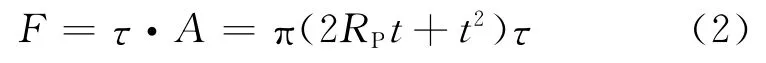
式中:τ为上板材料的剪切强度;A 为颈部截面积(图11);RP为模半径;t为颈部厚度。
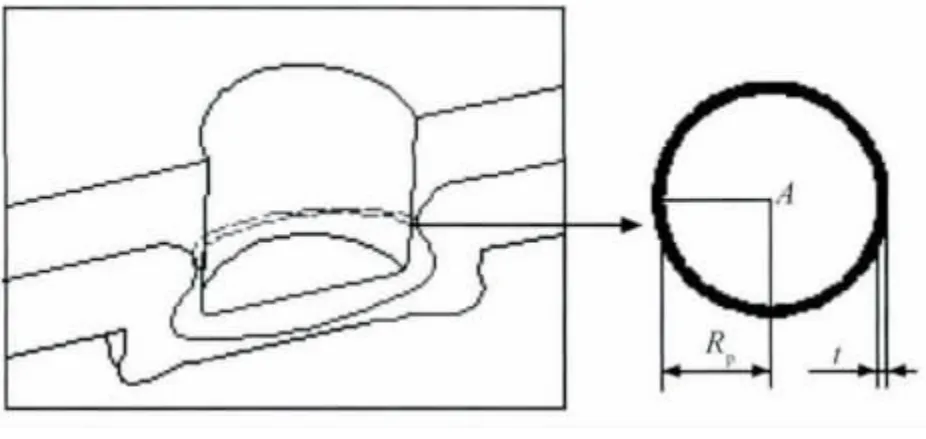
图11 拉伸-剪切试样的剪切面Fig.11 Shear section of clinched joint after tension-shear test
根据式(2)可以由测量的颈部厚度来预测压印接头的拉剪强度。
3.2 拉剪强度预测公式的验证
对于铝-铝压印接头,上模RP=2.5 mm,接头颈部厚度t=0.48mm,剪切强度τ=175 MPa,由式(2)计算出接头可以承受的剪切力为1 380.1N,与试验值(1 446.3N)相比,误差为4.6%;对于钢-钢接头,上模RP=2.6 mm,接头颈部厚度t=0.30mm,剪切强度τ=445 MPa,由式(2)计算出接头可以承受的剪切力为2 305.5 N,与试验值(2 447.6N)相比,误差为5.8%。可见,采用强度预测公式(2)能够很好地预测压印接头的拉剪强度。
由推导公式可知,压印接头拉剪强度主要取决于连接模具半径、上板材料强度和颈部厚度。
4 结 论
(1)根据压印接头的截面形状和尺寸,充分考虑材料之间的接触形式和摩擦而建立的有限元模型,能够较好地预测压印接头的拉剪强度和失效模式;铝-铝和钢-钢同种材料的压印接头在拉伸-剪切载荷下的失效形式为上板在颈部最薄处断裂。
(2)提出了压印接头强度的预测公式,两种接头预测值与试验值的误差分别为4.6%和5.8%。
(3)拉剪强度主要取决于连接模具半径、上板材料强度和颈部厚度。
[1]HE X.Recent development in finite element analysis of clinched joints[J].International Journal of Advanced Manufacturing Technology,2010,48(5/8):607-612.
[2]HE X.Coefficient of variation and its application to strength prediction of clinched joints[J].Advanced Science Letters,2011,4(4/5):1757-1760.
[3]DE PAULA A A,AGUILAR M T P,PERTENCE A E M,et al.Finite element simulations of the clinch joining of metallic sheets[J].Journal of Materials Processing Technology,2007,182(1/3):352-357.
[4]JACEK M.The analysis of lock forming mechanism in the clinching joint[J].Materials and Design,2011,32(10):4943-4954.
[5]VARIS J P.The suitability for round clinching tools for highstrength structural steel[J].Thin-Walled Structures,2002,40(3):225-238.
[6]VARIS J P.The suitability of clinching as a joining method for high-strength structural steel[J].Journal of Materials Processing Technology,2003,132(1/3):242-249.
[7]LEE C J,KIM J Y,LEE S K,et al.Design of mechanical clinching tools for joining of aluminium alloy sheets[J].Materials and Design,2010,31(4):1854-1861.
[8]LEE C J,KIM J Y,LEE S K,et al.Parametric study on mechanical clinching process for joining aluminum alloy and highstrength steel sheets[J].Journal of Materials Processing Technology,2010,24(1):123-126.
[9]周云郊,兰凤崇,黄信宏,等.钢铝板材压力连接模具集合参数多目标优化[J].材料科学与工艺,2011,19(6):86-99.
[10]龙江启,兰凤崇,陈吉清.基于神经网络无铆钉自冲铆接接头力学性能预测[J].计算机集成制造系统,2009,15(8):1614-1630 .
