基于聚类分析的多面函数拟合高程异常方法

2013-12-11孙佳龙焦明连梁青科

测绘通报 2013年2期

孙佳龙，焦明连，梁青科

(1.淮海工学院测绘工程学院，江苏连云港222001;2.山东里能鲁西矿业有限公司，山东济宁272053)

一、引言

随着GPS测量技术的不断发展和完善，求取高精度的高程异常在实际工程应用中越来越重要［1］。目前常用的高程异常拟合方法主要有多项式拟合法、移动二次曲面拟合法和多面函数拟合法等［2-3］。在拟合区域较小的情况下，一般拟合方法可以达到较高的精度，但由于这些方法未顾及似大地水准面的物理性质，拟合出的曲面只是高程异常的趋势面，与高程异常的实际数值存在一定差异［4］。多面函数在理论上可以以任意精度逼近任意复杂曲面，因此可以更加逼近实际的高程异常曲面［5］。但由于多面函数中心点的个数及中心点的选择对拟合精度影响较大，而其选择目前又尚无可靠的理论依据，为此本文提出了基于聚类分析的多面函数拟合法，对中心点的个数和中心点进行有效选取，使不同的中心点建立不同的多面函数模型，并从中选取最优模型作为最后的拟合模型。

二、多面函数

多面函数的理论依据是：任意数学表面与任意不规则的圆滑表面，总可以利用一系列的有规则的数学表面总和，以任意精度逼近。因此，由多面函数表示的残差高程异常为［4-5］

式中，aj是待定系数;q(x，y，xj，yj)是x和y的二次函数，其中心点在(xj，yj)处;n是中心点的个数;ζ可由二次式的和确定，故称多面函数。

用一组简单的解析函数的线性组合对这个曲面进行逼近，通常选择多元二次函数作为解析函数，其形式为［6］

式中，δ为圆滑因子，也称光滑系数，通常可取一小正数或零;b可选取某个非零实数，通常为或。

将式(2)写成误差方程，并用矩阵表示为

待定系数A可根据已知GPS/水准数据和地球重力场模型得到的残差高程异常，按最小二乘法计算，即

由此可根据系数A和式(1)求解其他点的残差高程异常。

三、基于聚类分析的多面函数

在式(1)中，由于选择的中心点个数n小于或等于已知的高程异常值的个数，因此需要对所有的高程异常值进行选取。人为选取高程异常值既耗时又费力，且容易出错。因此，合理有效地选取高程异常值，使这些高程异常能很好地表示该区域的高程异常变化就显得尤为必要。聚类分析是对样本进行分类的一种多元统计方法，是从样本中发现有用信息的一种有效手段［7-8］。由于聚类分析能够发现全局的分布模式及数据属性之间相互关系，因此，本文利用聚类分析方法，以欧氏距离作为相似性统计量。考虑到高程异常曲面不仅与样本点的地理位置有关，还与该点的高程异常值的大小有关，因此，本文以三维欧氏距离作为相似性统计量［7］，即

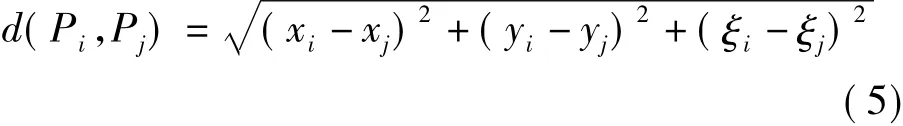
式中，xi、yi、ξi为Pi点的坐标和高程异常;d 为距离。由于高程异常的单位与坐标单位不同，在进行聚类分析之前需将高程异常数据进行规格化处理［9-10］

式中，i=1、2、3;P为规格化处理后的高程异常所对应的坐标和高程异常值。以某地区12个高程异常数据点为例，规格化处理后的各点的坐标和高程异常值如图1所示。

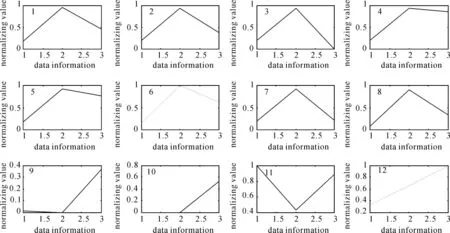
图1 规格化后的高程异常

从图1中可以看出，1、2和8号点的高程异常图形基本一致，4、5和6号点的残差高程异常图形也基本一致，而9和10号点的残差高程异常值的变化趋势也基本相同。因此，将以上几类数据分别聚类是合适的。11、12号点的残差高程异常与其他各点差异较大，当分类数较多时不宜归入其他类中。利用聚类分析，得到的聚类结果如图2所示。

图2 高程异常聚类树

从高程异常聚类树图中可以看出，1、2，4、5和9、10被首先归入一类，说明这几组数据相似性较大;8号点与1和2号点相似性也较大，因此8号点也被归入1和2号点这一类中;6号点与4和5号点也较为相似，因此6号点也被归入到4和5号点这一类;11和12号点相似性较小，直到最后所有数据被分为两类时，这两点才被归入一类。由此可以看出，聚类分析的结果与实际各点的相似情况基本吻合，因此利用聚类分析可以有效地对高程异常数据进行分类。

四、算例分析

某地区D级GPS控制网布设了17个观测点，对其进行了GPS观测和三等水准测量，利用GPS获得的大地高和水准测量得到正常高，以及17个GPS/水准点的高程异常。利用其中12个数据进行聚类分析，得到的分类数作为多面函数中心点的个数;从每个聚类中选取欧氏距离最长的高程异常作为多面函数中心点，构建多面函数。以另外5个点的数据作为外部检核。外符合精度为

式中，νi为检核点实测高程异常与拟合高程异常的差值;m为检核点个数。检核结果见表1。

表1 基于聚类分析的多面函数外部检核结果 mm

从表1中可以看出，分类数从2开始增大时，多面函数拟合的精度有所提高;当分类数为5时，精度最高，达到3.5 mm;随着分类数继续增加，精度又开始下降;当分类数为11时，精度最低，为152.8 mm。由此说明，通过对样本数据进行有效分类，并依此选取多面函数的中心点，可以有效地提高多面函数的拟合精度。为了综合评价基于聚类分析的多面函数的拟合精度，本文还利用同样的数据，以多项式曲面拟合、移动曲面拟合和多面函数拟合这3种常用的曲面拟合模型作为参考模型，比较各种模型之间的拟合精度(见表2)。

表2 拟合结果残差比较m

从表2中可以看出，移动二次曲面拟合的结果中，残差最大值为0.15 m，为各种拟合函数中的最大值，其标准差和外符合精度也都最大，说明移动二次曲面拟合的精度在4种方法中最差。5种评价指标都显示，聚类分析多面函数拟合的精度是最高的，其外符合精度最高，达到0.003 5 m。各个检核点的高程异常残差值如图3所示。