地面三维激光扫描仪的自检校模型研究

陈玮娴，袁 庆

(1.武汉市城乡建设委员会，湖北武汉430023;2.中铁第四勘察设计院，湖北武汉430063)

一、引 言

在地面三维激光的应用中，扫描仪的测量精度起着重要的角色，尤其在一些工程建设和变形监测中，为了使点云数据达到最大精度，必须进行扫描仪的检校。若因使用时的外力碰撞和其他未知因素造成仪器内部构造发生变化，则扫描结果可能含有系统性误差。然而，顾及时效和经济的因素，难以时常将仪器送回原厂商进行校正，因此需要发展一套地面三维激光扫描仪的自检校方法［1］，以使仪器的使用者可以在后续内业处理点云资料前先消除系统性误差从而提高测量的精度。本文以Y Reshetyuk［2］提出的球面-直角坐标系检校模型为基础(检校的6个系统误差分别为2个测距误差、3个轴系误差和1个竖直角尺度差)，对系统误差参数进行假设检验，并评定精度。通过模拟数值试验，验证该模型的可行性，并经实例计算得到较好的检校结果。

二、地面三维激光扫描仪自检校方法

1.自检校数学模型

自检校数学模型为

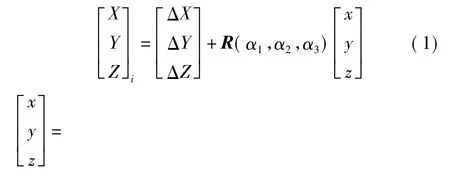
式中，(X，Y，Z)和(x，y，z)分别为外部坐标系下全站仪测量的平面靶标中心和扫描仪测得的扫描仪坐标系平面靶标中心;(ΔX，ΔY，ΔZ)为平移参数;R(α1，α2，α3)为两个坐标系之间的旋转矩阵，是3 个旋转角(α1，α2，α3)的函数;rs、φs、θs分别是扫描仪实际测量的径向距离、水平角和竖直角;K为测距加常数;R为测距乘常数;c为激光光束不垂直于扫描棱镜旋转轴误差，它对水平角的影响为c/cosθs;i为棱镜旋转轴倾斜误差，它对水平角的影响为itanθs;ξ为竖直角偏差;q为竖直角尺度误差［3］。由于从扫描仪中导出的是三维直角坐标(x，y，z)，因此可采用公式计算得到相应的极坐标系下坐标(rs，φs，θs)，并将式(1)线性化得

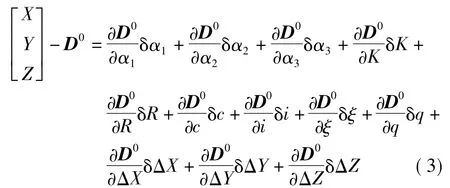
写成误差方程的形式为

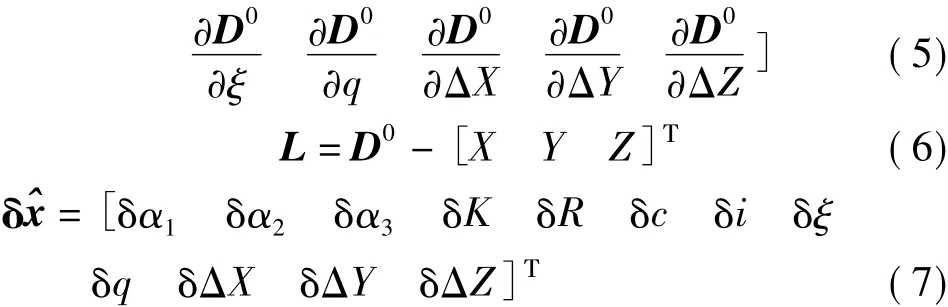
采用最小二乘平差，求得参数及其精度为

式中，x0为参数初值。

2.系统误差参数显著性检验

在确定检校模型的系统误差参数后，必须对参数进行显著性检测，以确定所选参数是否必需，这里采用t检验法［4-5］，构造统计量为

构造的原假设与备选假设分别为原假设

备选假设

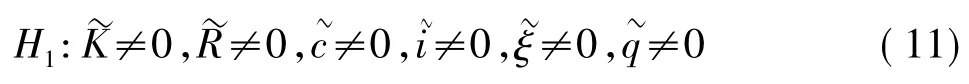
3.精度评定

通常需设置检查点，根据检查点坐标转换点位中误差评定精度，点位中误差计算如下

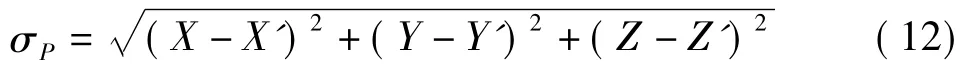
式中，(X'，Y'，Z')为扫描仪坐标转换至全站仪坐标系下的检查点坐标。

三、模拟数值验证及试验

1.模拟数值验证

首先，通过理论模拟测试，分析所使用的6个误差因子分别对扫描点云的坐标影响，图1分别为加入不同误差后对各扫描点坐标影响的向量图。扫描点间距：垂直视角40°，扫描角增量5°;水平视角40°，扫描角增量5°;距离2～3 m，距离增量0.1 m。

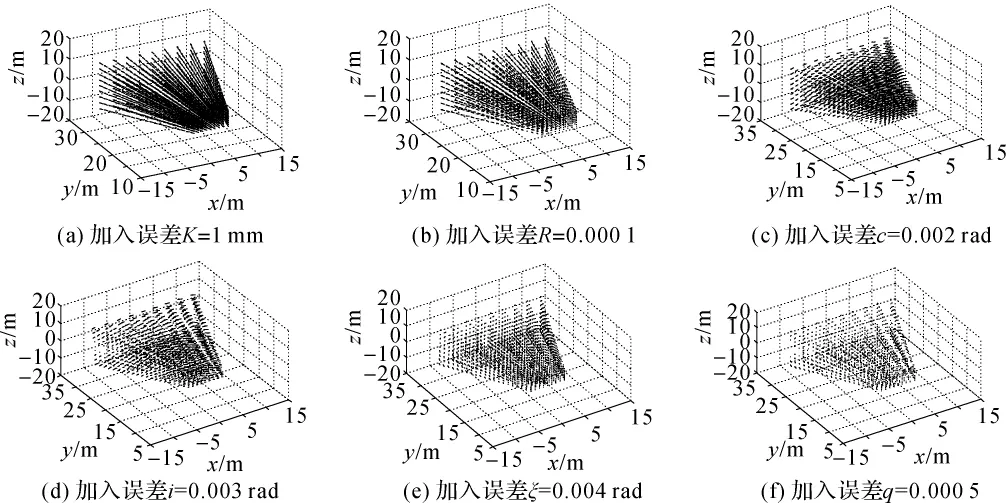
图1 加入系统误差后对扫描点坐标的影响

2.试 验

本试验采用Faro LS880地面三维激光扫描仪，该仪器标称点位精度为±3mm@25m，视场角为水平360°，竖直角为270°，采样率为120 000 点/s，扫描距离1～80 m。检校场布设在同济大学测量馆外墙面和台阶上，扫描场范围为15m×12m，经扫描拟合靶标后最终选择质量较好的26个点为检校点(18个墙面点，8个台阶点)，如图2所示。由于实际扫描距离小于10m，因此不考虑模型中的测距乘常数［6］。试验步骤如下：

1)布设平面靶标，靶标为10cm×10 cm的正方形白底反射标，中间是直径为7 cm的黑色圆，圆心贴有5 mm×5 mm的反射标，布设时贴于墙壁和台阶上呈前高后低的空间随机分布。

2)由全站仪测靶标中心反射标，并计算得到坐标值。

3)扫描仪全景扫描，确定扫描仪初始方向。

4)精扫每个靶标，选择拟合结果较好的靶标点，进行计算，解算结果见表1、表2。

图2 实地检校场

表1 第1次参数解算

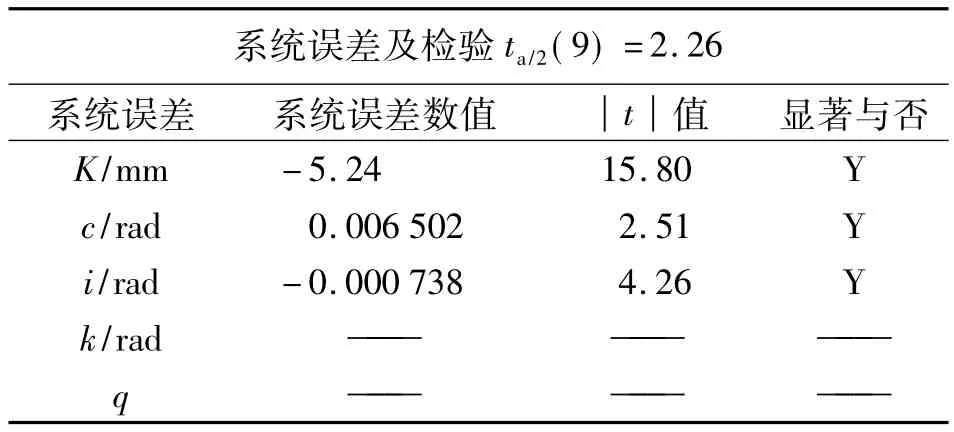
表2 第2次参数解算

由图3可以看出，检校后各方向坐标误差均小于3 mm。由式(9)计算得到经检校改正之后的平均点位误差为σp=1.617 mm，小于标称点位精度3 mm。所以依本文方案布设检校场切实可行。

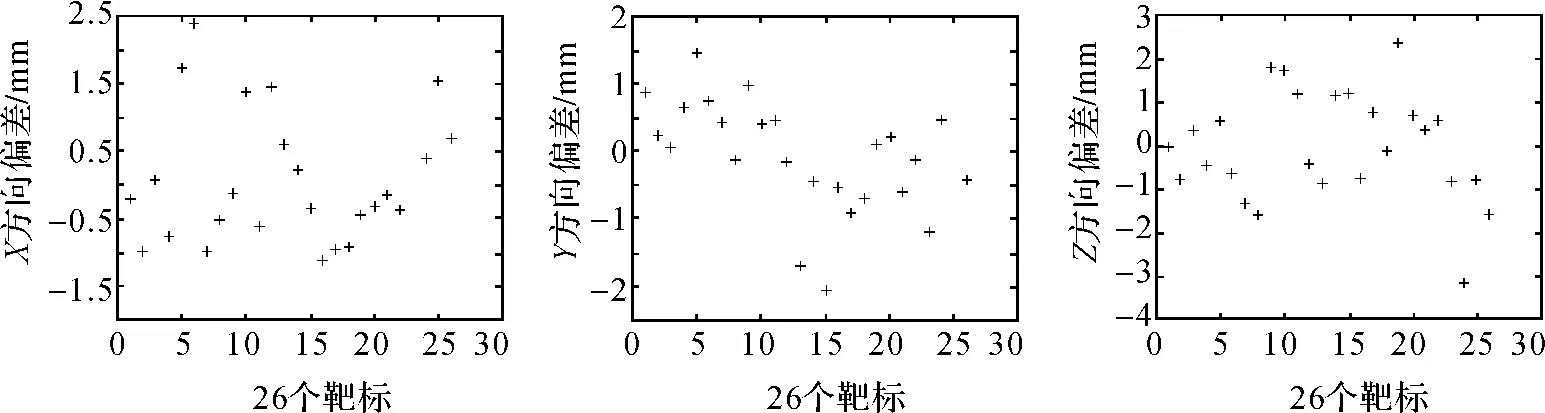
图3 各方向坐标差

四、结束语

本文首先通过理论模拟测试，对6个误差因子对扫描点的坐标影响进行分析;然后采用模拟数值对检校模型进行验证，证实该算法可靠性较高;最后通过实例计算，得到考虑系统误差因子的检校点点位误差为1.617 mm，小于标称点位精度3 mm，即检校后检查点点位精度提高，证明该方法切实可行。

［1］蔡汉龙.地面光达几何校正系统设计与实施［D］.台南：国立成功大学，2007：1-3.

［2］RESHETYUK Y.Investigation and Calibration of Pulsed Time-of-Flight Terrestrial Laser Scanners［D］.Stockoldm：Royal Institute of Technology，2006：87-90.

［3］LICHTI D D，FRANKE J.Self-calibration of the IQsun 880 Laser Scanner［J］.Optical 3-D Measurement Techniques，2005(1)：112-122.

［4］陶本藻，丘卫宁，黄加纳，等.误差理论与测量平差基础［M］.武汉：武汉大学出版社，2002.

［5］盛骤.概率论与数理统计［M］.北京：高等教育出版社，2001.

［6］张毅.地面三维激光扫描点云数据处理方法研究［D］.武汉：武汉大学，2008：50-51.