基于加速遗传算法的GPS变形监测单历元求解算法
2013-12-11张献州
王 建,张献州
(西南交通大学地球科学与环境工程学院,四川成都610031)
一、引 言
整周模糊度的精确求解是GPS变形监测[1-2]单历元解算中的关键问题,对获取高精度的变形量有着重要意义。国内外许多学者对遗传算法(genetic algorithm,GA)搜索整周模糊度进行了研究,如刘智敏详细阐述了遗传算法的编码方法和模糊度搜索过程[3];阳仁贵运用遗传算法搜索了单频单历元模糊度[4];吴万清对遗传算法联合模糊函数法进行了详细的研究[5]等。以上研究都是针对模糊度域进行操作,而模糊度具有整数特性,利用遗传算法搜索模糊度,取整时难免会存在精度损失。本文采用改进的二进制编码加速遗传算法(AGA),对监测点坐标进行全局最优搜索,当监测点坐标满足一定精度时,可利用直接计算法[6]快速准确地固定单历元双差模糊度。
二、加速遗传算法
GA是模拟生物进化过程中优胜劣汰规则与群体内部染色体信息交换机制的一类全局优化搜索算法[7]。传统遗传算法常出现早熟现象,且计算量较大,全局优化速度较慢,针对这些问题,文献[8]利用标准遗传算法搜索到的优秀个体来缩小变量的初始区间,构成一种变区间的AGA。此方法采用二进制编码形式,而该编码具有很强的杂交搜索能力,适用于较少变量和坐标域的优化搜索问题。
1.算法具体步骤
1)编码长度e的确定。编码长度决定了坐标的解算精度,加速遗传算法的变量区间不断缩小,可由区间大小[ai,bi]计算 e
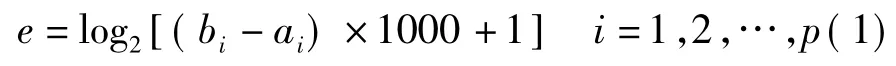
式中,p为未知变量的个数,取p=3;坐标搜索的精度精确到毫米。
2)初始种群的随机生成。种群规模n取200~400,生成 n组[0,1]区间上的均匀随机数,每组 p个,这些随机数将对应[ai,bi]的实数即为坐标候选值,相应的二进制编码则构成初始种群的染色体。
3)个体的适应度评价。由染色体对应的坐标候选值计算每个个体的适应度,并以此评价个体的优劣,调整进化的方向。此处适应度可依据模糊函数值计算

式中,ne为观测历元数;nf为观测频率数;ns为每历元双差观测值数;φmnobs为双差相位观测值;φmncal(xj,yj,zj)为坐标候选值计算的双差相位值。由式(2)知,模糊函数值越大,f(j)越大,个体适应度值越高。选择适应度最高的s个个体构成优秀个体,以自适应调整变量初始区间。
4)个体的选择操作。采用比例选择的方式,个体被选择的概率与其适应度值和群体适应度总和有关,适应度值越高的个体被选择的概率应越大。
5)个体的交叉和变异。交叉算子是体现遗传算法的全局搜索能力,而变异算子则反映遗传算法的局部寻优能力,两种算子是遗传算法的核心。此处采用两点变异的方式,以增强群体的多样性,避免陷入局部最优;概率通过动态自适应方式确定,对于适应度值较高的个体,对应较低的交叉概率pc和变异概率pm,以保护进入下一代;相反,适应度较低的个体,给予较高的pc和pm,加强其进化的能力。自适应计算式[7]如下

式中,fmax为群体中最大的适应度值;favg为每代个体的平均适应度值;f'为两个交叉个体中较大的适应度值;f为变异个体的适应度值。经多次试验,当pc1取 0.9、pc2取 0.6、pm1取 0.2、pm2取 0.05 时效果较好。
6)加速循环。经选择、交叉、变异可得到n个子代个体,取代父代个体,循环操作,构成标准遗传算法。在此基础上,通过步骤3)选择适应度最高的s个个体,提取变量的变化区间,取代原始变化区间。随着进化的进行,变化区间会朝着全局最优的方向不断缩小,加速搜索的过程。实际操作中,可以进行两次标准遗传算法,把2s个优秀个体的变量区间作为新的变量区间,进行加速遗传算法的进化。当变量区间小于某阀值时,取进化个体中的最佳个体作为AGA的搜索结果。
2.算法稳健性分析
加速遗传算法不断朝着全局最优的方向进化,变量的区间随着进化的进行不断缩小,对变化区间是否保留最优个体必须进行稳健性分析。根据遗传算法的收敛性定理[8]:保留最佳个体策略的遗传算法能收敛于最优解的概率为1,保证遗传算法全局收敛的基本策略是生成的群体的有效基因不缺失概率尽可能大,并通过合适的选择、杂交、变异操作把已发现的最优个体保存下来。加速遗传算法提取的2s个优秀个体的有效基因缺失的概率为

则2s个优秀个体包围最优点的概率为

变量个数为p,循环次数为q时,包围概率为

当p=3、s取20、q取20时,包围概率 P(n)趋近于1,可知加速遗传算法具有较强的全局收敛性,其保证了进化过程朝着全局最优的方向进行。
三、双差模糊度求解
GPS变形监测中,由于基线较短(一般小于15 km),采用双差观测值可大大消除卫星钟差、接收机钟差、对流层延迟和电离层延迟等误差。因此,双差模糊度有关系式

卫星到地面点的距离可表示为

式中,(xs,ys,zs)为卫星坐标;(xp,yp,zp)为地面点坐标。将式(9)展开则有

式中,p0为卫地近似距离。

四、实例验证
采用某超高层建筑物GPS变形监测数据对上述方法进行验证。外业观测采用Trimble R6双频接收机,采样率为15 s,卫星截止高度角15°,有效观测卫星6颗,取观测时间1 h的基线数据进行单历元解算。采用上期监测点坐标作为本次计算的初始坐标,利用 AGA 和 GA 对搜索区间[-0.2,0.2]、[-0.5,0.5]和[-1.0,1.0]的搜索效率进行了对比,表1列出了详细结果。

表1 不同变量区间的AGA与GA单历元解算结果比较(n=200,s=20)
由表1知,相同搜索区间的情况下,AGA的解算成功率和平均搜索时间都优于GA,这是因为AGA依据优秀个体的变化区间自适应地缩小变量的初始区间,降低了陷入局部最优解的可能性,从而提高了算法的搜索效率和解算成功率。两种算法在区间[-1.0,1.0]的成功率都不是很高,尤其是GA算法,成功率仅51.3%,究其原因是搜索区间不断增大,而种群规模n依然保持不变,群体多样性受到限制,算法的全局收敛性亦受到影响。此时,可以考虑增加种群规模来解决这个问题,相应的计算量和搜索时间也会增加。
为验证单历元解算方法的准确性,利用全部L1载波相位观测值进行静态解算,采用LAMBDA方法固定双差模糊度,作为该基线的基准值,图1显示了在区间[-0.2,0.2]情况下,AGA 单历元解算结果与基准值的偏差情况。
由图1知,大多数单历元解算结果和基准值的外符合精度都小于1 cm,少数历元Y方向偏差大于1 cm。由此可见,AGA单历元解算方法是正确的,解算结果是可靠的。从Y偏差和Z偏差还可以看出,历元间时相关性很强,存在系统误差的影响,如何有效地剔除单历元解算结果的系统误差,以便提取出监测点的真实变形,将是笔者下一步的研究方向。
五、结束语
AGA相比GA,其s个优秀个体可以反映模糊函数值在全局最优点附近各方向上的变化趋势,优秀个体的变化区间也就是全局最优点存在概率最大的区间,由此重新定义变量初始区间,能够快速、稳健地搜索到全局最优解,为双差模糊度的直接固定奠定了基础。
实际应用中,应尽量提供较高精度的监测点初始坐标,依据变形量的大小制定合理的变量搜索区间,并依据区间大小给定合理的遗传参数,以充分发挥加速遗传算法的搜索能力,保证GPS单历元的快速解算。受多路径效应等系统误差的影响,单历元解算结果存在强相关性,不能真实反映监测点的实际变形,如何剔除系统误差的影响,将是笔者下一步的研究方向。
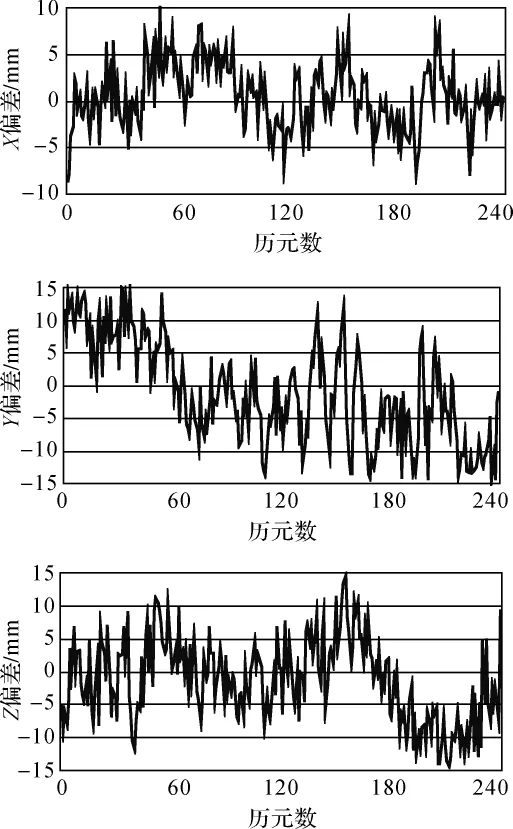
图1 单历元解算与静态解算比较
[1]张献州,熊永良,牟朝云.电视塔中心线垂直度及塔身扭转 GPS监测方法[J].测绘学院学报,2003,20(2):86-88.
[2]熊永良,黄丁发,张献州.一种可靠的含约束条件的GPS变形监测单历元求解算法[J].武汉大学学报,2001,26(1):51-57.
[3]刘智敏,刘经南,姜卫平,等.遗传算法解算GPS短基线整周模糊度的编码方法研究[J].武汉大学学报:信息科学版,2006,31(7):607-609.
[4]阳仁贵,欧吉坤,王振杰,等.用遗传算法搜索GPS单频单历元整周模糊度[J].武汉大学学报:信息科学版,2005,30(3):251-254.
[5]吴万清,宁龙梅,朱才连.一种单频单历元GPS整周模糊度的解算方法[J].武汉大学学报:信息科学版,2005,30(6):497-501.
[6]王新洲,花向红,邱蕾.GPS变形监测中整周模糊度解算的新方法[J].武汉大学学报:信息科学版,2007,32(1):24-26.
[7]王小平.遗传算法——理论、应用与软件实现[M].西安:西安交通大学出版社,2001:73-77.
[8]金菊良,杨晓华,丁晶.标准遗传算法的改进方案——加速遗传算法[J].系统工程理论与实践,2001(4):8-13.
