星载InSAR高程提取的误差因子分析
2013-12-11黄长军郭际明周命端喻小东袁长征
黄长军,郭际明,周命端,喻小东,袁长征
(1.武汉大学测绘学院,湖北 武汉430079;2.湖南城市学院市政与测绘工程学院,湖南益阳41300)
一、引 言
DEM的提取是InSAR数据处理的一项重要内容。在利用InSAR技术建立DEM的过程中,高程误差对DEM提取的精度起着重要的影响,其误差来源主要有几何误差和相位误差两个方面。本文根据斜距、基线、入射角、相位等因子与高程之间的几何构形及存在的函数关系,分析了影响InSAR测高精度因素的相关性及高程误差精度。
二、InSAR测高原理
InSAR观测的几何关系如图1所示。A1和A2分别表示主辅图像传感器;B为基线距;α为基线距与水平方向倾角;θ为主图像入射角;H为主传感器相对地面高度;P为地面目标点,其高程为h。地面点P到天线A1的斜距为R,到天线A2的斜距为R+ΔR。为讨论方便,假设主从相对获取期间无地表形变,且无大气影响[1-2]。
由图1可得,P点的高程

根据余弦定理可得
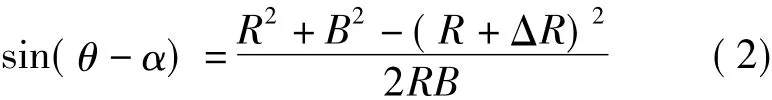
将式(2)忽略(ΔR)2项,得到
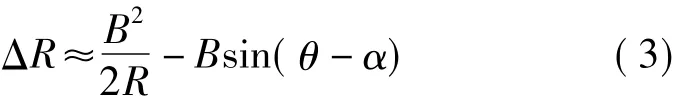
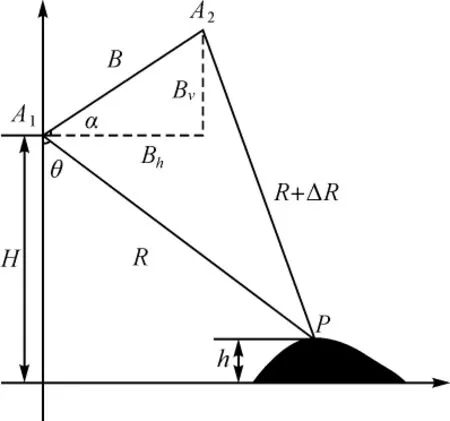
图1 基线沿水平向分解关系
在星载系统中,由于B2=R,为此,进一步忽略,可由式(3)得到
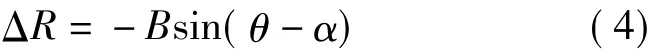
根据式(1)~式(4),利用卫星高度H、基线B、基线倾角α及斜距差ΔR,可确定高程,即
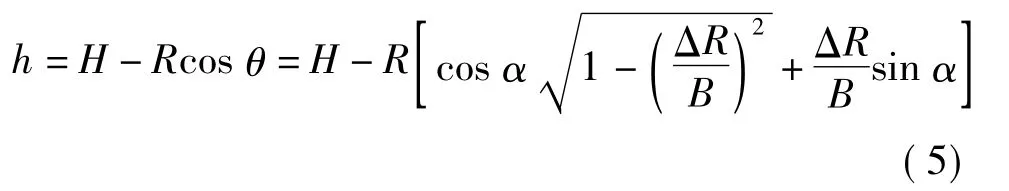
三、基线分解及高程精度分析
1.分解原理
如果将基线沿水平方向分解成Bv和Bh(如图1所示),则Bv和Bh分别表示基线的垂直分量和水平分量,则将式(2)展开后忽略掉(ΔR)2项,得[3]
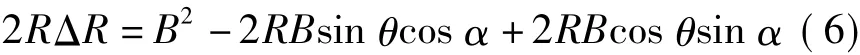
两边同时除去2R,得到
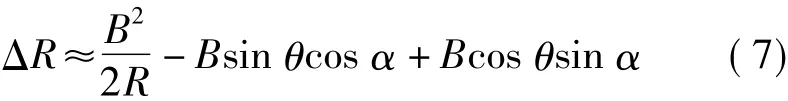
在星载系统中,由于B2=R,为此,进一步忽略,可由式(12)得到
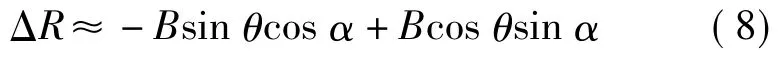
又由图2可知,有
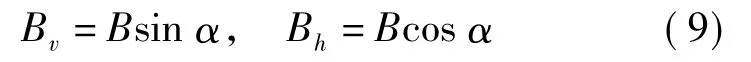
则在两次飞行过程中,星载SAR天线与同一地面单元的斜距差ΔR可近似为
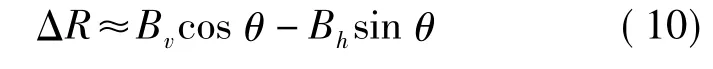
将式(10)代入式(5)得到
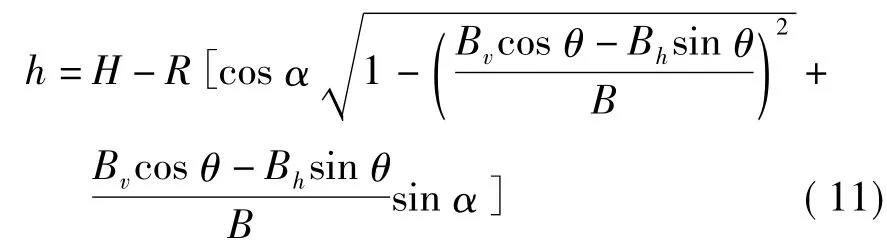
2.精度分析
根据波长、相位、距离和时间的关系,得两次飞行在同一地面分辨单元回波信号的相位差与斜距差的关系为
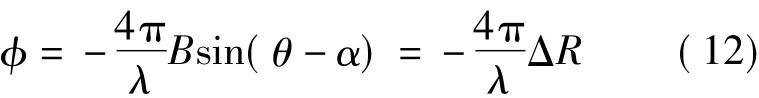
对式(11)、式(12)进行全微分,整理可得
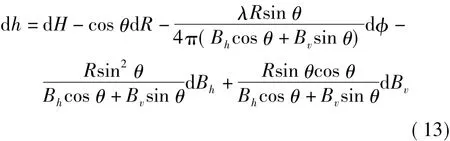
根据协方差传播定律,如果这些量的误差之间互不影响,则得到高程误差公式

事实上,斜距、基线、相位及高度等量的误差之间不可能相互独立,在进行高程的提取过程中,它们之间有影响关系,其影响的关系式在文献[4]已经给出,这里不再赘述。
四、相关误差因子分析
由式(14)可知,高程精度与传感器的高度、斜距、基线倾角、相位测量误差、基线长度有着紧密的关系[5]。σH是由于InSAR距地球表面的径向距离的不确定性而引起的测高误差,这个误差源在仅要求相对高度测量时并不重要,可以将其校正掉。影响InSAR高程精度的误差因子关系如下:
1)高程精度与相位测量误差的关系为
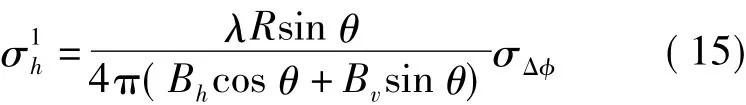
σφ是由于相位φ的不确定性引起的测高误差。在干涉测量中,相位误差是引起高度不确定度的一个主要因素[6]。系统噪声、斑点噪声、多视数、配准误差、时间的去相关和基线去相关等是相位误差的主要来源。其中,热噪声对于相位测量的影响是不容忽视的。由于SAR的特点,干涉测量中的每一个像元或多或少都要受到斑点噪声或衰落噪声的影响,常用方法一般是采用多个像元,即多视平均法来消弱和减少上述噪声的影响。因此,多视处理会影响到相位的测量精度[6]。在配准方面,干涉图的相位反映的是两幅图像的同一目标像元之间的相位差,如果两个像元之间不能准确地配准或配准失败,干涉图中的散射体成分会引起相位的测量误差[4]。
利用文献[7]给出的 R=850 km,θ=21°,得到相位误差、基线长度、基线倾角和高程精度的误差曲线。图2~图3显示了在不同基线的条件下,相位误差传播系数、基线误差传播系数及基线倾角误差之间的影响关系。从图2~图3中可知,随着基线长度的增大,相位误差传播系数会逐渐减少;就整体而言,在倾角越大和基线长度越短的情况下,基线长度误差对高程测量误差的影响就越大,短基线对倾角的变化反而比较敏感;反之,随着倾角的变化,基线越长则测高精度就越高。
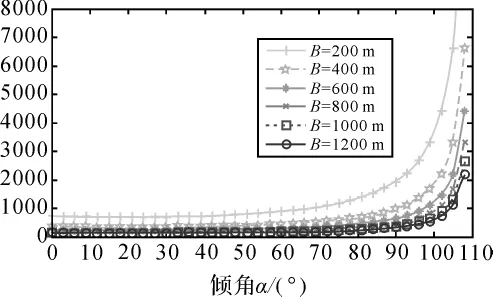
图2 相位误差传播曲线
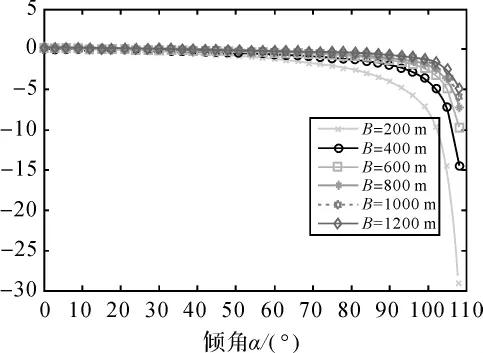
图3 基线误差传播曲线
2)高程精度与基线长度的关系为
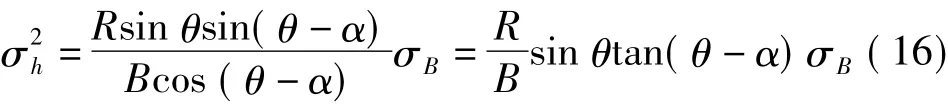
σB是基线误差系数,是由于基线的不确定性引起的,它与载体的姿态和基线长度的不确定性有关。由图3可知,随基线长度的增大,基线误差传播系数逐渐减少。由于斜距误差的精度受到测量地形、大气延迟、地球曲率、相位测量等误差的影响,在星载INSAR测量中,在保证干涉相干的情况下,宜选取较长基线的影像对来进行干涉处理[8]。但应该注意的是,并不是基线越长越好,基线长度受到实际情况的制约,应根据实际情况来选定合适的基线。
3)高程精度与基线倾角的关系为

4)高程精度与斜距的关系为

σR是由于斜距 R的不确定性引起的测高误差,除了与视角θ有关外,还与SAR的定时系统的不定性、采样时钟的抖动和电波通过大气及电离层的延时等因素有关[5]。对于大气及电离层的延时因素,由于在电波传播的路径上水汽的分布并不均匀,很难用简单方法进行高精度的校正,这成为现在研究的一个热点[9]。从图4可知,随着入射角的增大,倾角和斜距对高程的影响是相反的。
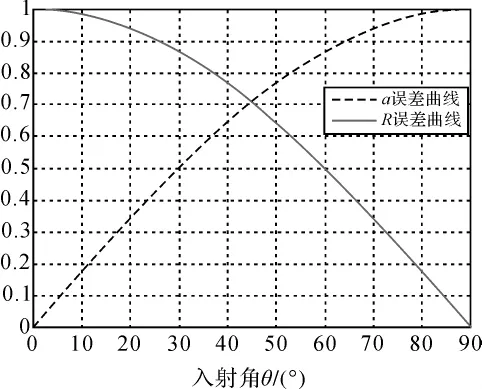
图4 R误差与α误差传播曲线
5)高程精度与Bh的关系为
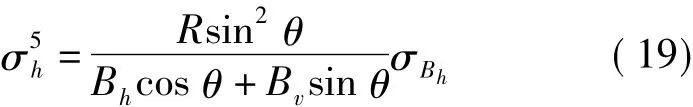
6)高程精度与Bv的关系为
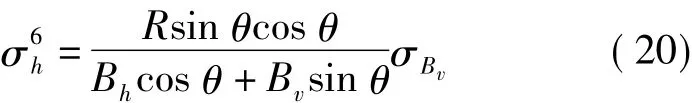
σBh、σBh是由于基线的不定性引起的误差,与载体的姿态和基线长度的不定性有关,利用文献[7]中的 R=850 km,分别取 θ=23°、30°、33°和51°,α∈[0°,350°],做出 Bh参数与测高精度的误差曲线(Bv误差曲线图与Bh相似,限于篇幅,没有列出),其关系如图5~图8所示。
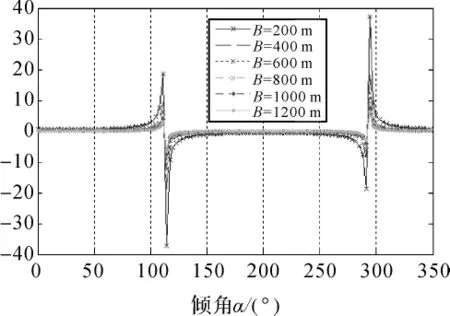
图5 Bh误差传播曲线(θ=23°)
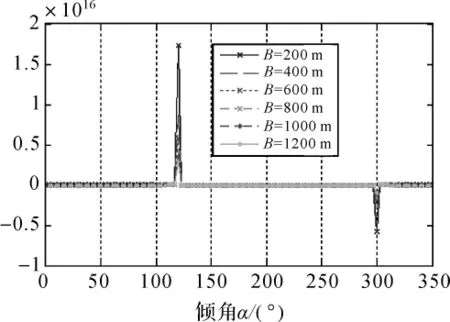
图6 Bh误差传播曲线(θ=30°)
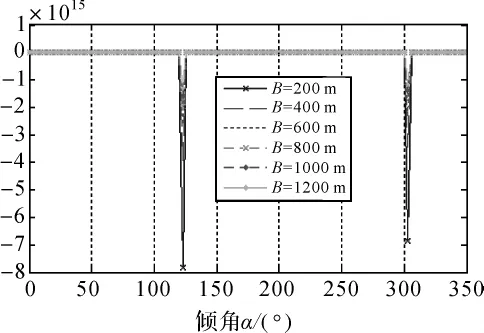
图7 Bh误差传播曲线(θ=33°)
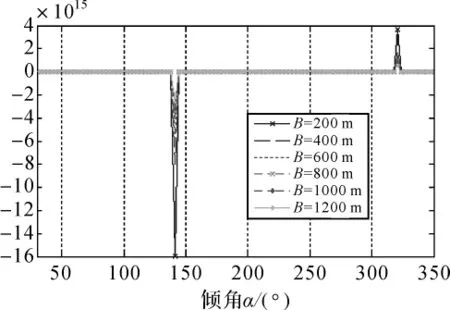
图8 Bh误差传播曲线(θ=51°)
由图5~图8变化曲线可知,基线分量Bh是随着θ逐渐增大,基线倾角α将逐渐减小来对高程精度影响的。基线倾角对高程精度的影响规律是基线长度越短,θ-α=|π/2|时,基线长度误差对高程的影响越大。而且基线短,其对倾角的变化比较敏感,反之基线越长测高精度越高。随倾角的变化,精度变化趋势则不是很明显。以图7为例,当B=200 m时,高程精度影响从0迅速下降到-8×1015,由此可见波动影响是很大的。
图9所示为σBh、σBv与σh分量之间的相对误差系数关系。由图9可知,要使基线分量与高程的相对误差为0.4 m的绝对误差,需要基线的相对测量误差分别为1.76 ×10-3和 2.97 ×10-3。就上述误差的特性来看,涉及的误差具有公共误差的属性,若要使测量高程精度达到符合精度要求,准确确定干涉基线就显得非常必要[6]。
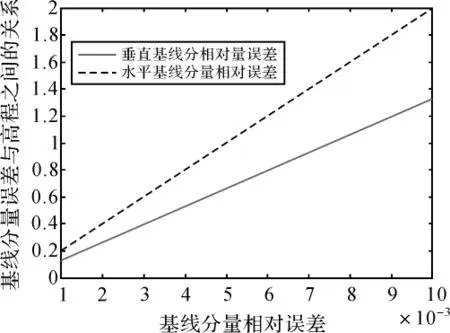
图9 σBh、σBv与基线相对测量误差的关系
根据干涉测量的特性,可以在干涉测量区域设置一些具有精确地形信息的特征点或地面控制点作为参考基准,然后利用成像区域内的特征点或控制点信息,获取实际的基线信息和基线姿态。特征点或控制点最好是选择一些已知位置和高度的强反射点,如裸露的岩石、房角或人工角反射器等,选择的特征点或控制点不得少于3个。利用已知控制点高度的公式反算出基线信息,利用这个方法把测高误差近似减小到仅由相位测量误差引起的数值,从而使基线估计的误差减小到可以接受的程度。
由式(14),令 Bhcosθ+Bvsinθ=0,结合式(9)得到
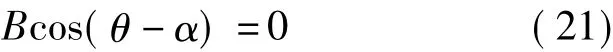
由式(21)可知,当θ-α=π/2时,Bhcosθ+Bvsinθ的误差系失去意义[8]。此时相位和基线对高程测量精度的影响为0。在处理干涉影像时,这种情况应引起特别的重视,利用这个特点可以合理选择干涉影像。
五、结束语
本文推导了星载InSAR测高精度与斜距差、基线等成像参数之间的关系,并对影响测高精度的相关误差因子进行了分析。结果显示,基线参数(基线长度和基线倾角)是影响高程精度的一个重要因素。随着基线长度的增大,相位误差传播系数会逐渐减少;就整体而言,在倾角越大和基线长度越短的情况下,基线长度误差对高程测量误差的影响就越大,短基线对倾角的变化反而比较敏感;反之,随着倾角的变化,基线越长则测高精度就越高。最后通过对水平基线和垂直基线对测高精度的影响分析,证明了在获取高精度的地面高程过程中,基线参数的估算精度至关重要。要准确确定干涉基线,可以采用地面控制点作为参考基准,通过求控制点高度的公式反算出基线来减小基线估计的误差,以此减小基线误差给测高误差带来的影响。
[1]王超,张红,刘智.星载合成孔径雷达干涉测量[M].北京:科学出版社,2002.
[2]袁孝康.干涉式合成孔径雷达的测高精度分析[J].空间电子技术,1999(2):22-29.
[3]ZEBKER H A,GOLDSTEIN R M.Topographic Mapping from Interferometric Synthetic Aperture Radar Observations[J].Journal of Geophysical Research,1986(91):4993-4999.
[4]刘国林,郝晓光,薛怀平,等.影响InSAR测高精度因素的相关性分析[J].武汉大学学报:信息科学版,2007,32(1):55-58.
[5]LYONS S N.Investigations of Fault Creep in Southern California Using Interferometric Synthetic Aperture Radar and GPS[D].San Diego:University of California,2002.
[6]袁孝康.干涉式合成孔径雷达测量技术[J].上海航天,1998(5):20-26.
[7]HANSSEN R F.Radar Interferometry:Data Interpretation and Error Analysis[M].Netherlands:Kluwer Academic Publishers,2001.
[8]邓永和.InSAR测高精度的精密公式[J].大地测量与地球动力学,2010,30(1):92-94.
[9]JOUGHIN I.Estimation of Ice2Sheet Topography and Motion Using Interferometric Synthetic Aperture Radar[D].Washington:University of Washington,1995.
[10]张磊,伍吉仓,陈艳玲.InSAR高程模型及其精度分析[J].武汉大学学报:信息科学版,2007,32(2):108-111.
