基于施引期刊的科技论文学术影响力的多属性描述研究

●郭 强，赵 瑾

（1．郑州大学 信息管理系，郑州 450001；2．中国人民解放军陆军军官学院 军事运筹教研室，合肥230031）

由于被引次数与文献的学术价值之间具有较为普遍的相关性，所以，可以选取被引次数来反映论文或者是期刊的学术重要性以及学术影响力。而且被引次数能够对文献被引情况的统计性质进行大致的表征，能够满足指标的可测取性要求以对文献的学术价值进行度量，因此，可将基于被引次数的相关复合指标以及论文的下载次数纳入到论文学术影响力的多属性描述中以满足指标的全面性要求。需要指出的是，利用被引次数来对论文的学术影响力进行衡量是建立在论文被引次数的绝对量的基础上，因为论文被不同期刊引用并不存在对论文影响力表征上的差异，但是不同的施引期刊对论文影响力的体现会有所不同，如论文被具有高影响力的期刊引用所获得的影响力可能会更高一些。因此，本文希望在论文影响力的多属性描述中对施引期刊的差异进行体现，并对论文影响力分值的分布情况进行考察以检验多属性描述的合理性，而且希望对建立在论文被引次数基础上的复合指标进行考察，从而探讨影响力指标及其多属性应用对施引期刊之间差异表示的适用性。

1 相关性考察

在对期刊的学术影响力进行评价时，被引次数与影响力之间的相关性使得期刊被引次数的绝对量能够成为较为基本的描述指标，而且由于施引期刊的不同能带来的对被引期刊影响力表征上的差异，［1］因此，需要在被引次数绝对量的基础上对施引期刊的重要性或是影响力之间的不同进行体现。那么与期刊相类似，由于论文的影响力与其施引期刊的影响力之间具有一定的相关性，所以，在被引次数中考虑施引期刊的不同，能够有助于区分具有相同被引次数的论文对其影响力的描述。

为进一步论证论文影响力与其施引期刊影响力之间的相关性，选取2004年6月份至2005年6月份出版的图书情报类期刊论文作为考察对象，根据所得数据对论文的影响力指标进行主成分分析，由此对指标的权重进行确定并得到每篇论文的影响力分值，其中利用文献［2］中的论文影响力指标体系考虑论文的下载情况，选取CNKI的镜像站版作为数据的来源，数据的统计时间为2011年10月。如果以施引期刊的影响因子的算术平均值来近似表示论文的施引期刊的影响力，其中施引期刊相同时对期刊的影响因子进行累计求和，那么，每篇论文均有与其相对应的影响力分值以及施引期刊影响因子的平均值，从而针对这两个变量的样本对能够得到该两变量之间的等级相关系数为0.488，同时对两变量之间的相关关系进行显著性检验，能够得到在0.01水平下两个变量之间在总体上具有等级相关性。采用等级相关系数的原因是由于论文的影响力分值与其施引期刊影响因子的平均值在论文中可能均不严格服从正态分布。

在对各指标值进行均值化的基础上得到，在总方差解释表中，前两个主成分所对应的相关矩阵的特征值分别为7.827与1.598，并且这两个主成分的方差累积百分比能够达到85.682%，各指标的公因子方差的平均值为0.857且标准差为0.110，所以提取前两个主成分，由主成分所对应的特征值以及各指标与主成分之间的相关系数能够得到主成分与各指标之间的线性关系，以及论文影响力的分值表达式，分值表达式中的指标值取均值化后的指标值。由于在这里是利用施引期刊影响因子的平均值来对论文的施引期刊的影响力进行表征，所以需要对施引期刊的影响因子进行求和，因此，选取单一学科领域的期刊论文作为考察对象以进行施引期刊影响力之间的近似比较。需要指出的是，对施引情况的影响力进行平均时，没有将论文被学位论文引用的情形包含在施引范围内，是原因如果需要对论文影响力的描述较为全面时，则需要将论文被学位论文引用的情形纳入到施引范围内，这样会对论文的影响力分值与其施引情况影响力之间的样本相关系数产生影响，这也是造成上述等级相关系数偏低的原因。另外，还需对利用样本的平均值作为特征对考察的有效性进行探讨，如选取施引期刊影响因子的最大值来对论文的施引期刊的影响力进行近似地表示，那么能够得到论文的影响力分值与该指标之间的等级相关系数为0.714，类似地能够对这两个变量之间的等级相关性进行显著性检验，可以得出在0.01水平下，这两个变量在总体上具有等级相关性。

此外，还可以利用施引期刊影响力的不同，对具有相同或相近被引次数的论文的影响力进行描述，从而有助于体现该类论文影响力的差异，如将所选取的论文按照被引次数降序排列并进行分组（各分组的论文数量大于7，共29个分组），假设相同分组内的论文具有相近的被引次数，那么可以得到各个论文分组中每篇论文的影响力分值以及施引期刊的影响因子平均值，由此可以得到这两个变量的样本相关系数，以及相关系数的平均值0.334，标准差为0.196，并且在0.01水平下有13个分组的论文影响力分值与其施引期刊的影响力之间在总体上具有等级相关性。同样，由于学位论文的影响力与期刊影响力之间的可加性，所以在论文的施引情况中没有将学位论文的施引情形包含在内，同时在对论文的施引期刊的影响力进行描述时，选取了施引期刊的影响因子的平均值来进行表示，这是造成相关系数平均值偏低的原因，而且，学位论文的施引情形在各论文分组中分布的随机性也会使得相关系数具有较大的标准差。为了考察施引期刊的影响力表征，选取施引期刊影响因子的最大值来进行表示，可以得到各个分组中相关系数的平均值仅为0.260，标准差为0.164，其中分组情况保持不变，在该情形下，尽管各个分组中的相关系数的最大值能够达到0.670，但是相关系数也会出现负相关的情形，如最小值为-0.351，并且在0.01水平下仅有3个分组的论文影响力与施引期刊的影响力之间在总体上具有等级相关性，同时在负相关情形的分组中，这两个变量在总体上也均不具有负的等级相关性。这说明如果施引期刊具有较高的影响力，对于论文的影响力也会具有促进作用，所以影响因子的最大值与论文的影响力分值之间会具有其正相关性。另外，选取影响因子的最大值作为施引期刊影响力的表征时，两个变量之间的相关性相对较低，相关系数表现为较小的平均值以及较大的标准差，究其原因是由于采用施引期刊影响因子的最大值对施引期刊的影响力进行反映的全面性，采用影响因子的最大值能够对施引期刊的影响力的大小范围进行大致的表示，论文施引情况的引用数量以及施引期刊影响力的大小都要进行考虑。此外还需要对施引期刊的影响力表征进行考察，从而对于被引次数相同或相近的论文，能够对论文的影响力分值与施引期刊的影响力之间的相关程度进行有效的体现，由此能够从侧面检验利用施引期刊的不同来对具有相同被引次数论文的影响力差异进行反映的有效性。

由以上考察可显示，在分组的情况下，各分组的论文的影响力与其施引期刊的影响力之间具有一定的正相关性，如果这种相关性成立，那么会使得引入施引期刊的影响力来对论文影响力进行反映具有其实际基础，而且上述考察结果所显示的弱相关性也从侧面意味着需要引入其他指标来满足描述的全面性。

如果论文的影响力与施引期刊的影响力之间存在较好的正相关性，其中论文影响力是建立在影响力指标体系的基础上，论文被引次数的绝对量是其中的组成部分，那么在该体系中去除论文被引次数绝对量之外的与论文被引情况有关的指标，包括论文的年均被引次数，论文在发表后三年中的被引次数，论文在发表后的最大年度被引量，论文的相对年均被引量，以及论文在发表后三年中的相对被引总量，能够得到分别建立在调整前后的描述体系上的论文影响力之间会具有较高的相关性，及被引类指标之间的相关系数均相对较高且最小值为0.922，所以调整后的论文影响力与施引期刊的影响力之间也会具有较好的正相关性。那么在假设剩余各指标相互之间存在一定独立性的基础上，假设由被引次数的绝对量所体现的论文影响力与施引期刊的影响力之间会存在正相关性，从而可以在两者之间建立线性回归关系。由于施引期刊的影响力表征的理想情况是将施引期刊影响力的大小以及施引的数量均纳入在内，所以当施引期刊的影响力表征为零时，由被引次数的绝对量所体现的论文影响力也会为零，由此，可以认为该两变量之间线性关系为正比例关系，设比例系数为r。那么，对于被引次数为1的论文，其被引数的绝对量所表示的论文影响力应当等于r乘以施引期刊的影响力，所以对于被引次数为n的论文，其被引次数的绝对量所表示的论文影响力能够等于各个单位被引次数所表示的论文影响力之和，从而等于r乘以n份施引期刊的影响力之和。如果以施引期刊的影响力之和来表示论文施引期刊的整体影响力，那么，施引期刊的影响力之和与其平均值之间的等级相关系数近似为0.735，并且在0.01水平下施引期刊的影响因子之和与影响因子的平均值在总体上具有等级相关性，被引次数绝对量所表示的论文影响力与施引期刊的影响力之间为正相关相一致，另外，在对论文的影响力指标进行主成分分析时，如果对指标采取均值化，那么某一指标所乘常系数r的变化不会影响指标均值化后的取值；同时该系数r的变化也不会改变指标之间的相关系数矩阵，所以可以取比例系数r等于1，由此，能够得到由被引次数的绝对量所表示的论文影响力等于各施引期刊的影响因子之和，进一步地，能够对影响力指标进行主成分分析并对各指标的权重进行确定。

2 影响力描述

除了将各施引期刊的影响因子之和作为指标之外，仍然选取文献［2］中的论文影响力指标，包括论文所属期刊的影响因子，论文所属期刊的相对影响因子，论文的下载次数，论文的年均下载次数，以及论文的相对年均下载次数，其中相对指标值仍然是利用绝对指标值与该绝对指标值的平均值进行相除来得到。对所选取的论文样本，在对各指标进行均值化的基础上能够得到指标的相关系数矩阵。在该矩阵中论文所属期刊的影响因子与其相对影响因子之间的样本相关系数属于强相关，并且这两个变量与其余变量之间的样本相关系数的最大值仅为0.362，而其余变量之间的相关系数的最小值却能够达到0.553，由此按照指标之间的相关系数可以对指标进行归类，并且能够提取两个主成分来对这些指标进行总体的反映，这两个主成分分别与期刊类指标以及论文类指标相对应。在总方差解释表中，前两个主成分的方差累计百分比能够达到90.545%，对应的相关系数矩阵的特征值分别为3.698以及1.734，如果选取这两个主成分，那么利用成分矩阵中各变量与主成分之间的相关系数能够得到变量的公因子方差分别为0.533、0.989、0.989、0.981、0.966、0.973，同时公因子方差的平均值以及标准差为0.905与0.182，所以能够选取前两个主成分来对指标进行描述。在成分矩阵中，施引期刊影响因子之和与第一主成分的相关系数为0.729，其余的论文类指标与该主成分的相关系数均在0.9以上并且最大值为0.931，相对应地，与第一主成分相比，两个期刊类指标与第二主成分之间具有相对较高的相关系数且均为0.834，于是所选取的两个主成分能够分别与论文类指标与期刊类指标相对应，但是，当选取这两个主成分时，施引期刊的影响因子之和具有相对偏低的公因子方差，所以考虑选取前三个主成分，此时方差累计百分比为99.642%，各个变量的公因子方差的平均值等于0.996，而标准差仅为0.005，且与第三主成分相对应的特征值为0.546，在成分矩阵中，除了施引期刊影响因子的求和之外，其余指标之间的结构关系与选取两个主成分时的情形相同，论文的下载类指标与第一主成分之间的相关系数相对较高并且均在0.920以上，期刊类指标与第二主成分之间的相关系数均为0.834，而施引期刊影响因子之和与第一以及第三主成分之间的相关系数分别为0.729与0.683。由于这两个相关系数的差异相对较小，所以对于该指标与各个主成分之间的对应关系还需要做进一步的讨论。施引期刊的影响因子之和能够与论文的被引类指标相对应，或者是与上述的论文下载类指标以及期刊类指标不同，而将该指标归为第三类，从而第三主成分能够与论文的被引类指标相对应，如果不强调对论文类指标的划分，那么仍然是选取前两个主成分，这两个主成分分别对应于论文的论文类指标以及论文的期刊类指标，由此，根据各指标与主成分之间的相关系数以及与主成分对应的特征值，能够给出主成分表达式为F1=0.379z1+0.282z2+0.282z3+0.484z4+0.479z5+0.484z6以及F2=0.034z1+0.634z2+0.634z3-0.256z4-0.262z5-0.248z6，同时论文的影响力分值为w=0.269z1+0.394z2+0.394z3+0.248z4+0.242z5+0.250z6，其中 zi为各指标均值化后的取值。

进一步对所得影响力分值在论文中的分布情况进行考察。将论文按照其影响力分值进行降序排列，并分别对论文数以及相应的影响力分值求累计和，可以得到论文的累计量与论文影响力的累计分值之间的关系（如图1所示），其中假设所选取的论文样本能够满足相同考察时段的要求。

图1 论文累计量与论文影响力分值累计量的关系图

在图1中，横轴为论文累计数的对数，纵轴为论文影响力分值的累计量，从直观上论文的影响力分值在论文中具有一定的布拉德福分布的特征。如果取分区数为3，那么相应地能够取核心区的论文数为291，各分区影响力分值累计和的平均值为1092.576，标准差为0.557，此时各分区论文累计和之间相继比的平均值为2.440，标准差偏大为1.241。如果对分区数进行调整取为5，那么相应的有核心区的论文数为144，各个分区的论文累计和的相继比的平均值为1.486，标准差仅为0.144，同时各个分区的影响力分值的平均值为655.546，标准差仅为1.087。由此可以认为，该分布能够在一定程度上满足布拉德福分布分区的要求。另外，尽管并不明显，但是在论文影响力分值偏低处可以看到格鲁斯下垂的出现，这意味着在影响力偏低的区域有相对较多的论文具有偏小的影响力分值，从而使得当论文的累计量增加时，论文影响力分值的累计和的增长速率会有所下降，造成该现象不明显的一种可能原因是在这里选用了论文的下载情况来对论文的影响力进行描述。与被引次数较高的论文相比，网络环境对被引次数相对较低的论文的影响力的提升幅度会相对较高，这样会使得论文影响力分值在论文中的分布更为分散，而这种分散性对于末尾分区中大量论文具有偏低影响力分值的现象会有一定的抑制作用。如果选取分区数等于5，那么核心区与非核心区的拟合方程分别为m=12.535n0.802以及m=1163.3Lnn-5538.6，其中判定系数分别能够达到0.9989以及0.983，m和n分别为论文影响力分值的累计和以及论文数的累计和，那么，在总体上，论文累计和与其影响力分值累计和之间的关系能够在一定程度上与布拉德福分布的要求相一致。

另一方面，尽管考虑施引期刊的不同，会使得论文的影响力分值与相应的排序情况发生变化，但是与被引次数偏低的论文相比，被引次数相对较高的论文影响力的变化幅度会相对较小。

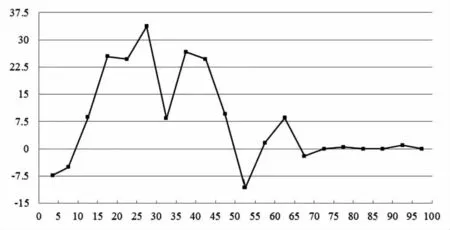
图2 论文被引次数与论文影响力排序变化情况的关系图

将论文按照其被引次数进行降序排列，对于每篇论文能够分别得到在考虑施引期刊差异以及只考虑论文被引次数绝对量情况下的影响力分值与相应的影响力排序，以及两种情况中论文影响力排序值的差值（如图2所示）。在图2中，横轴为论文的被引次数，纵轴为被引次数范围中论文排序值差值的平均值。由图2可以看出，在总体上随着论文被引次数的降低，论文影响力排序的变化幅度也会逐渐增大，同时在被引次数相对居中的区域，随着被引次数的较少，论文影响力排序值的差值会逐渐增大并且大于零，进而在被引次数相对偏低的区域，影响力排序值的差值会逐渐减小并且最终为负数。由于在被引次数偏高的区域，论文影响力的排序情况没有发生显著的变化，所以在考虑施引期刊的不同时，被引次数偏低以及居中的论文的影响力排序会发生相互之间的转化，并且在总体上被引次数相对居中的论文的排序值会有所上升，同时具有偏低被引次数的论文的排序值也会相应地有所下降。这意味着对于所选取的论文样本，当引入施引期刊的差异时，在被引次数居中的区域，施引期刊影响因子之和对于论文排序的降低效应大于对排序的提升效应；而且，在被引次数相对较高的区域，影响因子之和对于排序的降低与提升效应均相对较小。另外，在被引次数相对较低的区域，与论文的被引次数相比，施引期刊的影响因子之和会表现为对论文的排序具有提升作用。由于在被引次数偏低的区域，相对较多的论文具有相对较低的影响力分值，所以，施引期刊的差异对于论文影响力分值的排序情况具有相对较大的影响，这也是在被引次数偏低区域影响力排序值变化幅度相对较大的另一个原因。

3 结束语

需要指出的是，如果论文的影响力是建立在调整之前的描述体系上，由于论文影响力与施引期刊的影响力之间会存在一定的正相关性，而且调整之前的描述体系所包含的被引次数的相对量与最大年度被引量等指标与施引期刊的影响力会有关联，那么此时，仅由被引次数的绝对量体现的论文影响力与施引期刊的影响力之间的线性回归关系并不显然。利用调整后的描述体系，能够近似地认为两者之间具有正相关性，并在此基础上进一步将其余的最大年度被引次数等被引类指标纳入进来。

［1］任胜利.特征因子:基于引证网络分析期刊和论文的重要性［J］.中国科技期刊研究，2009，20（3） :415－418.

［2］金晶,等.不同学科领域自然科学论文学术影响力评价与比较的可行性研究［J］．科技管理研究，2010（14）：279－284.