迫击炮弹弹道一致性检验与设计探讨*

黄成辉，蒋东方，赵星海

(国营9613厂，湖南永州 425000)

0 引言

同一火炮配用多种不同的弹药，要求通用射表或弹道一致，这是外弹道设计中经常碰到的问题。关于弹道一致性检验方法、判据以及枪弹、舰炮等武器系统的弹道一致性研究甚多。而迫击炮弹飞行轨迹呈抛物线形，近似于真空弹道，外弹道相对简单，国内外鲜有系统、专一的研究。文中基于弹箭弹道一致性检验原理和方法，试图探讨一条适合于迫击炮弹弹道一致性检验与设计控制的途径。

1 检验原理和方法[1]

1.1 检验原理

同一火炮同一射击条件下射击同一弹种的弹着点散布服从正态分布，射击不同弹种的正态分布存在差异。按照数理统计的观点，判断弹道是否一致，就是判断两弹种是否属于同一母体，检验其正态分布的数学期望是否存在显著性差异。

设在地面坐标系o-xyz中(见图1)，对比弹和被试弹的弹着点坐标分别为(x0，z0)、(x1，z1)。假设检验成立，则认为两弹弹道一致。式中E系射程或方向概率误差。

图1 地面坐标系

1.2 检验和试验方法

弹道一致性检验方法分为成组检验法和成对交叉检验法两种。在实际工作中，都是采用成对交叉检验法，即在同一火炮相同射击诸元下，采用对比弹与被试弹单发交叉射击，成对统计弹道差，用t检验检验其平均值，评定其弹道一致性。

迫击炮射角为45°～85°，发射装药属于变装药，其弹道一致性检验试验一般选取3个装药号(最大、最小和中间某装药号)，每个装药号以2～3个射角(最大、最小和中间某射角)射击被试弹和对比弹各1 ～3组，每组7 ～ 10发[2]。

2 理论设计方法

弹道一致性设计就是控制被试弹与对比弹的弹道差小于一致性设计控制限，保证被试弹以一定接收概率通过样本试验检验。一致性设计控制限依赖于一致性界限、概率误差和一致性接收概率等，是两弹设计弹道差的允许极限。一致性界限由试验组数、发数及显著性水平和概率误差确定，是试验检验评定弹道一致性的极限判定值。

2.1 试验组数m、每组试验发数n以及显著性水平α 的选取[3]

就迫击炮弹而言，一般取m=3、n=7。研制前期，因方案多变，一般取m=1、n=7。当要求平均弹道基本一致时，取α=0.01;当要求平均弹道一致时，取 α =0.05。

2.2 一致性界限系数λs[3]

一致性界限系数λs是一致性界限a与概率误差E的比值，按文献[3]相关公式解出，计算结果见表1。

2.3 一致性设计控制限系数λsp[3]

一致性设计控制限系数λsp是弹道一致性设计控制限K与概率误差E的比值，按文献[3]相关公式解出，计算结果见表1。

表1 常用 λs、λsp值

2.4 一致性设计控制限K

一致性设计控制限K[3]由下式确定:

2.5 计算弹道差Δ

首先，校核被试弹的飞行稳定性，应符合要求。然后，应用射表，或利用外弹道计算程序、自身阻力系数计算，求出对比弹在不同飞行速度时的阻力系数(或弹形系数)。再估算被试弹的阻力系数(或弹形系数)，应用外弹道计算程序求出其射程。最后，计算两弹在相同初速、射角下的弹道差Δ。

2.6 结果评定

若Δ≤K，则认为两弹弹道一致。

3 设计实例

以某型尾翼式82mm迫击炮新弹设计为例，介绍迫击炮弹弹道一致性的设计和检验过程。82mm新弹(被试弹)与82mm制式弹(对比弹)的外形分别见图2、图3，指标要求其母弹平均弹道基本一致。

图2 新弹外形图

图3 对比弹外形图

新弹内部结构与对比弹差异显著，弹体外形也有所不同。对比弹为整体式圆柱部，新弹圆柱部由三段组合而成，长度有所增加，对外弹道性能影响较大。为了减少膛内及炮口初始扰动，提高精度，新弹弹头与前定心部之间设计采用了类似于火箭弹的圆柱部连接方式。

设计时，首先确保新弹的设计膛压、初速、膛内药室容积与对比弹相同，弹重在对比弹弹重分级范围内，配用对比弹的发射装药，即保证内弹道一致。其次，在优先保证弹丸装填、终点效应和最大地面射程及密集度等前提下，力求两弹几何外形、尾翼稳定装置、弹重、质心和赤道转动惯量等弹丸特征数基本一致，尽量消除影响弹道一致性的不利因素，或减轻其影响程度。

3.1 判断新弹的飞行稳定性[4]

根据弹丸设计理论，应用特征数计算程序、АНИИ法等，求出有关参数:赤道转动惯量 Jy=0.0630kg·m2，摆动波长λ =46.5m，静态稳定储备量B=16.40%。根据稳定性判定准则，因为静态稳定储备量B介于15% ～20% 之间，且将点(lgJy，λ)画在现有迫击炮弹飞行稳定性曲线图上，该点处于稳定区域内，表明新弹飞行稳定性满足要求。

3.2 计算对比弹的标准射程

依据射表(或实测值、弹丸自身阻力系数)，求得对比弹各装药号不同射角的标准射程，见表2，自身阻力系数值见表3、图4。

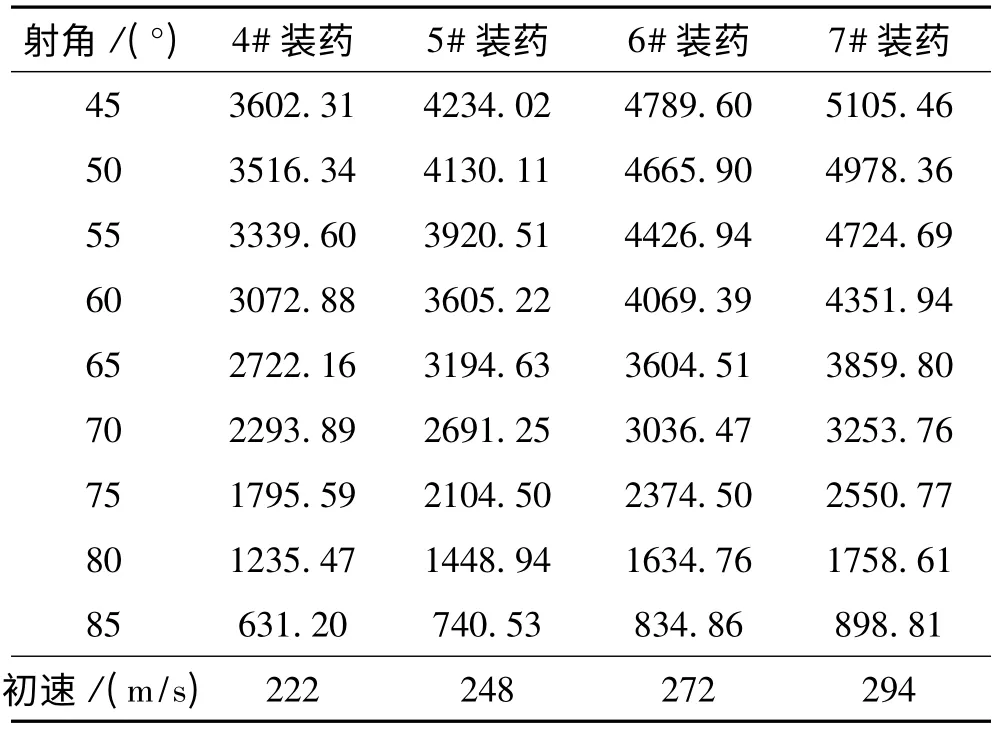
表2 对比弹标准射程 m

表3 对比弹自身阻力系数Cx0(M)

图4 对比自身阻力系数Cx0(M)曲线

3.3 推算对比弹的等效弹形系数

依据表2，按照文献[4]外弹道计算程序，进行符合性计算，可反向推算出对比弹对应于43年阻力定律的弹形系数，即等效弹形系数，见表4。根据实践经验，引入等效弹形系数概念，可以简化计算，对于迫击炮弹的设计计算符合性较好。

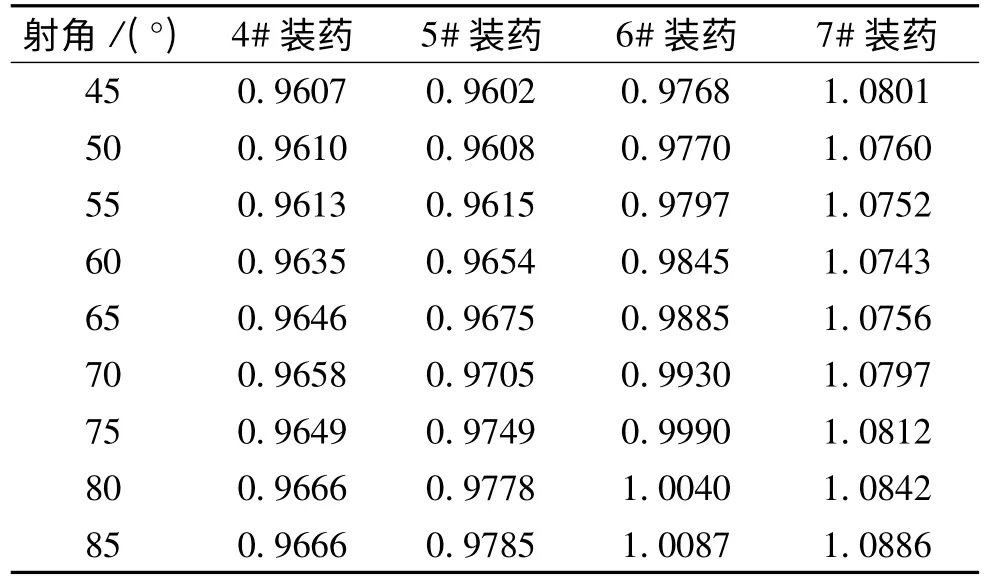
表4 对比弹的等效弹形系数i'43d

3.4 计算一致性设计控制限

对比弹有4个发射装药号(4#～7#)，现选取4#、7#装药进行计算。根据历史试验数据，统计得到对比弹射程和方向的概率误差Ex、Ez，见表5。绘制E － θ曲线(描述概率误差随射角变化的趋势)，见图5、图6。

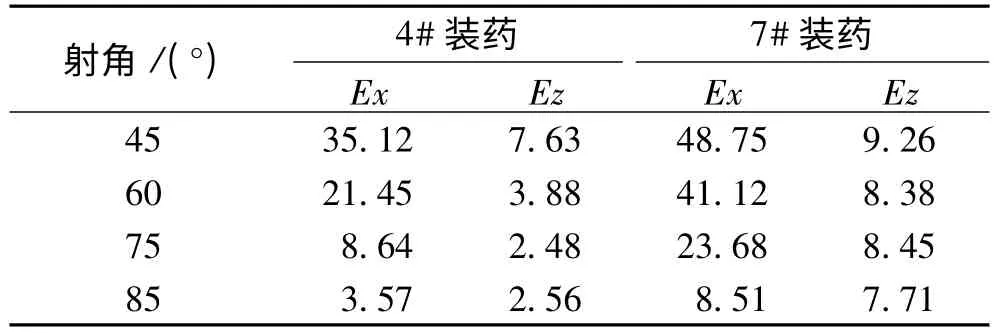
表5 对比弹概率误差Ex、Ez m

因为战技指标要求两弹弹道基本一致，可取α=0.01，λsp=0.6554。将 λsp、Ex、Ez代入式(1)，计算出新弹射程和方向的一致性设计控制限Kx、Kz，见表6。绘制K-θ曲线(描述一致性设计控制限随射角变化的趋势)，见图 7、图 8。

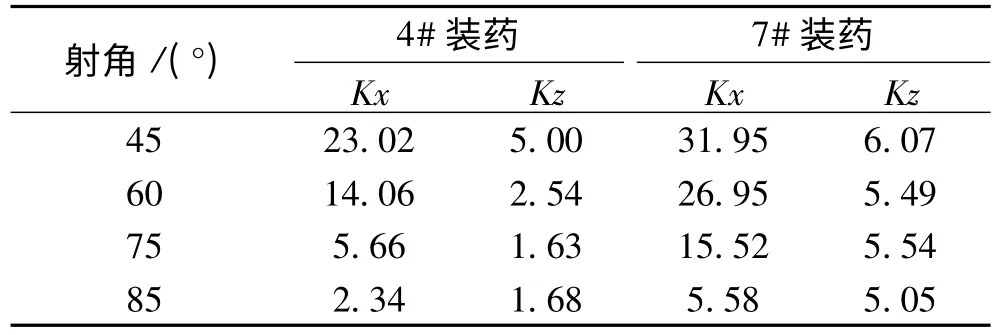
表6 新弹一致性设计控制限Kx、Kz m

图5 对比弹4#装药E-θ 曲线

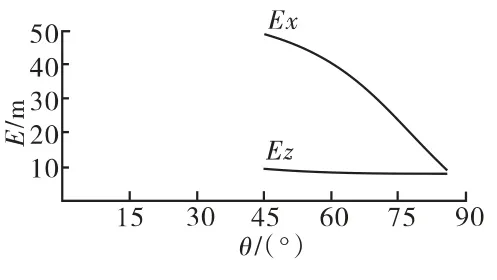
图6 对比弹7#装药E-θ 曲线

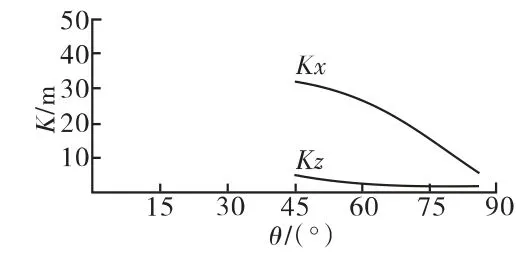
图7 新弹4#装药K-θ 曲线

图8 新弹7#装药K-θ 曲线

3.5 计算弹道差

a.估算新弹的阻力系数:新弹与对比弹几何外形相似，采用相同的引信和尾翼稳定装置，主要的阻力变化因素来自弹头部，因此其阻力系数可按式(2)估算(若有其它阻力变化，可在公式中叠加)。

根据文献[5]，定心部引起的阻力系数CxH按式(3)计算，并查图取ΔCxH值。

已知设计值H=1mm，D=82mm，代入式(2)、式(3)，计算出新弹的阻力系数，见表7。

表7 新弹的阻力系数Cx1(M)计算值

b.推算新弹的等效弹形系数:根据外道弹学中关于弹形系数的定义可知:

Cx0(M)、i'43d、Cx1(M)分别查表 3、表 4、表 7 取值，代入式(4)，计算出新弹的等效弹形系数 i'43，见表8。

表8 新弹的等效弹形系数i'43

c.估算平均弹道差:将初速、射角、弹重、等效弹形系数等代入外弹道计算程序，分别计算新弹和对比弹的平均射程 x－1、x－0以及平均弹道差 Δx－，见表 9、表10。绘制 Δx－-θ曲线(平均弹道差随射角变化的趋势)，见图 9、图 10。

表9 新弹4#装药弹道一致性理论设计数据

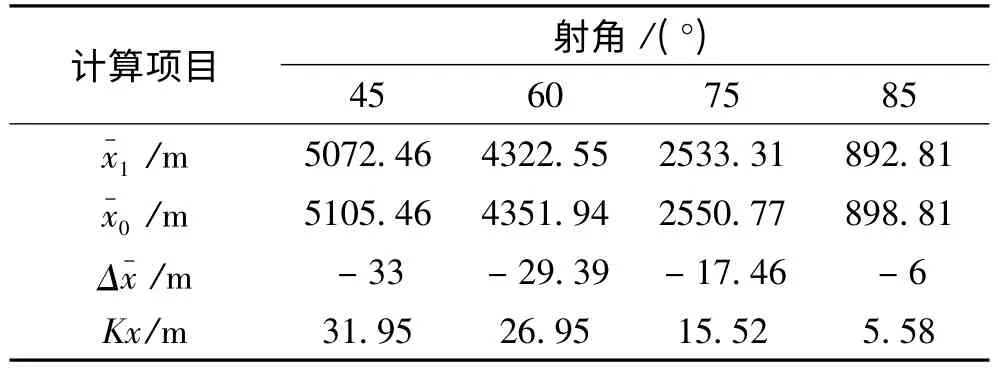
表10 新弹7#装药弹道一致性理论设计数据

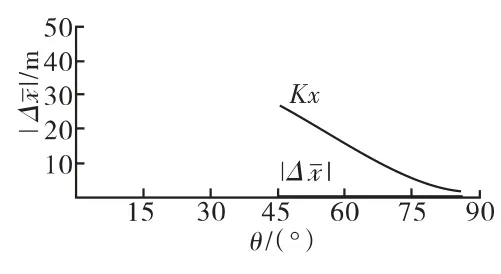
图9 新弹4#装药K-θ 曲线

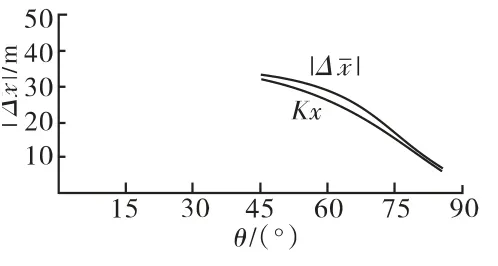
图10 新弹7#装药K-θ 曲线

3.6 初步设计结论

因为迫击炮弹的方向偏差较小，通常能满足要求，文中计算略。

由图9可知:4#装药的设计弹道差小于一致性设计控制限，可满足弹道一致性要求;同理，计算5#、6#装药设计弹道差，也能满足要求。

由图10可知:7#装药的设计弹道差大于一致性设计控制限，不满足弹道一致性要求。

3.7 改进设计

根据表10可知:新弹7#装药最大设计射程偏近，导致设计弹道差偏大。分析认为，主要原因是弹头部阻力较大。现将弹头圆柱部与定心部半径差H=1mm改为H=0.4mm，再按3.5节计算、制表并制图。经计算，4#、5#和6#装药满足要求，7#装药也满足要求，7#装药的计算结果见表11、图11。

表11 新弹7#装药弹道一致性理论设计数据

4 试验验证

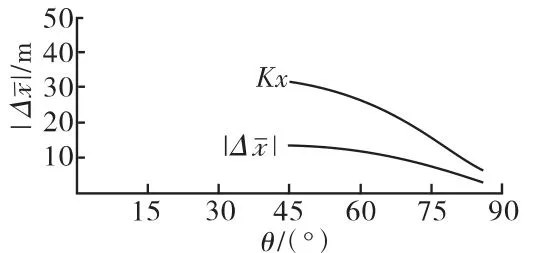
图11 7#装药曲线

以 7#装药、45°射角，结合最大地面射程及密集度试验进行了弹道一致性摸底试验，按文献[2]成对交叉检验要求进行试验和数据处理，见表 12、表 13。

由表13可知:对应于7#装药45°射角，新弹与对比弹弹道一致。7#装药其它射角和装药号的弹道一致性，在后续研制阶段得到验证，符合要求。

表12 射程和方向试验数据

表13 试验数据处理结果

5 结论

针对迫击炮弹，基于弹箭弹道一致性检验原理和方法，在设计保证内弹道一致的条件下，运用成对交叉检验法，通过外弹道计算，使新弹与对比弹的设计弹道差小于一致性设计控制限，理论上可以保证两弹弹道一致。在设计例证中，引入等效弹形系数的外弹道计算方法简单有效，符合性好。试验验证结果表明，所阐述的设计控制方法合理有效，有一定的实用价值。

[1]王中原，张领科.弹箭通用射表及弹道一致性检验方法[M].北京:科学出版社，2008.

[2]GJB 4225－2001榴弹定型试验规程[S].北京:总装备部军标出版发行部，2001.

[3]WJ 2144－1993弹道一致性设计与检验评定[S].北京:中国兵器标准化研究所，1993.

[4]魏惠之，朱鹤松，汪东晖，等.弹丸设计理论[M].北京:国防工业出版社，1985.

[5]臧国才，李树常.弹箭空气动力学[M].北京:兵器工业出版社，1989.