基于自适应A*算法和改进遗传算法的反舰导弹航路规划*

李红亮，宋贵宝，刘 铁

(海军航空工程学院，山东烟台 264001)

0 引言

航路规划的主要目的就是在确保飞行器安全飞行的基础上，以可实现的最优路径飞向目标。针对航路规划的求解，国内外学者已经做了大量的工作，比较成熟的算法主要有:动态规划法[1]、A*搜索法[2]、人工势场法[3]、遗传算法[4]、蚁群算法[5]、粒子群算法[6]等。但是这些搜索算法本身计算量比较大，计算时间也比较长，算法的研究大多只限于理论上论证技术的可行性，难于在工程上实现。为此，文中提出两种路径规划改进算法:自适应A*算法和改进遗传算法，主要目的是为了最大限度的减少计算时间，且不退化解的次最优性。

航路规划算法通常在所有可通行区域寻找全局最优路径，如果搜索空间不能涵盖全部可通行地区，该算法在搜索结束时可能会得不到全局最优轨迹[7]。文中提出的基于自适应的改进A*算法，解决了网络在搜索时间内无法覆盖所有可通行区域的难题，算法通过启发式的搜索更大跨度的区间，降低了错过最优解的可能性和缩短了收敛时间。经过改进的A*算法在搜索过程中根据当前作战区域的复杂性而自适应的改变搜索参数，克服了运算时间和搜索空间巨大的难题。此外，为了防止算法搜索不必要的战场区域，搜索空间是在搜索时智能产生的。搜索空间树从发射平台开始构造一直延伸到目标，延伸过程中考虑战场地理环境、导弹机动性能和动力航程约束。

近年来，遗传算法同A*算法一样，被广泛应用于解决复杂的优化问题。在路径规划问题，特别是在机器人应用技术中，顶点启发式方法被主要用于染色体创建，原因是最短路径必须通过起始点和目标点之间的所有障碍顶点。这个假设缩短了遗传算法的收敛时间，因为它只需搜索顶点，而不用搜索整个环境[8]。然而，对于反舰导弹航路规划问题，作战区域中的圆形威胁区没有任何顶点，并且地理海岸线非常复杂，只能由众多给定顶点代表。因此，顶点搜索不是一个有效的方法。文中提出一种新技术，可以在很短的时间内创建出可行的初始航路种群，且保持群体的多样性，算法从一个可行的种群入手，不再需要花时间来获得可行的个体。对于航路的编码，传统方式是采用固定长度的二进制字符串，这种编码方式对于含有障碍的搜索空间是非常困难的，进而导致了遗传进化速度的降低[9]。文中利用可变长度和实数编码技术，替代限定长度的染色体固化编码方式，提高了进化算法的灵活性。

1 约束定义和环境模型

反舰导弹向目标飞行过程中，需要避开某些特殊的区域，如岛屿、敌方火力拦截区、已方兵力集结区等，这些区域统称为飞行规避区，而反舰导弹的航路是要尽量避免与飞行规避区相交的。

飞行规避区半径是目标类型和速度的函数。例如，小目标有更好的机动性，因此未知的运动范围比大目标的要大。另外，航路规划时应该在飞行规避区边界设置一定的缓冲区，即将规避区边界适当外扩以修正反舰导弹的中段制导误差和风的影响。由于导弹飞行误差随时间的积累，缓冲区的半径随着导弹射距的增加而变大。

反舰导弹飞行规避区如图1所示，它是由网格组成的数字地图，网格的分辨率应根据导弹的最大射程或搜索算法所需的精度确定。每个网格的值为1或0，1表明在安全飞行区，0则表明在飞行规避区。文中提出的改进A*搜索算法和改进遗传搜索算法都是立足于数字规避地图，从目标到发射平台反向进行搜索的。反向搜索的原因是反舰导弹雷达开机时的目标距离和攻击舷角是非常重要的，它们直接决定了对目标的搜捕成功概率，因此必须首先确定。

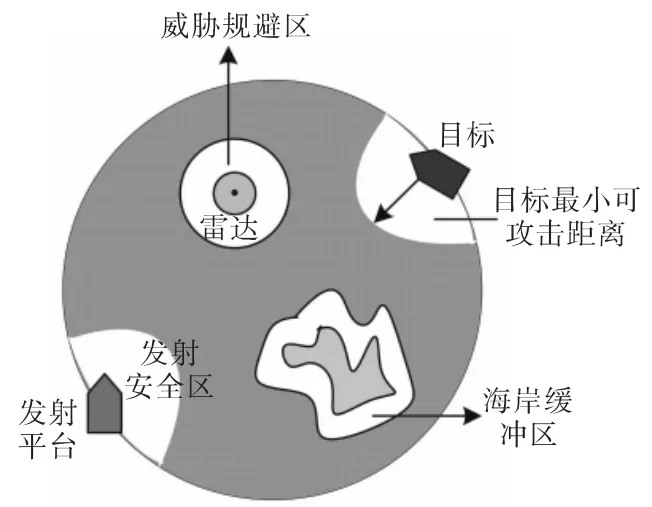
图1 反舰导弹飞行规避区数字地图

2 航路规划的改进A*算法

2.1 A*算法的基本原理

A*算法采用最佳优先搜索策略，从一个给定的初始节点到目标节点找到代价最低的航路[2]。它使用距离加代价的启发式函数来确定其搜索树中节点访问的顺序。距离加代价的启发式函数是两个函数之和:

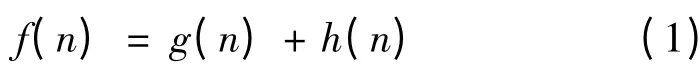
式中:g(n)为实际代价函数，表示从起始节点到当前节点的代价;h(n)为可接受的从当前节点到目标距离的启发估计代价函数，即其不能高估到目标的距离，对于反舰导弹航路规划而言，h(n)代表到目标的直线距离。其中:

式中:r(s，c)表示从起点S到当前节点C的直线距离总和;m(s，c)表示从起点S到当前节点C所需的全部机动距离之和;wr和wm分别表示直线距离和机动距离的权重，权重的大小直接影响航路规划结果，取决于决策者选择最小的航路长度还是最平滑的航迹。

图2 搜索扇面示意图

2.2 改进A*算法

A*搜索方法在构建网络时主要涉及3个参数。如图2所示，一个是搜索扇面角(2α)，另一个是角分辨率(β)或扇区角，最后一个参数是步长(L)，即当前节点与父节点之间的距离。搜索扇面角由反舰导弹的最大转弯角决定，它可以取最大转弯角的2倍。导弹在不超过最大转弯角时可以向右转或向左转。设置的扇面角越大，搜索的区域越大，意味着计算量越大。另外，角分辨率越小，找到最优解的概率就越大。然而，随着扇面角的增大或角分辨率的减小，收敛计算所需的内存和时间也成指数增长。步长受限于最小节点间距，即航路在相邻两次转弯之间的导弹飞行的最小直线距离。

综上所述，每个搜索参数对生成的航路和算法的收敛时间都有很大影响。传统的A*算法在确定搜索参数时没有考虑任务场景，使用默认值。当然也有些文献[10－11]，根据战术态势和作战场景，利用智能方法确定搜索参数，首先针对不同的任务场景估计得到不同的预计值，然后将这些值作为参数用于整个搜索过程，相比在每个场景使用统一的默认值，这样做的确减少了计算量。然而，对于复杂的作战场景，整个搜索过程仍过于缓慢，导致在一定的时间内无法获得最优解或次优解。

文中提出的改进A*算法，在搜索过程中，根据作战区域的复杂程度，自适应的调整搜索参数。例如，在简单的地理环境或障碍较少的情况下，可以降低搜索精度(粗搜索)以争取时间;当在复杂的作战区域，即搜索有难度或在飞行规避区有较少的可通行区域，则需提高搜索精度(细搜索)，以免错过理想的可行航路。

如图3所示复杂场景下的航路规划，搜索的早期阶段(作战区的上半部分)，由于环境不复杂，所以搜索分辨率设置得较低;但是在作战区的中间区域，反舰导弹飞行规避区域明显密集起来，可行通道较为狭窄，因此必须提高搜索分辨率细化搜索。虚线表示搜索参数为默认值时的搜索合成路径，点划线表示自适应调整搜索参数时的搜索合成路径，结果为虚线航路比点划线航路长得多。

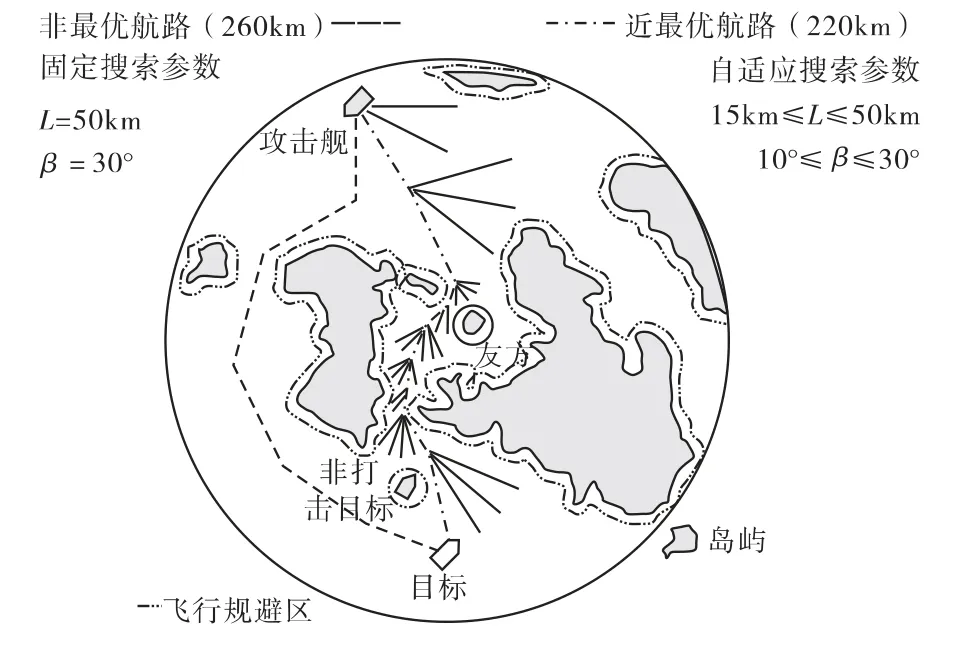
图3 固定与变化搜索参数时的航路对比

对于参数保持不变的A*搜索算法，要获得更好的航路，唯一的办法就是提高搜索分辨率。可是密集搜索就意味着高计算量。如图4所示，减小步长和扇区角，即提高分辨率，虽然能够获得更短的航路，但收敛计算时间成指数增长。而用自适应变搜索参数代替高分辨率，同样可以得到高质量的航路，但计算时间却大大减少(超过3倍)。

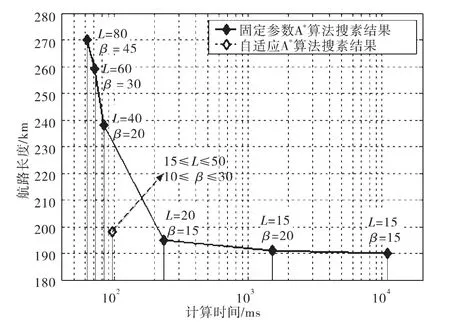
图4 分辨率对航路长度和计算时间的影响

改进A*算法的步骤概括如下:

1)以目标为起点，找到所有可能通向目标且相互不交叉的航路段，航路段长度等于反舰导弹对目标的最小可攻击距离。计算所有航路段的代价，将代价最小的放进CLOSE表中，其他的放进OPEN表中。

2)设置扇面搜索参数，使分辨率参数为最小(L=Lmax且 β = βmax)。

3)在OPEN表中找到最小代价的航路，在该航路末端利用搜索参数(L和β)创建一个搜索扇面，扇面角为反舰导弹最大转弯角α的2倍。将OPEN表中最小代价的航路放进CLOSE表中。

4)检查步骤3)中产生的航路避障情况。如果有任何航路与飞行规避区相交，则转步骤5);否则，转步骤6)。

5)将分辨率提高n倍(L=L/n且β=β/n)，但必须确保L≥Lmin且β≥βmin;另外，删除交叉的航路，把剩余航路放到OPEN表中。然后，转步骤3)。

6)将生成的航路放入OPEN表中。

7)将代价最小的航路放入CLOSE表中，新生成航路的“父节点”航路放入OPEN表中，目的就是可在OPEN表中追踪到任何一段航路的父节点航路。转步骤3)。

8)重复上述步骤，(a)直到发射平台与OPEN表中当前航路之间没有任何障碍，(b)直到OPEN列表是空的。

9)如果情况是(a)，意味着有解，可通过追踪OPEN表中当前航路的父节点航路找出一条合成航路。

10)如果情况是(b)，则意味着无解。

最后，为了缩短通过改进A*方法搜到的航路长度，采用航路拉直的方法，并尝试在合成航路上删除多余的航路点。

3 航路规划的改进遗传算法

将遗传算法应用于反舰导弹航路规划问题，关键是如何采用合适的编码方式对代表导弹飞行航路的染色体进行编码，如何在规定的约束条件下，不但要规避障碍保证导弹飞行安全，而且尽量最小化航路长度和平滑飞行轨迹。下面是文中提出的一种用于遗传算法的子算法。

3.1 编码方法和适应度函数

一条染色体表示航路点的一个序列。同时，为了使算法更加灵活，文中提出变长实数编码方法。这就是说，航路点的数量从一条航路到另一条航路可能是变化的，当然每条航路转弯点的数量不会超过反舰导弹自身性能所允许的最大航路点个数。

同A*算法中描述的代价函数一样，适应度函数由各航路点间直线距离总和与导弹机动距离总和加权组成。由于所有的备选航路都是可行的，适应度函数中不含惩罚项。

3.2 初始化种群

传统的遗传算法在初始化种群时，一般采用随机化的生成方式，这样做的好处在于它提供了解的广泛的多样性，但也存在不利之处。因为在作战区域可能会有许多障碍，初始化种群时随机选择的航路也许会穿越障碍，那么这条航路是不可行的。遗传算法从含有非可行解的初始种群开始搜索，意味着需要花费一些时间通过使用随机交叉和变异操作来获得可行的候选航迹。总体来说，可行候选解的搜索需要花费较长时间，降低了遗传算法的整体收敛性能。遗传算法采用随机产生初始种群的文献案例很多，例如文献[8]中的移动机器人路径规划研究。在该研究中，环境2的复杂程度与文中图5中的任务环境非常相似，结果显示在环境2中第一次可行的路径，是在第23代搜索到的，耗时2.59s。这对于反舰导弹作战需要实时任务规划而言是不可接受的，无法应用于工程实践。

另一方面，文中提出的新技术，可以在合理的较短时间内生成可行的初始航路群，遗传算法的收敛性能得到较大提高。然而，采用新技术替代随机生成初始种群也是以损失种群的多样性为代价的。为此，新技术在生成初始可行候选解时，加入随机因素来保持搜索空间的多样性和广泛性，并采用了基于简单树的搜索算法。算法主要步骤如下:

1)设置起始点为当前节点。

2)在当前节点利用分辨率参数(L和β)创建一个搜索扇面，扇面角为反舰导弹最大转弯角α的2倍，设为一固定值。

3)检查当前产生的扇面内的每段航路的避障情况，删除与飞行规避区相交的航路。

4)产生一个随机整数r，1≤r≤nw+1，这里nw为反舰导弹最大航路转弯点个数。

5)检查随机分配因子是否小于等于扇面边数。如果r≤ nl，转步骤6);否则转步骤7)。

6)随机选择扇面中的一条边，然后转步骤2)。这意味着航路段应该随机产生，直到r＞nl，这么做保证了初始可行解的多样性，并防止了搜索容易陷入局部极小点。

7)计算扇面内各航路末端到目标的直线距离，选择距离最小的边以替代随机选择，然后转步骤2)。参数r决定了何时停止随机式选择、启用确定式选择。随机式选择帮助增加了解的多样性，而确定式选择引导航路指向目标。例如，如果r较大，获得的初始航路会较长、较弯曲，但维护了解的多样性;此外，一旦缩小r值，就会获得更短、更平滑的航路。这对于改进遗传算法的收敛效率是有用的。

8)为了获得一条可行的候选航路，重复步骤2)～7)，直到当前节点与目标节点之间没有障碍。

如图5所示，利用提出的初始解产生方法，在0.37s这么短的时间内就生成了20条可行航路，并且初始种群覆盖了图5障碍环境中绝大多数的可通行区域，解的多样性是令人满意的。还有就是改进遗传算法搜索效率也是很高的，在第32代便获得最优解，收敛耗时 1.03s。

3.3 遗传操作

1)交叉算子。将种群两两组对，采用单点交叉法对每组染色体实施交叉操作，两个父代染色体随机生成要相互交叉的节点位置，交叉操作后，父代航路用直线在选择的交叉点处连成两条新的子代航路(如图6所示)。如果连线与作战区域的障碍相交，采用修正算子将其修复成可行航路。

图5 种群初始化

图6 遗传操作示意图

2)变异算子。随机选择航路某一节点，将该节点转变到另一位置，生成一条新的航路，实现对航路的变异操作(如图6所示)。变异会不断重复操作过程，直到获得可行的子代航路。

3)修正算子。修正算子仅用于支持交叉和变异算子，并不单独使用。染色体在进行交叉和变异操作后，如果获得的解为非可行解，它可以通过修正操作将非可行解变得可行。文中在使用遗传算法进行反舰导弹航路规划时，没有采用伸展机制来平滑候选航路，目的是不减少搜索的多样性，避免搜索过程陷入局部极小点。

4 仿真结果和分析

利用改进A*算法和改进遗传算法分别对3个不同复杂程度的作战场景进行仿真实验，并且对仿真结果进行比较和分析。

如图7中显示的3个地理场景，作战区域网格大小为100m×100m，复杂等级从1到3，衡量标准为障碍数量的多少，改进遗传算法交叉概率C取0.5，变异概率M取0.2，种群规模PopSize取20。表1给出了仿真结果，包括两种改进算法在3个想定中的搜索收敛时间和航路距离。根据仿真结果，改进遗传算法的收敛时间随环境复杂程度的提高而增长，而改进A*算法并没有明显变化，表明改进A*算法在搜索过程中通过自适应调整搜索参数能适应不同的作战环境。改进A*算法随环境的变化，收敛时间不仅未受到实质影响，而且由于运算时间短，能够满足实时航路规划要求。虽然改进遗传算法在收敛时间上落后A*算法10倍以上，但其收敛精度更高，能获得最优解(如场景2中航路比改进A*算法缩短了15%)

图7 仿真结果图

在场景1和场景2中，除了遗传算法压缩了A*找到的路径，使之变短了一些之外，两种算法发现的路径十分相似。然而，在场景3中，两种算法获得了航路总长差别很小却截然不同的路径。A*算法不能获得遗传算法所发现的可通行区域的原因可能是自适应搜索参数间隔大小的问题。通过提高角分辨率β或减小搜索步长L，可以获得更好的路径。出于该目的，β和L的间隔被缩短到极限，仿真结果表明提高搜索分辨率使A*算法获得了同遗传算法所得结果相似的航路。虽然如此，A*算法获得的航路仍然比遗传算法发现的航路长4.8km之多，这意味着分辨率还是不够。然而提高分辨率会让A*算法的搜索计算时间成指数增长。

表1 仿真结果

5 结束语

航路规划计算的主要难题在于运算时间长、消耗内存大。为了提高运算速度，文中提出了分别基于A*算法和遗传算法的两种不同的规划技术，用于反舰导弹航路规划。仿真结果发现，通过提高传统A*算法的适应性和将种群智能创建技术加入传统遗传算法，时间收敛均显著降低，而且不会恶化解的收敛精度。两种改进方法彼此各有优缺点，比较表明在计算时间上改进A*算法要优于改进遗传算法，但在解的最优性上则落后于后者。所以，改进A*算法适合用于时间要求苛刻，尤其是动态环境中需要紧急规划的任务问题;相反，改进遗传算法则适合用于发射前并且精度要求高的航路规划问题。

文中主要研究的是单导弹航路规划，两种改进算法可以扩展用于多导弹协同航路规划问题，可以通过并行运算、相互通信、彼此协调共同完成多重航路规划研究，这是后续研究的内容。

[1]郝峰，刘明喜，翟英存，等.动态规划算法在巡飞弹航路离线规划中的应用[J].弹箭与制导学报，2007，27(1):67－69.

[2]张雅妮，高金源.一种基于改进A*算法的三维航迹规划方法[J].飞行力学，2008，26(1):48－51.

[3]徐肖豪，李成功，赵嶷飞，等.基于人工势场算法的改航路径规划[J].交通运输工程学报，2009，9(6):64 －68.

[4]X Zhao，X Fan.A method based on genetic algorithm for anti-ship missile path planning[C]//Proc.of the IEEE Int.Joint Conference on Computational Sciences and Optimization，2009:156－159.

[5]孙涛，谢晓方，乔勇军.基于二维自由空间蚁群算法的反舰导弹航路规划仿真[J].系统仿真学报，2008，20(13):3586－3588.

[6]于会，于鑫，李伟华.基于粒子群优化算法的航迹规划与重规划[J].计算机工程，2009，35(15):206－208.

[7]D Xin，C Hua-Hua，G Wei-kang.Neural network and genetic algorithm based global path planning in a static environment[J].Journal of Zhejiang University Science，2005，6(6):549－554.

[8]Y Wang，D Mulvaney，I Sillitoe.Genetic-based mobile robot path planning using vertex heuristics[C]//Proc.of the IEEE CIS，2006:1－6.

[9]Y Wang，D Mulvaney，I Sillitoe，et al.Robot navigation by waypoints[J].Journal of Intelligent and Robotic Systems，2008，52(2):175 －207.

[10]R J Szczerba，P Galkowski，I S Glickstein，et al.Robust algorithm for real-time route planning[J].IEEE Transactions on Aerospace and Electronic Systems，2000，36(3):869－878.

[11]K Tulum，U Durak，S K Ider.Situation aware UAV mission route planning[C]//IEEE Aerospace Conference，2009:1－12.