基于DSP的火箭炮神经网络PID位置控制器的设计*

翟小晶，马大为，乐贵高，孙 德

(南京理工大学机械工程学院，南京 210094)

0 引言

某防空多管火箭炮发射架由方位和俯仰伺服系统组成，发射架的控制精度对火箭炮的打击精度有着重要的影响。传统PID控制器缺点是参数固定难以在存在非线性的系统下获得良好的动静态特性。文献[1]提出采用模糊控制器，但是其缺点是因模糊控制器缺少积分作用会出现稳态误差，且单纯使用模糊控制器应用于一个高精度的位置伺服系统，往往会出现系统的动态特性难以被精确控制的问题;文献[2]提出采用滑模控制器提高系统对参数时变、外部干扰的抵抗力，增强系统的鲁棒性，但是滑模控制器缺点是其开关特性使系统存在“抖动”的缺点，难以直接在实际系统中应用。文中利用神经网络具有很强的自学习、自适应和非线性系统逼近能力的优点，将其与PID控制器结合，动态的改变PID控制器参数以提高控制器的自适应能力[3－4]。

文中利用Matlab软件完成了神经网络的离线训练，鉴于神经网络运算量大难以满足实时性运算的缺点对神经网络进行了适当的简化，通过TI公司的TMS320F2812型DSP处理器实现了样机的在线控制。多管火箭炮发射架交流伺服系统结构简图如图1所示。

1 发射架位置控制器设计

1.1 RBF神经网络简介

神经网络是对人脑结构的模拟，已经证明三层前馈神经网络可以以任意精度逼近非线性系统。径向基神经网络(RBF)是一种隐节点采用径向基函数包含输入层、隐层、输出层的三层前馈神经网络，其径向基函数神经元的活跃程度与输入距神经元的距离成反比，从而使整个RBF网络呈现局部特性。这使得对应于每个输入只需要调整几个相关的网络权值，从而使整个网络具有较快的收敛能力。RBF神经网络结构如图2所示。

图1 火箭炮发射架交流伺服系统结构简图

图2 神经网络结构图

隐节点输出为:

网络输出为:

其中，Cj= [cj1，…，cji，…，cjn]T为网络的中心矢量，i=1，2…，n;B= [b1，…，bm]T为网络的基宽常量;W= [w1，w2，…，wj，…，wm]T为网络的权值。

1.2 神经网络控制器的设计

文中设计的PID控制器采用RBF神经网络来辨识被控系统以实时调节PID控制器的参数，其结构简图如图3所示。

图3 火箭炮发射架位置控制器简图

其中:PLANT为伺服驱动器、永磁交流伺服电动机与减速器。

系统的给定信号为系统输入与系统输出之差，即:e(t)=r(t)－y(t)。

则控制器输出为:

其中:

xc(1)=e(t)是系统的跟踪误差;

xc(3)=∫e(t)是系统跟踪误差对时间的积分。

取神经网络的整定指标:

kp、kd、ki的调整采用梯度下降法:

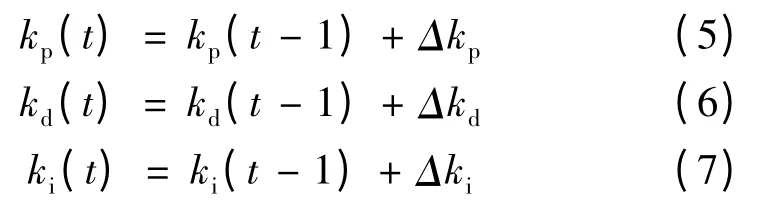
其中:

式中:α、β、γ 为 △kp、△kd、△ki的调节参数，δy/δu 通过神经网络NNI辨识。文中取α = －1.7，β = －0.001，γ = － 0.002。

当PID控制器控制参数取较大值时容易引起系统的振荡，故取:

8 ≤ kp≤15;0.15 ≤ kd≤0.25;0.01 ≤ki≤0.015

1.3 神经网络离线训练

神经网络辨识器是利用上一时刻的输入输出来辨识被控系统当前时刻的输出，取网络输入输出向量:X= [u_1，y_1]

Y=y其中，u_1，y_1为上一时刻速度环电压输入值、系统输出;y为当前时刻系统输出。上述离线样本是在单纯PID控制器作用时由CCS软件采集，系统离线训练的过程由Matlab软件完成。

神经网络的层数、神经元个数及位置对网络的性能有着重要的影响，传统的离线训练算法包括梯度下降法、聚类算法等都存在着网络的层数和个数事先经人为确定就不能改变的缺点，文中采用改进的动态资源分配网络算法，其能够自动增减网络隐节点的个数。设离线样本为[A，B]，算法如下[5]:

1)网络的初始隐节点为第一个样本点，取网络分辨率 α =αmax。

2)计算误差‖Ei‖ =‖yi－f(Ai)‖，其中yi为系统采样的输出值，f(Ai)为网络输出。同时，计算样本与已存在隐节点的最小距离:

3)计算新输入样本点是否满足误差准则和距离准则，即‖E‖ ＞ε和d＞αi(ε为网络期望精度，αi=max(αmaxλi，αmin)，αi为网络在第i个输入时要求的拟合精度，0＜λ＜1，即随着输入样本的增加希望网络的拟合精度越来越高)，如满足则分配新的隐节点，其新增加隐节点参数为:

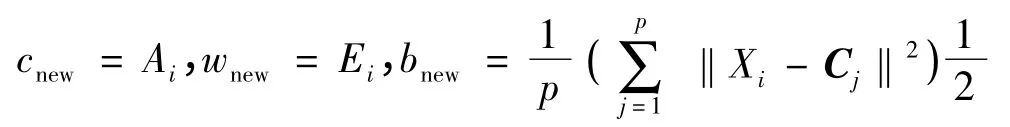
否则直接使用梯度下降法调节网络的权值、中心点及扩展常数。

5)重新输入一个新样本，转到步骤2)。

1.4 神经网络在线训练算法

神经网络在线训练的目的是为了增强网络的自适应性，弥补离线训练过程中由于样本不完整性及离线训练算法选择不当带来的缺点，文中选用梯度下降法来在线调整神经网络的参数。

定义神经网络性能指标函数:

可得到输出权值、节点基宽参数及节点中心矢量的迭代算法如下:

式中:η为学习速率，α为动量因子。

1.5 神经网络在DSP中的实现

虽然RBF神经网络相比较其它网络具有结构简单、计算量小的优点，但隐含层层数、隐节点个数增加均会造成运算量成倍增加，如直接进行运算处理，处理器的处理速度达不到实时控制的要求[6]。

DSP处理器的优点是采用了流水线乘加运算技术，每个指令周期都能够操作多个乘加指令，因此将神经网络复杂的逻辑运算转换为乘加运算指令，是解决神经网络因运算量大不能满足实时性要求的有效途径。

Iq mathLibrary是TI公司经过优化的，能够在定点DSPTMS320C28XX上实现精确浮点运算的数学库函数，使用这些库函数可以明显提高运算的速度，而且可以得到更高的精度。

Iq math Library中，命令_IQN(x)意思是将x转换为具有2－N精度的浮点型常量;命令_IQNtoF(x)意思是将_IQ格式数据转换为浮点型数据;_IQNmpy(_iqN A，_iqN B)是以2－N为精度进行乘法运算。以下例为例实现浮点型乘法运算:C=A×B;

Float A B C//定义浮点型变量

A_iq=_IQ29(A);B_iq=_IQ29(B);//将浮点型变量转化为_iq型变量

C_iq=_IQ29mpy(A_iq，B_iq);//乘法运算

C=_IQ29toF(C_iq);//将_iq型变量转化为浮点型变量

RBF神经网络隐节点中采用的函数是高斯函数，隐层输出是e的非正整数幂的乘加运算，如果直接采用Iq math库中的POW()函数进行运算，其运算周期较长，不能满足实时性的要求，可以通过泰勒公式将其展开:

所取的项数根据要求的运算精度来进行确定，而欧几里得泛数和幂运算可以由乘法运算来进行替代，采用乘加运算可以大幅提高运算速度。

2 实验

以方位伺服系统为例，方位方向减速器减速比为1/192，方位电机参数为:折算到电机输出轴的转动惯量:J=8.625 × 10－3kg·m2;燃气流冲击力矩及未建模动态干扰为:T=10N·m;定子电阻R=2.6Ω;绕组电感:Ld=Lq=50 ×10－3H;额定电流Ie=6.4A;容许最大电流Imax=12.8A;磁极对数Pn=4;电磁转矩系数 kc=1.11N·m/A;阻尼系数B=1.43 ×10－4N·m·s;电机额定转速:n=2000r/min，采样时间间隔t=20ms。

取阶跃信号输入值:r(t)=60;

正弦输入信号为:r(t)=75sin(0.7136t);

可得实验跟踪误差曲线如图4所示。

由图4、图5知，采用神经网络PID控制器可以有效的提高系统的响应速度，增强系统的抗负载能力;由图6、图7知系统在稳态跟踪时由于控制器的参数可以动态的改变，可以有效的提高系统的跟踪速度。

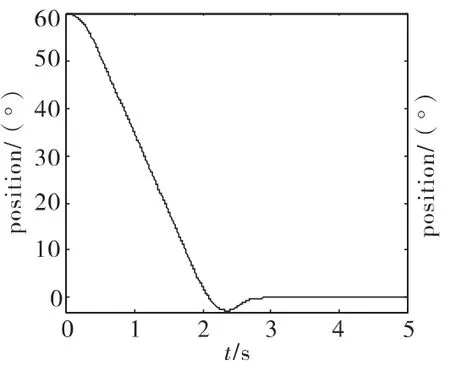
图4 PID控制器满载阶跃误差曲线

图5 复合控制器满载阶跃误差曲线

图6 PID控制器满载正弦跟踪误差曲线

3 结论

传统PID控制器难以满足多管火箭炮在跟踪精度、响应速度及抗负载能力方面的要求，文中利用神经网络的自学习、自适应能力将其与PID控制器相结合弥补了PID控制器因参数固定带来的缺点，并通过简化神经网络将其成功的应用于DSP数字信号处理器。实验结果表明此控制器相较于单纯PID控制器可以有效的提高系统的动态性能。

[1]张蔚.模糊神经控制算法在永磁同步电机控制中的应用研究[D].武汉:武汉理工大学，2004.

[2]郭亚军，马大为，王晓锋，等.反演控制在交流位置伺服系统中的应用[J].机床与液压，2011(1):74－76.

[3]文广，赵丁选，倪涛.新型力觉径向基神经网络整定PD控制算法研究[J].西安科技大学学报，2009，26(3):421－425.

[4]孙德，乐贵高，庄文许.火箭炮位置伺服系统的复合PID控制[J].弹箭与制导学报，2012，32(1):215－218.

[5]魏海坤.神经网络结构设计的理论与方法[M].北京:国防工业出版社，2005.

[6]胡健，马大为，郭亚军，等.基于DSP的防空火箭炮模糊神经网络位置控制器设计[J].测控技术，2010，29(9):35－39.